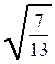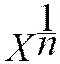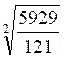COURS

RACINES D' UN NOMBRE  RELATIF :

I ) Nomenclature  :       Ecriture mathématique:

   Définition de l’objectif : Savoir « donner » le radical d’un nombre. ;    (On dit aussi donner la racine « carrée  ou cubique d’un nombre »)

a)  « Radical »

                Le mot « Radical » est le nom donné au signe :                

                Ce signe  est constitué d’un « vé » prolongé par une barre horizontale.(recouvrant totalement un nombre ou une opération ).

  Exemples  : 

  ;  ;  ;

b ) « Radicande »

Le nombre (ou opération)  situé sous la barre horizontale s’appelle : radicande

c ) Ce qui  gravite autour de ce  signe :

                                      la barre horizontale prolongeant le « vé » couvre la partie numérique(exemple  ; ici  25 est le radicande ).

sur la branche la plus courte du « vé » (à gauche) est inscrit un nombre ;  (qui  indique

le degré de la racine carré pour le nombre (2) ;cubique  pour le nombre (3) , ou quatrième pour le nombre  (4) ;ainsi de suite.........                  

La pointe du vé étant sur la ligne d’écriture.

CAS   GENERAL:  RACINE   n ^ième  d’un nombre et Puissance n ^ième    

                     La « racine » d’un nombre « X » est l’opération inverse de la puissance qui tend à trouver le nombre « x »de départ qui à permit de calculer  X .

                        en faisant     le calcul de     xⁿ   on obtient un nombre " X " ;                donc  inverse en  faisant le calcul  X^1/n    on retrouve le nombre " x"

       En ayant  « X »   est « n »  ;on demande de retrouver « x » ; pour cela on utilise l écriture

   =   x =

 ( sachant que l’on a admis    que     x ⁿ =X   )

Remarque: La racine  « n » est égale à la puissance inverse de « n ».

On écrit aussi que   :    =         ; ces deux écritures mathématiques ont la même signification;(Cette écriture est  utilisée  dans l'objectif « dérivation et intégration » .

 - Remarques :   les écritures   de la forme      ;telle que        et          sont souvent utilisées  sur les  calculatrices (pour effectuer la même opération ,cela dépend des marques ).

A savoir :

-S i   x ^y  = X   , alors  x   =  

               (traduction : si le nombre petit ixe  à la puissance y  a pour résultat ( est égal ) le nombre grand   ixe ,alors le nombre petit ixe est égal à la racine hi grec i^ème  du nombre grand ixe. )

Exercices les plus exécutés :

Commentaire:

il n’y a pas de difficulté à calculer  la puissance d’un nombre (x ^y );il n’en est pas de même pour calculer la racine n^ième d’un nombre :

Comment obtenir la valeur d’une racine  d’un nombre ?

Pour obtenir la racine n^ième d’ un nombre ( exemple :  ) il y a plusieurs possibilités:

  a)  soit par le calcul: Il est possible de calculer la racine carré d’un nombre; cela fait l’objet d’une leçon particulière.(c’est le seul cas de calcul qui peut être accessible à un élève). ( voir les logarithmes) .

  b)  Soit par identification: il faut connaître et donc reconnaître les carrés parfaits.

c)      Pour tous les autres cas il vous faut consulter une table numérique (recensant tous les calculs faits à l’avance )

 d)    ou alors il vous faut apprendre à utiliser la calculatrice.

Autres écritures  utilisées par les calculatrices:     signifiant que l’on calcule le radical d’un nombre.

a)            est  =   à       .  (que l’on traduit par « racine » y ^ième de X )

 b)          est  =  à          .  (que l’on traduit par « racine » x ^ième de  y )

RACINES D' UN NOMBRE  RELATIF

Deux cas renfermant deux cas  :

CONTROLE

Que signifie: calculer le radical d’un nombre ?

Donner l’écriture utilisée sur les calculatrices  pour effectuer la recherche d’un radical d’un nombre.

Quelles sont les possibilités d’obtenir la valeur numérique  de la racine n ^ième d’un nombre ?

Ecrire différemment  les expressions  suivantes :  (forme d'écriture : puissance )

EVALUATION:

Trouver les racines carrées parfaits des multiples de dix:

de 10⁰  à 10 ⁸

si elles existent ! pour  10⁰  ;10¹ ; 10² ;  10³ ;  10⁴  ; 10⁵ ; 10⁶  ;10 ⁷ ; 10 ^8;

Première série d ’exercices :

soit  un nombre « x » ; trouver la racine carrée du nombre :

x =0.25  ;  =

x = 7,29  ;  =

x = 33,64   ;  =

x = 81    ;  =

x = 291 600   ;  =

x = 2 744 000    ;  =

x = 1,574610⁸    ;  =

II  )Deuxième série d’exercices en relation avec la racine carrée  d’un produit:

=

 =

 =

 =

 =

 =

donc :  ==

III ) Troisième série d’exercices en relation avec  la racine d’un quotient:

Ces exercices utilisent des carrés parfaits

 =

 =

 =

Se ramener aux carrés parfaits; en se souvenant que tout nombre « à virgule » peut se mettre sous forme de fraction de dénominateur égal a ...........

=

  =

IV ) Quatrième série  d’exercices en relation avec la racine carrée d’une  addition ou d’une soustraction , et les transformations

  a)    =

   b )  =

    c ) =

    d  ) =

e ) =

f ) =

g ) =

h ) =

k ) =

V  ) Cinquième série d’exercices: Donner une valeur approchée d’une racine d’un nombre

1 ° ) Calculer les expressions  suivantes avec la précision du  dixième

 =

 =

 =

2 ° ) Calculer les expressions  suivantes avec la précision du  centième

 =

 =

 =

3 °) Calculer les expressions  suivantes avec la précision du millième

 =

 =

 =

 =

 =