|
2°) Puissances d’opérations simples. |
Objectif suivant : 2°) calcul algébrique : Produits (
niveau 4) |
|
|
|
ENVIRONNEMENT
|
Objectif précédent : 1°) Puissances
les carrés d’opérations simples 2°) Vue :
les Identités remarquables ( carrés d’un
somme ; carrée d’une différence) |
Objectif suivant : 1°) puissances et encadrement : 2°)
Puissances de dix et les opérations de base. 3°)
Puissances et racines niveau IV. 4°) calcul
algébrique : Produits ( niveau 4) |
|
|
DOSSIER niveau V : « PUISSANCE »
Partie 5/5 : Les puissances d ' opérations simples.
Produits et quotients de puissances
(exclues les sommes et différences : voir les identités
remarquables)
|
|
|
|
|
|
I )Transformation d’une Multiplication d’un même
nombre élevé à des puissances différentes: |
|
|
|
|
|
|
|
|
|
|
COURS |
Interdisciplinarité |
|
|
Info plus !! |
|
|
|
|
IV ) Transformation d’ une
Puissance d’une fraction:
![]() =
=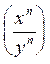
Lire : une fraction
« x » sur « y »
élevée à une puissance « n »
est égal à une fraction dont le
numérateur « x » est élevé à la puissance « n « et le
numérateur « y » élevé à la puissance « n ».
a)Applications
numériques:
![]() =
=![]()
![]()
![]()
![]()
![]() =
=![]()
b) Application
algébrique:
![]() =
=![]()
![]()
![]()
![]()
![]() =
=![]()
V )
Transformation d’une fraction dont la numérateur et le dénominateur sont de
même valeur mais de puissance.
(Voir les conditions pour « x »)
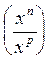 = x n-p
= x n-p
a) Application numérique:
Rappel
*x -1 = ![]() ; x -1 s’appelle
l’inverse de « x » ;donc x -p =
; x -1 s’appelle
l’inverse de « x » ;donc x -p = ![]()
![]() =
=
Procédure de
transformation: ![]() = ?
= ?
a) on transforme la fraction en multiplication : 32 ![]()
![]() =
=
b) On transforme l’écriture : ![]() en 3 -3
en 3 -3
c)On récrit la transformation sous forme
d’égalité: ![]() = 3(+2)
= 3(+2) ![]() 3 (-3)
3 (-3)
d)On applique
la transformation :x n ![]() x p = x n+p avec n = (+2) et p = (-3) ce qui donne
:
x p = x n+p avec n = (+2) et p = (-3) ce qui donne
:
3(+2) ![]() 3 (-3) = 3(+2)
+(-3)
3 (-3) = 3(+2)
+(-3)
e) On applique les règles de
l’addition de deux nombres relatifs (+2) +(-3)
= (-1),pour ce qui concerne les exposants.
pour ca
d) on rend compte: ![]() = 3(+2)
= 3(+2) ![]() 3 (-3) =
3(-1)
3 (-3) =
3(-1)
Conclusion: ![]() = 3(+2) -(+3)
=3(+2) +(-3) =3(-1)
= 3(+2) -(+3)
=3(+2) +(-3) =3(-1)
*si ![]() résultat de la
transformation : 32
résultat de la
transformation : 32
b) Application
algébrique:
*x -1 = ![]() ; x -1 s’appelle
l’inverse de « x » ;donc x -p =
; x -1 s’appelle
l’inverse de « x » ;donc x -p = ![]() et inversement x
p =
et inversement x
p = ![]()
Voir les deux cas :
Premier cas: « n » est > à « p »:
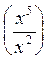 = x5
= x5 ![]()
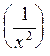 =x 5
=x 5![]() x -2= x
3
x -2= x
3
Deuxième cas « n » est <
« p »:
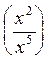 = x2
= x2 ![]()
![]() =x 2
=x 2![]() x -5= x-3
x -5= x-3
APPLICATION AUX PUISSANCES DE DIX :

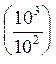 = 10 3-2 (=10)
= 10 3-2 (=10)

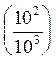 = 102-3 ( = 10-1)
= 102-3 ( = 10-1)
|
Applications : (Déjà traité : voir Objectif : QI 1b
) |
|
|
A ) |
|
|
B) |
|
IMPORTANT POUR EXPRIMER DES GRANDEURS EN SCIENCES /
PHYSIQUE.
Cette
application est utilisée en science pour rendre compte des unités ;d’un calcul:
exemple : l 1 / m 3 :lire des litres par mètre cube s’écrit aussi : l ![]() m -3
m -3
autre exemple: si l’on divise un volume par une distance (exprimés par exemple en mètre)
nous faisons m3 / m1 ce qui donne des m3-1 soit
des m2, le nombre obtenu par calcul représente le résultat d’une
surface.
Voir leçon en
sciences sur les calculs de longueur, surface, volumes ;et autres ........
RESUME à savoir "par
cœur"
|
|
|
x n |
|
x n |
|
|
|
(
X n )p = X
n |
|
|
|
|
TRAVAUX AUTO
FORMATIFS.
:
|
Transformer les
expressions suivantes |
résultat |
Val. |
|
|
|
|
|
x n |
|
|
|
X n |
|
|
|
|
|
|
|
( X n )p = |
|
|
|
X n |
|
|
|
x n+p = |
|
|
|
(
X
|
|
|
|
|
|
|
|
|
|
|
|
x -p = |
|
|
|
X n-p = |
|
|
|
|
|
|
Calculer
a) ( 8 ![]() 10-3 ) 2 =
10-3 ) 2 =
b)
( 23 ![]() 10-2 ) 2 =
10-2 ) 2 =
Pour chaque cas remplacer
x = 3 ; y =2 ; n =3 ; p=2
.et faire les transformations des expressions suivantes:
|
résultat |
remplacement |
Calcul
éventuel |
|
|
|
|
|
x n |
|
|
|
x n |
|
|
|
|
|
|
|
(
x n )p = x n |
|
|
|
x n |
|
|
|
x n+p = x n
|
|
|
|
(
x
|
|
|
|
|
|
|
|
|
|
|
|
x -p = |
|
|
|
X n-p = |
|
|
|
|
|
|
*
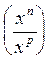 =
=![]() = 3(+2)
= 3(+2) ![]() 3 (-3) =
3(-1) ;
3 (-3) =
3(-1) ; ![]() = 3(+2) -(+3)
=3(+2) +(-3) =3(-1)
= 3(+2) -(+3)
=3(+2) +(-3) =3(-1)
I ) CALCULER SOS cours
|
10 3 = |
(+1)10 = |
(-1)7 = |
(-3)3 = |
|
10-5 = |
(-1)12 = |
(+2)-2 = |
( |
|
( |
( |
( |
( |
II)
Ecrire plus simplement: (niveau « seconde » )
|
(5a)2 |
a5
:a7 = |
3a4 |
a-3:a-5 |
|
14
a 2 b3 : 49 a3 b2 = |
|
|
(2ab)3
(3b)2= |
III ) Ecrire sous la forme an
avec n Î Z : SOS Cours : cliquez ici
C
= 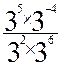 ; D =
; D = 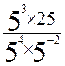 ; E = ( 23
)2
; E = ( 23
)2![]() 2
2
IV)
Ecrire sous forme décimale : SOS cours
|
375
|
21 |
3.4 |
0.04 |
|
21000 |
|
|
|
|
|
|
|
|
|
|
|
IV) Calculer
A à partir de l’expression suivante:
A = 2x3 +3x2 -x +7
pour a) x
= +1
pour b)
x = 0
pour c)
x = +0,1
pour d)
x = -1
pour e) x= 3
pour f) x= -2,8
VOIR FICHE UTILISATION DE LA CALCULATRICE
mso-bidi-font-size:10.0pt; font-family:Arial'>
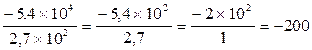
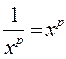
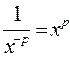
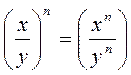
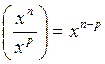
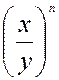
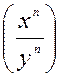
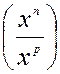
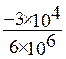 =
=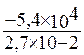 =
=