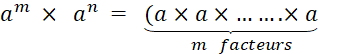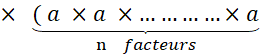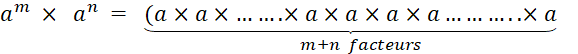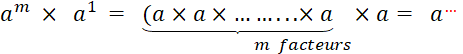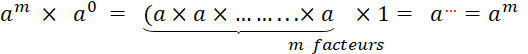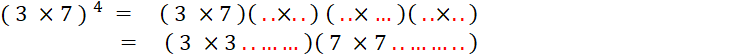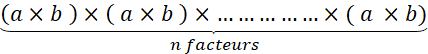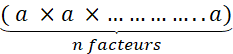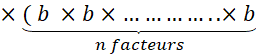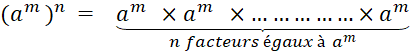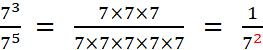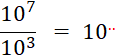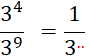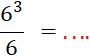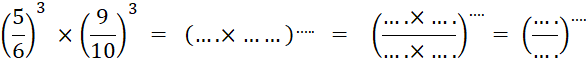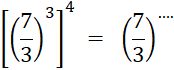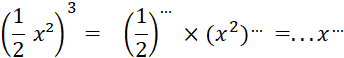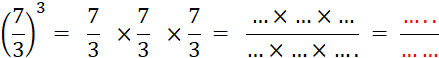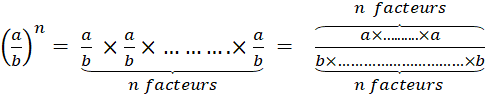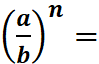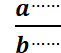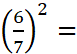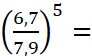Classe de quatrième collège.
			Programme classe de 4^ème
Pré requis:			Vers le corrigé
la multiplication de deux nombres entiers naturels	cliquer ici
la multiplication de deux nombres décimaux positifs:	cliquer ici
Puissance : écriture normalisée et indicée	Cliquer ici

ENVIRONNEMENT du dossier

Index warmaths

Objectif précédent 1°) la multiplication d’un nombre par lui - même 2°) voir le cours sur « comparaisons » et « carrés »

Objectif suivant 1°) le cube d’une nombre 2°) « Carré » d’opérations simples. ( + ; - ; ¸ ; ´ ) 2°) les Identités Remarquables 3°) les puissances Nièmes 4°) RACINE « CARRE » 5°) puissance des nombres relatifs 6°) « puissance de dix ». 7°)éventuellement voir le cas de la puissance de deux nombres positifs ou négatifs.

1°) Tableau 68 2°) table numérique Vers la liste des cours sur le calcul numérique

DOSSIER: PUISSANCES de nombres positifs

Fiche 1 : Puissance d’un entier ou d’un décimal positif.

Fiche 2 : Produit de puissances d’un même nombre.

Fiche 3 : Puissance d’un produit de décimaux positifs.

Fiche 4 : Puissance d’une puissance.

Fiche 5 : Quotient où figurent des puissances .

Fiche 6 : Puissance d’un nombre en écriture fractionnaire.

v Puissance d’un quotient

Fiche 7 : Ordre dans lequel il faut effectuer les opérations.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité 1°)Applications en sciences 2°) série 2

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : Puissance d’un entier ou d’un décimal positif.

Ecrivez le produit de « 9 » nombres égaux à « 7 ».

Vous remarquez que c’est long à écrire ! Heureusement qu’il n’y en a pas « 379 » (par exemple )… Pour simplifier cette écriture , on décide , par convention , de la noter :  :

Donc =

7

7

7

7

7

7

7

7

7

: se lit «  sept exposant « 9 ». « 9 » est l’exposant , il indique le nombre de facteurs .

;  ;  ; sont des puissances de « 7 » ; est la puissance de « 7 » d’exposant « 9 ». Si il y avait eu « 379 » facteurs égaux à « 7 » , on aurait écrit :

= .. ………………………………………..

Conseil : Habituez - vous à dire est le produit de 5 facteur égaux à « 2 » .

Activité :

Opérations

Décomposition

Résultat recherché

Erreur de traduction

Résultat qui a conduit à l’ erreur .

=

…………………………

= …...

2 x 8

= …64..

=

…………………………..

= …..

= …..

=

……………………………..

= …..

= …..

=

………………………………..

= …..

= …..

=

……………………………….

= …..

= …..

· Que pouvez-vous dire des 2 résultats trouvés sur chaque ligne ?...................

Etc……

· « » étant un nombre non nul ,

· =

Remarque : On parle de même de puissances de décimaux : Ainsi :

A retenir : «  » étant un nombre décimal et « » un entier supérieur ou égal à « 2 » , « » facteurs égaux à «  »

Par convention , on écrit : et si ; remarque ne signifie rien..

Puissance de dix ( 10 )

Info +++@

C’est un « 1 » suivi de « … » zéros

C’est un « 1 » suivi de « …. » zéros

A retenir : «  » étant un entier supérieur ou égal à «  ». , c’est un « 1 » suivi de «  » zéros.

Remarque :

Si = 1 ,

C’est un « 1 » suivi de « ….. » zéros

Si = 0 ,

C’est un « 1 » suivi de « ……» zéros

Fiche 2 : Produit de puissances d’un même nombre.

Info +++@

Justifiez oralement ..ces égalités

· D’une manière générale , «  a » étant un décimal , « m » et « n » des entiers ( )

Cas particuliers : Si «  = 1 » ( ou = 1 ) ; Si «  = 0 » ( ou = 0 ) ; et ;

A retenir : « a » étant un décimal non nul , « m » et « n » des entiers positifs,

Remarque : cette formule peut se généraliser à plus de deux facteurs . ( Expliquez oralement) Exemple :

Activité 1 : Complétez en utilisant la formule précédente ( «  » et «  » sont des nombres positifs)

=

Activité 2 : On vous demande d’ écrire « » sous forme de produit de puissances de « 7 » et « 3 ».

=

· On vous demande d’écrire « B » sous forme de produit de puissances de « 2 » , de « 3 » , et de « 7 ».

;

· On vous demande d’écrire « B » sous forme de produit de puissances de « a »et de « b » ( « a » et « b » sont des nombres )

Activité 3 : A votre avis , est –il un nombre très grand ?

Environ combien ?

100

1 000

1 000 000

1 000 000 000

1 000 000 000 000 000

Encadrez la bonne réponse et barrez les autres . Vérifiez par le calcul (dites cela à l’oral )…..

Fiche 3 : Puissance d’un produit de décimaux positifs.

Info +++@

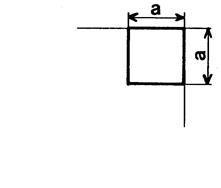
Voici ci-contre un carré dont la mesure de la longueur du côté ( en mm ) est « a ». Considérons un autre carré dont la longueur du côté est le triple de celle précédent. A votre avis , l’aire du grand carré est combien de fois plus grande que celle du petit ?..............

On vous demande de vérifier le résultat , dessinez le grand carré et comptez combien il contient de petits carrés. Combien en trouvez – vous ? ………..

· Vous allez le vérifier maintenant par le calcul . - La mesure de l’aire du petit carré ( en mm² ) est égale à : - La mesure de l’aire du grand carré ( en mm² ) est égale à : .

En définitive : L’aire du grand carré est « 9 » fois plus grande que celle du petit.

v En vous aidant du calcul fait précédemment , on vous demande de transformer :  :

D’une manière générale , « » et «  » étant des décimaux et « » un entier ( )

· Etudiez les cas où «  » est égal à « 1 » ou « 0 ».

A retenir : «  » et «  » étant des décimaux non nuls, et « » un entier positif .

Notation équivalente :

Remarque : Cette formule peut se généraliser à plus de deux facteurs . ( voir réponse orale )

Activités 1 :Transformez en appliquant la règle précédente ( les lettres désignent des nombres ) .

Complétez le calculez :

Activités 2 :En faisant apparaître une puissance de « 10 » , calculez « D » . D =

Commencez par regrouper les « 2 » puis les « 5 » . D = Mais vous venez de voir que Donc D =

Faîtes de même pour : F ; F =

Fiche 4 : Puissance d’une puissance.

Justifiez oralement ces égalités…

c’st à dire

· D’une manière générale , «  » étant un décimal , «  » et «n » des entiers ( ) ,

Chaque facteur «  » est le produit de combien de facteurs égaux à « a » ? .. ………… Au total , il y a donc combien de facteurs égaux à « a » ?............................................... En définitive = Etudiez les cas où «  » et «  » sont égaux à « 1 » ou « 0 » .

A retenir : «  » étant un décimal non nul, «  » et « » des entiers positifs .

Activités 1:

……………..

Attention !!!!!

………..

Et :

Activités 2: Ecrivez « H » sous forme de produit de puissances de « 3 » , « 5 » et « 7 » . =  : …………………………………………………………………………………….

Activités 3: Ecrivez «  R » sous forme de produit de puissances de « 2 » et de « 5 »., puis calculez « R » en faisant apparîatre des puissances de « 10 ».

;

;

Fiche 5 : Quotient où figurent des puissances .

Simplifions : ; . On peut écrire =

De même :

Remarque : Pratiquement , on ne détaille pas les produits , on écrit directement :

Faites de même pour :

· Simplifions puisque et , on peut écrire

· Simplifions de même :

v Vous savez calculer le produit de nombres en écriture fractionnaire : Calculez en simplifiant :

· Faites de même pour :

Fiche 6 : Puissance d’un nombre en écriture fractionnaire

Les règles de calculs sont les mêmes que pour les décimaux.

=

· Calculez : =

· Complétez :

v Puissance d’un quotient .

v D’une manière générale, «  » et «  » étant des décimaux non nuls et «  » un entier ,

Cas particuliers :

Si «  = 1 » ; et donc Si «  = 0 » ; et donc

A retenir : «  » et «  » étant des décimaux non nuls, et « » un entier positif .

Activités  1:

= =

Activités 2 :

Simplifiez :

Simplifiez

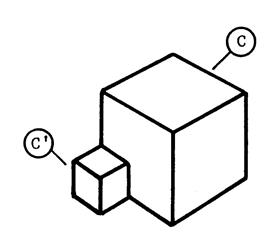
Activité 3 : Voici deux cubes « C » et « C’ » de volumes respectifs « V » et « V’ ». Désignons par «  » la longueur de l’arête du cube « C ». Et par «  » la longueur de l’arête du cube « C’ » . On sait que «  =  »

Quelle fraction de « V » représente « V’ » ? ( Trouvez une équation ( égalité ) de la forme « V’ = ….V »

Fiche 7 : Ordre dans lequel il faut effectuer les opérations.

Info ++ sur les priorités de calculs.

Répondez à la question :Comment doit-on s’y prendre pour calculez ? 1°) Calculez : « le carré du double de 5 » : Procédure  : On cherche d’abord le ………double ……….de « 5 » : on obtient  : … … Puis on calcule le ……………………… : on obtient : …………… Ce qui s’écrit : ( 2 …….. )² = …… ² = ……….

2°) Calculez : « le double du carré de 5 » : Procédure  : On cherche d’abord le ………carré ……de « 5 ». On obtient : .. ……….. Puis on calcule le .. ………….. . On obtient : .. ……………….. Ce qui s’écrit : = Trouvez- vous le même nombre dans les deux cas ? .. …

Ø représentant un nombre quelconque . «  le carré du double de  » s’écrit en mathématiques : «  le double du carré de  » s’écrit en mathématiques :

Attention : D’une manière générale , ne cofondez pas : et Dans le cas , l’exposant ne porte que sur «  ».

A retenir : En l’absence de parenthèses , quand dans un calcul , il y a des multiplications et des « puissances » , on doit effectuer d’abord le calcul des puissances. L’exposant s’applique uniquement au nombre qui le précède.

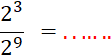
Activités 1  : Calculez .

Activités 2 : Complétez .

«  »

«  »

1

2

5

49

36

300

64

Activité 3 :

Simplifiez l’écriture des produits suivants . ( Les lettres désignent des nombres ) .

TRAVAUX AUTO FORMATIFS :

CONTROLE :

1. Dans un calcul de puissance, de quoi dépend le signe du résultat ?

2. Quel est le signe du résultat d’un « carré » ?
3. A quelle opération correspond l’écriture : 2²

EVALUATION :

Niveau 5 : (minimum)

1°) Compléter le tableau :					TC2		E	T	C
x	8	170	5,5	0,29		92
x^2

Calculer :

( - 2 ) ⁴ =

- 2 ⁴ =

Calcul mental : savoir «  par cœur » les carrés parfaits des nombres de 1 à 13 , et des dizaines et des centaines .

Remplir le tableau suivant : faire les Calculs ( voir les études de fonction )

Pour x =	-1	0	2	3	4	5	6	7
y = x^2 – 4 x + 3