DOSSIER :  Comparaison des carrés de deux nombres positifs.

Calculs

Activités « géométrique » et « carrés »….

COURS

Complétez en utilisant les signes >  ou < :

Calculs

Calculs

5 …< ..12

5 ²  =  25

12² = 144

5²  …< … 12 ²

0,6 …< … 1

0,6 ²  =  0,36

1 ² = …1 ..

0,6 ²  …< … 1 ²

0,02 … < …0,03

0,02 ² =  0,0004

0,03 ² = 0,0009

0,02 ²  … < …0,03 ²

Ces exemples vous suggèrent l’énoncé suivant :

Si des nombres positifs sont rangés dans un certain ordre , alors leurs carrés sont rangés dans cet ordre.

Est-on certain que cet énoncé est toujours vrai ? ……………………

Pour pouvoir l’affirmer, il faudrait vérifier tous les cas  ( ce qui est impossible ) ou alors faire un raisonnement en utilisant des lettres représentant  tous les cas.

C’est ce que nous allons faire….

Activités « géométriques » et « carrés »….

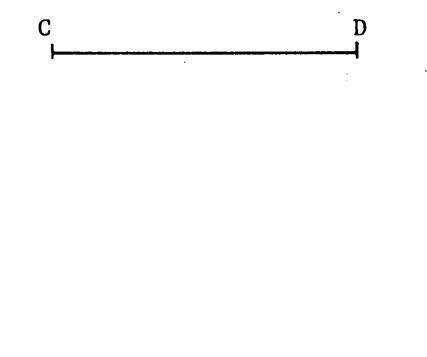
Nous désignons  par « a » et par « b » , deux nombres positifs quelconques tels que «  a < b » étant positifs , ils peuvent être considérés comme les mesures ( avec une certaine unité) de la longueur de deux segments.

Imaginons que « b » soit la mesure de la longueur du segment [ CD ]  ci-contre .

·       Placez un point « M » sur  [ CD  tel que « a » soit la mesure de la longueur du segment [ CM ]  .

Puisque «  a < b » alors « M »  situé  entre « C » et « D ».

Construisez le carré « CDEF » et le carré « CMNP » tel que « P » soit situé  sur [ CF ] 

·       La mesure de l’aire du carré « CMNP » est  « a² » la mesure de l’aire du carré « CDEF » est …….( avec la même unité)

Puisque le carré « CMNP » est à l’intérieur du carré « CDEF », alors l’aire de « CMNP » est plus petite que l’aire de « CDEF ». Donc   « a² ….b² ».

On peut donc dire :

« a » et « b » étant des nombres positifs quelconques , si « a < b »  alors …..   « a² < b² » .

Inversement :

« a » et « b » étant deux nombres positifs, si  « a² < b² » peut-on affirmer que « a < b » ?

Sachant que « a² < b² »  , trois possibilités pour « a » et « b » sont envisageables :

-        « a = b » : c’est impossible car on aurait  «  a² ..= ..b² »

-        « a > b » : c’est impossible car on aurait  «  a² …b² »  ( d’après ce qui précède )

-        «  a < b » : c’est le seul cas possible. On dira  alors :

« a »  et « b » étant des nombres positifs quelconques , si « a² < b² » alors ……..

A retenir :

Les nombres positifs sont rangés dans le même ordre que leurs carrés.

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°) que désigne "n" dans un nombre décimal ?

I) Donner la signification des relations mathématiques suivantes:

n    <   x    <  n+1  :..............................................................................................................

n²    <   x ²  <  (n+1)² :

……………………  ............................................................................:

n³    <   x ³  <  (n+1)³  :.......................................................................................................

II) Donner la signification de la relation mathématique:

                          nⁿ    <   x ⁿ   <  (n+1)ⁿ

EVALUATION:

 I)   Encadrement de  Xⁿ par  deux nombres entiers consécutifs.

a ) Pour  les valeurs de x suivants :  (compléter le tableau )

II) donner l’encadrement de  X² par  deux nombres par  deux carrés consécutifs

 (compléter le tableau )

III) donner l’encadrement de  X³ par    deux cubes consécutifs; (compléter le tableau )