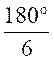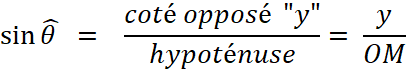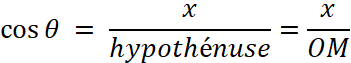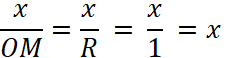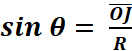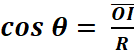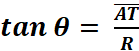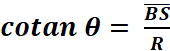Pré
requis: ce qu’il aurait fallu voir !
|
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
Objectif
suivant : |
|
|
|
|
|
|
|
DOSSIER :
le
cercle trigonométrique
|
|
|
|
|||||||
|
|
PARTIE 1
: |
|
|||||||
|
|
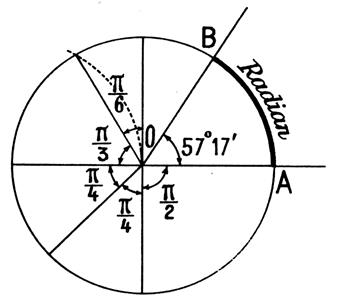
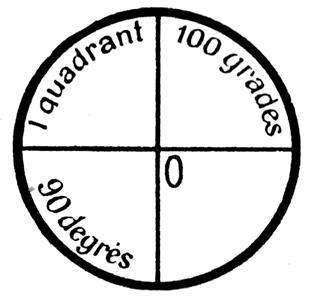
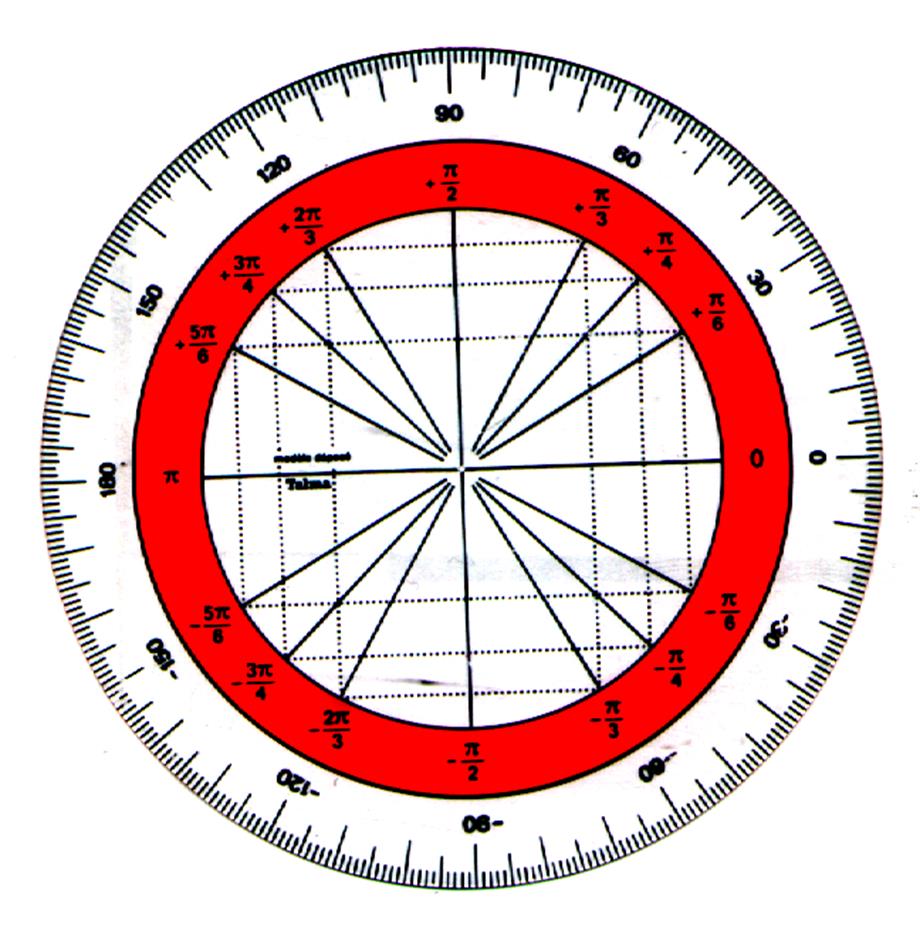
1°) Rappel : la valeur angulaire d’un arc de
cercle peut s’exprimer en degré , grade ou radian. |
|
|||||||
|
|
|
|
|||||||
|
|
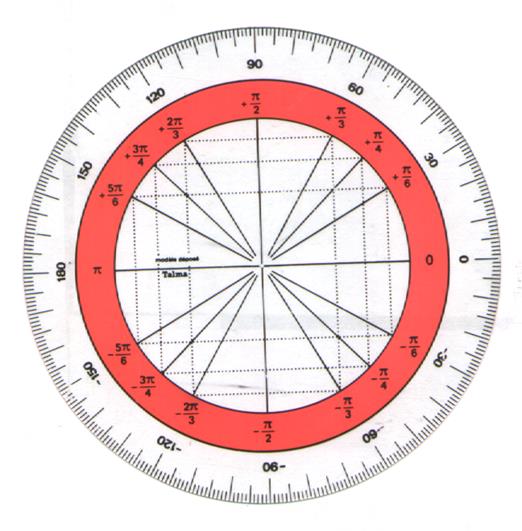
2°) GRADUATION du cercle
trigonométrique :
|
|
|||||||
|
|
|
|
|||||||
|
|
3°)
Valeurs caractéristiques du
cercle trigonométrique . |
|
|||||||
|
|
|
|
|||||||
|
|
PARTIE 2 : |
|
|||||||
|
|
1°) LE
CERCLE « trigonométrique » : SENS « positif ». |
|
|||||||
|
|
|
|
|||||||
|
|
2°) CERCLE
TRIGONOMETRIQUE : définition |
|
|||||||
|
|
|
|
|||||||
|
|
3° ) Découverte des relations
trigonométriques dans le premier
cadran du cercle . |
|
|||||||
|
|
|
|
|||||||
|
|
4°) Axe des sinus
: |
|
|||||||
|
|
|
|
|||||||
|
|
5°) Axe des cosinus
: |
|
|||||||
|
|
|
|
|||||||
|
|
6°) En résumé : caractéristiques du cercle
trigonométrique |
|
|||||||
|
|
|
|
|||||||
|
|
7°) Conventions : Désignations des axes de
coordonnées : ( sinus ;cosinus ;tangente ;cotangente) |
|
|||||||
|
|
|
|
|||||||
|
|
8°)
Tangente et cotangente : |
|
|||||||
|
|
|
|
|||||||
|
|
9°) Remarque……. |
|
|||||||
|
|
|
|
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
TEST |
Interdisciplinarité :
|
|
|||||||
|
|
COURS
|
|
|
PARTIE 1
: |
|
|
|
|
|
1°)
Rappel : la valeur angulaire d’un arc de cercle peut s’exprimer en degré
, grade ou radian. |
|
|
Les radians sont souvent utilisés pour exprimer une vitesse de rotation. Ainsi un point d’un disque qui fait un tour en 1 seconde
, on dit qu’il tourne à la vitesse
de 2 p radians
par seconde . |
|
|
|
|
|
Placez
le |
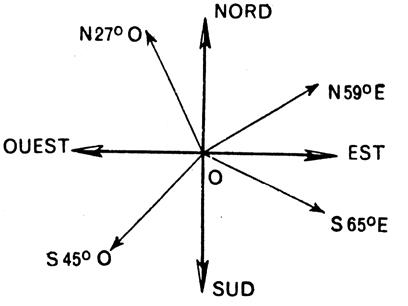
Application :
l’orientation (voir la boussole)
|
|
|
|
|
|
|
|
|
|
|
Ci-dessous
vous remarquerez les graduations
exprimées en degrés et les
correspondants en radians . |
|
|
Exemple
de graduations du cercle « en
degré » et « en radian »
|
|
|
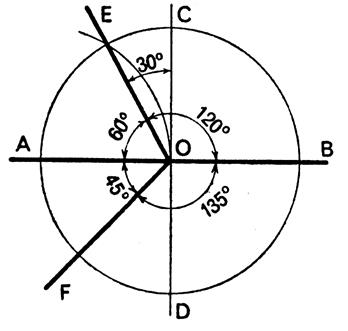
3°) Valeurs caractéristiques du
cercle trigonométrique : |
|
|
|
|
|
|
Pour un arc en :
Degrés |
Correspond en
Grade |
Correspond en
Radian |
Pour une Rotation de: |
|
360° |
400
grades |
2p |
1
tour |
|
180° |
200
grades |
p |
½
tour |
|
90° |
100
grades |
|
¼
tour |
|
45° |
50
grades |
|
1/8
tour |
|
30° = |
|
|
1/12
tour |
|
60° |
|
|
|
|
120° = 90° + 30° |
100+ |
|
¼ tour + 1/12 tour = 1/3 tour |
|
|
|
|
|
|
Et plus encore !!!!!! |
Ces informations sont utilisées en
cinématique et en dynamique. |
|
|
|
|
|
|
|
|
135° |
|
|
|
|
150° |
|
|
|
|
180° |
|
p |
|
|
210° |
|
- |
|
|
225° |
|
- |
|
|
240° |
|
- |
|
|
270° |
|
- |
|
|
300° |
|
|
|
|
315° |
|
- |
|
|
330° |
|
- |
|
|
|
PARTIE 2
: |
|
|
|
1°) LE CERCLE « trigonométrique » |
|
|
|
|
|
|
|
|
|
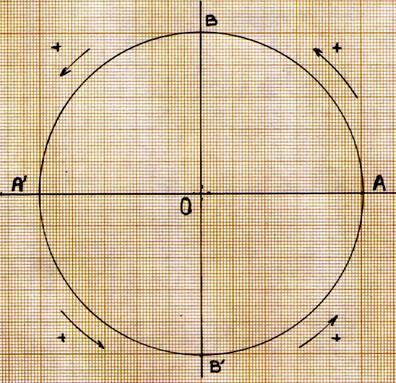
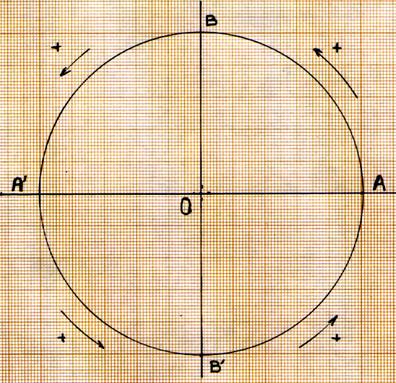
Par convention : SENS « positif » : |
|
|
|
|
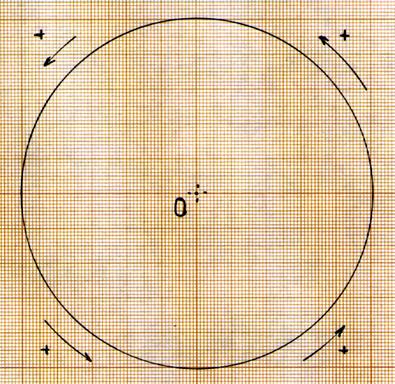
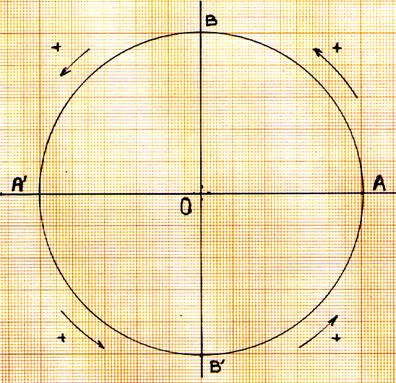
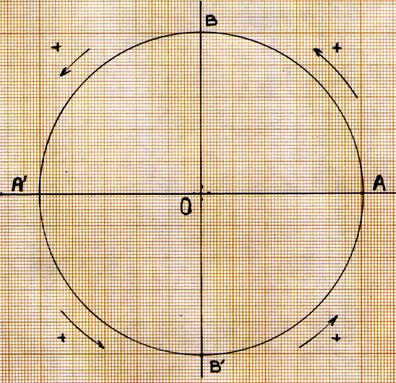
Considérons un point se déplaçant sur la circonférence du
cercle : par convention on dira que le point se déplace dans le sens
positif « + » si son déplacement s’effectue dans le sens inverse du
sens des aiguilles du montre . Ou
dans le sens inverse de la rotation de la terre. |
|
|
|
|
Par convention on a
déterminé qu’il y aurait un sens de rotation positif ou négatif. |
|
|
|
|
|
|
|
|
|
CERCLE TRIGONOMETRIQUE : définition |
|
|
|
|
Soit un repère orthonormé Le point fixe A est choisi pour origine des arcs et le rayon OA pour origine des
angles au centre . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3° ) Découverte
des relations trigonométriques dans le
premier cadran du cercle . |
|
|
|
|
|
|
|
|
|
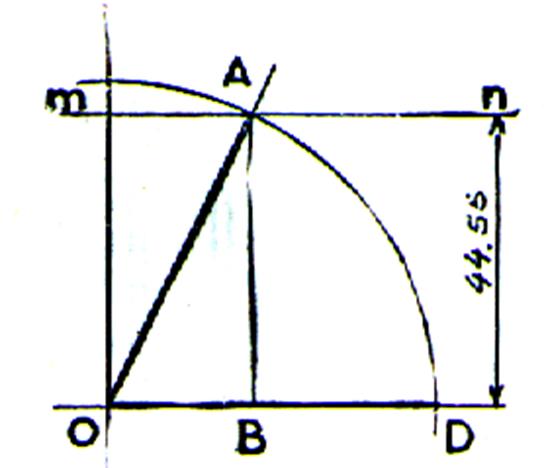
Activité
1 : recherche de la valeur numérique
du sinus ou cosinus d’un angle |
|
|
|
|
Tracez un triangle rectangle : Dont l’hypoténuse
OA mesure 100 mm : On considère l’angle « Mesurer AB : = Mesurer OB : = Diviser AB par 100 = Diviser OB par 100 = |
|
|
|
|
On dit que ( la valeur numérique du cosinus doit
être un nombre décimal avec trois chiffres après la virgule ) On dit que
( la valeur numérique du sinus doit être un nombre décimal avec trois
chiffres après la virgule ) |
|
|
|
|
Activité
2 |
|
|
|
|
« Lecture dans
la table de trigo.» : recherche de la valeur en degré d’un angle à partir de la valeur
numérique du sinus ou cosinus : |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
voir après du calcul de ensuite : complétez la phrase suivante : le nombre |
|
|
|
|
voir à quel angle correspond la valeur du
sinus « complétez la phrase suivante : le nombre |
|
|
|
|
Pour étudier la suite , il faut vous concentrer |
|
|
|
|
|
|
|
|
|
|
|
. . |
|
|
4°) Axe des sinus
: |
|
||||
|
y M On appelle « q »
l’angle AOM :
Et Conclusion,
on appelle : l’axe
« BOB’ » l’axe des « sinus » . |
|
|
5°) Axe des cosinus : |
|
||||
|
x M On appelle « q »
l’angle AOM :
conclusion :
on appelle A’OA l’axe des cosinus. |
|
|
|
6°) En résumé : caractéristiques du cercle
trigonométrique |
|
|
|
|
|
1°)
sur un cercle de centre (O) choisissons : - un point fixe A pour origine
des arcs , et
le rayon OA pour origine des angles au centre
. -
nous choisissons un sens positif de rotation qui sera le sens inverse des aiguilles
d’une montre. -
Une unité d’arc ( ou
d’angle) en degré ou grade . -
Se rappeler que
p désigne l’angle plat. -
Tout point M du cercle sera déterminé par la
valeur de l’arc AM Et tout rayon par l’angle AOM = q qui
s’appelle « angle polaire »
de M. |
|
|
|
7°) Conventions : Désignations des axes de
coordonnées : |
|
|
|
|
|
|
|
|
|
- AXE des COSINUS : Le diamètre du cercle passant par O et
aboutissant à A , avec le sens positif de O vers A ,
s’appellera « axe des cosinus ». - AXE des SINUS : Le diamètre
du cercle passant par O et aboutissant à B ,
en direction et en sens ,obtenu en faisant tourner l’axe précédent de + Sur chacun de ces axes ,
l’origine est le centre « O » , et l’unité de longueur est
obligatoirement le rayon du cercle . - AXE des TANGENTES : La tangente au cercle au point A sera orientée
comme l’axe des sinus avec origine la point A. - AXE des
COTANGENTES : La tangente au point B sera orientée comme l’axe
des cosinus , avec « B » comme origine. Sur ces deux axes ‘aussi’ , l’unité de longueur sera le rayon. |
|
|
|
|
|
|
|
|
|
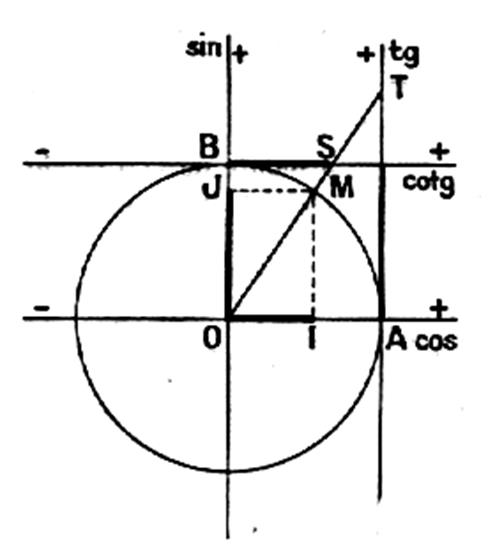
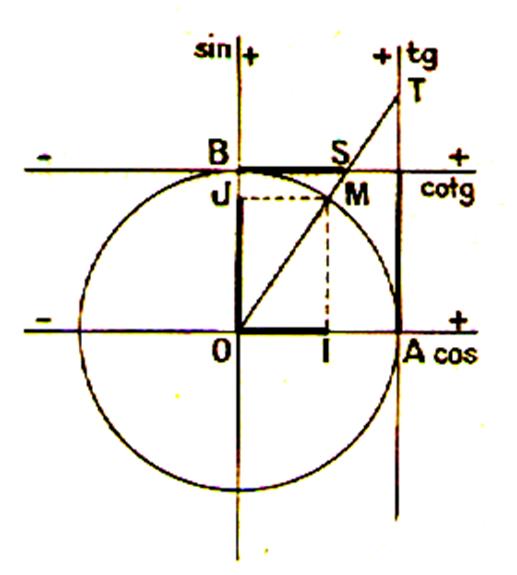
Cosinus et sinus d’un angle : Soit M un point du cercle défini par l’angle AOM = q Le rayon se projette sur les deux axes de
coordonnées en « I » et « J » ,
on appelle : « Cos
q » le nombre mesurant l’abscisse
« « sin
q » le nombre mesurant l’ordonnée « |
|
|
|
|
|
|
|
|
|
8°)
Tangente et cotangente : |
|
|
|
|
|
|
|
|
|
Les prolongements de OM coupent l’axe des
tangentes et des cotangentes en
« T » et en « S » ; On appelle Tangente d’un angle téta :
« tan
q » le nombre mesurant le segment « (
activité : tracez le segment AT ) Cotangente d’un angle téta : « cotan q » le nombre mesurant le segment « (
activité : tracez le segment BS ) |
|
|
|
|
|
|
|
|
|
Remarques : |
|
|
|
|
|
|
|
|
|
Si l’on mesure le rayon R ,
et les segments OI ; OJ ; AT et BS avec la même unité
« étrangère » à la figure ,
par exemple en millimètres, les quatre nombres trigonométriques de l’angle q sont des
rapports algébriques : |
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS.
Tracer un cercle trigonométrique , placer l’axe des sinus et des cosinus .
EVALUATION
1°) Tracer un cercle trigonométrique , placer un
point M dans le premier quadrant . tracer les mesure algébriques du sinus , cosinus , tangente, cotangente.
2°) Tracer un cercle trigonométrique , placer un
point N dans le deuxième quadrant .
Tracer les mesure algébriques du sinus , cosinus ,
tangente, cotangente.
3°) Tracer un cercle trigonométrique et placer
dessus les valeurs suivantes
|
Degrés |
Grade |
Radian |
|
|
360° |
400 grades |
2p |
1 tour |
|
180° |
200 grades |
p |
½ tour |
|
90° |
100 grades |
|
¼ tour |
|
45° |
50 grades |
|
1/8 tour |
|
30° = |
|
|
1/12 tour |
|
60° |
|
|
|
|
120° = 90° + 30° |
100+ |
|
¼ tour + 1/12 tour = 1/3 tour |
|
135° |
|
|
|
|
150° |
|
|
|
|
180° |
|
p |
|
|
210° |
|
- |
|
|
225° |
|
- |
|
|
240° |
|
- |
|
|
270° |
|
- |
|
|
300° |
|
|
|
|
315° |
|
- |
|
|
330° |
|
- |
|
Corrigé
|
|
|