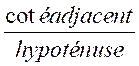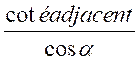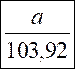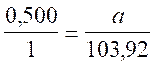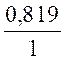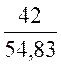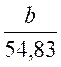|
|
Géométrie : DOSSIER : TRIGONOMETRIE /
Objectif cours 28 |
Pré requis :
|
Le système sexagésimal |
|
|
Le triangle rectangle |
|
|
Le produit en croix |
Environnement du dossier :
|
Objectif précédent : 2°) Voir les fiches travail sur
« le cosinus » en 4ème . |
Objectif suivant : |
info Présentation : liste des cours disponible sur la
trigonométrie |
|
|
|
|
|
|
DOSSIER « la trigonométrie » : COSINUS d’un angle
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé évaluation |
Les relations trigonométriques dans le triangle rectangle que nous étudierons sont au nombre de quatre. : le sinus ; le cosinus ; la tangente et la
cotangente.
|
A ) Construction et mesure d’un angle : |
|
|
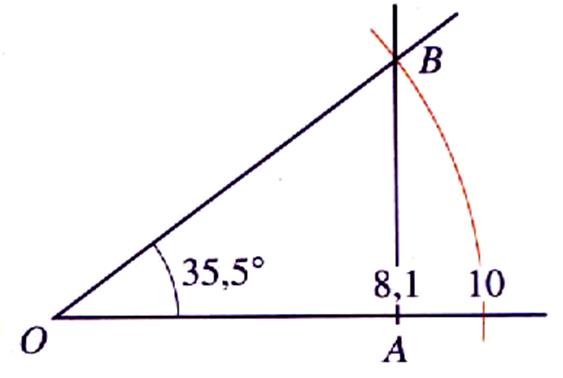
Construction :d’un
angle de 35,5°à l’aide du cosinus : |
|
|
On recherche le cosinus
de 35,5° : » 0,81 soit =
procédure de tracé : -tracer un arc de rayon 10 cm ; sur [ 0x)
placer le point « A » tel que OA = 8,1 cm tracer une perpendiculaire à [ 0x) passant par « A » et coupant l’arc de
cercle en « B » l’angle AOB vaut 35,5° (à
vérifier avec un rapporteur) |
|
|
Conclusion :pour construire un angle on peut
utiliser un rapport trigonométrique. |
|
|
B ) MESURE d’ un ANGLE : |
|
|
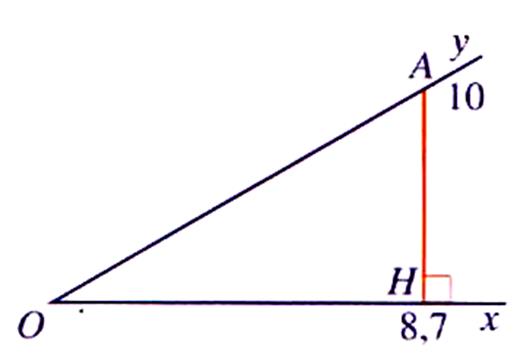
Mesure d’un angle « xOy »
donné sans le rapporteur . |
|
|
Procédure : -placer un point « A » sur [Oy) tel que OA = 10 cm ; tracer la projection
orthogonale de « A » sur
[Ox)
(image de « A » est « H ») mesurer la longueur « OH » ( = 8,7 cm) on en déduit le cosinus de l’angle « xOy » = A l’aide de la calculatrice ou
de la table : on obtient la valeur de l’angle = 29,5° |
|
COURS
|
|
I) Relation trigonométrique dans le triangle
rectangle : Le
COSINUS d’un angle . |
|
|
|
|
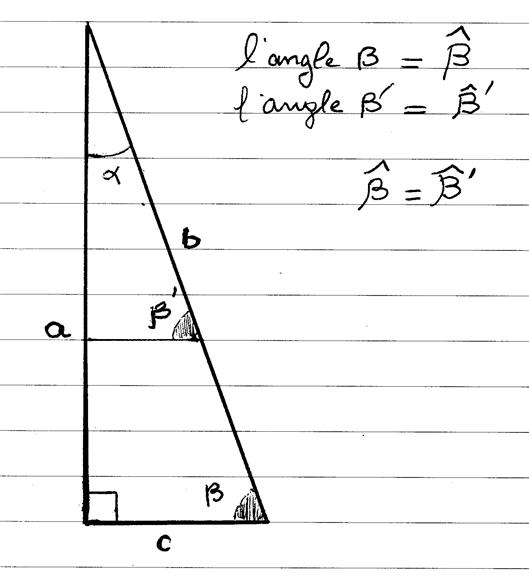
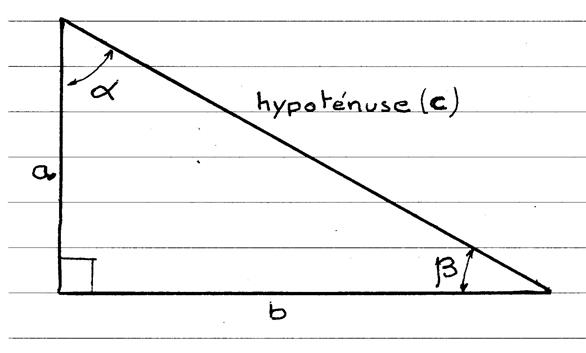
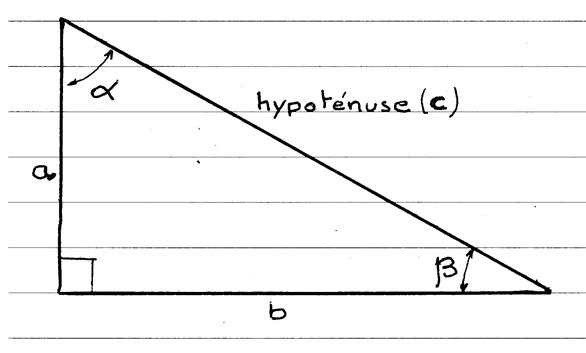
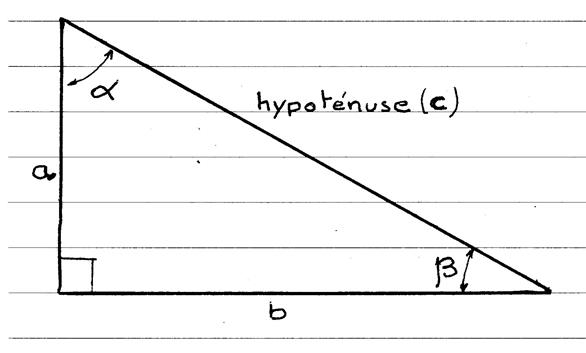
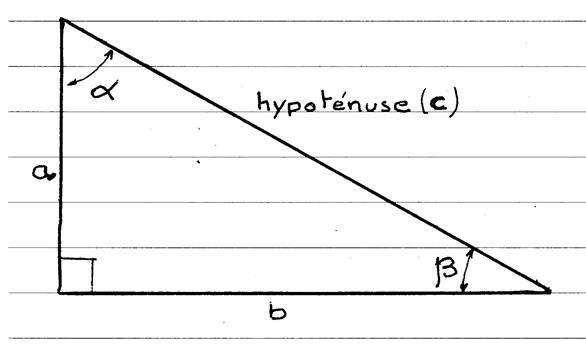
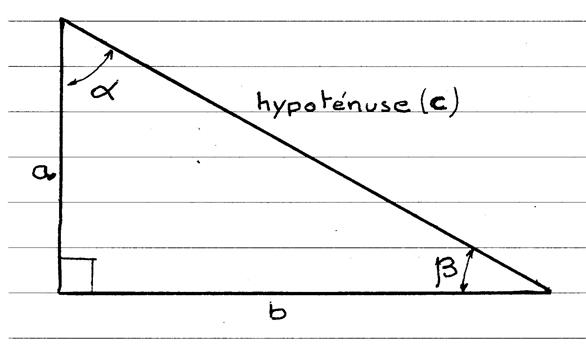
L’angle b = l ’angle b’ · Le symbole « cosinus » est
noté « cos » : · Les lettres « a » ; « b » , « c »
sont les longueurs des cotés du triangle
rectangle ; · Le coté « c » est le coté opp à l’angle a · Le coté
« a » est le coté opp. à l’angle b · « b » est l’hypoténuse du triangle |
|
|
|
|
Rappel sur les angles : (nous travailler
avec des angles exprimés en degré ) · l ‘ angle « alpha » a
pour symbole : · l ’
angle « bêta » a
pour symbole : · L’écriture « cos a » ou « cos. · L’écriture « cos b » ou « cos. |
|
|
![]()
|
|
Par définition : |
|
|
|
Le
cosinus d’un angle ; dans un
triangle rectangle ; est égal
au rapport de la longueur du coté adjacent à l’angle sur la longueur de
l’hypoténuse. Traduction : cos = Si le côté adjacent et l’hypoténuse sont les longueurs
(mesurables ; ou données ) alors la valeur numérique du
cosinus est un rationnel . ( « arrondi
à tant prés » il est un nombre décimal) qui n’a
pas d’unité. Remarque : Dans la majorité des problèmes traités au collège , la valeur du cosinus est obtenue en faisant une
« division ». On vous demande d’exprimer cette valeur et de l’« arrondir à tant prés » . Cette valeur décimale est
ensuite convertie en
« degré d’angle » soit à
l’aide d ’une table dite « de
trigo. »,soit à l’aide d’une calculatrice qui est en mémoire cette table De cette façon on peut convertir un nombre
en « degrés » , ou inversement , de degrés en nombres |
|
|
|
Remarque : Dans le cas du
cercle trigonométrique la valeur du cosinus est alors un « réel »
. (
voir un irrationnel ) |
|
|
|
|
|
|
|
II ) CONVERSION
D ‘ UN COSINUS en valeur d’ ANGLE ; et inversement : |
|
|
|
Il existe deux possibilités pour avoir la valeur d’un angle à partir
de son cosinus et inversement avoir la valeur d’un cosinus à partir de la
valeur d’un angle. avec une table numérique appelée « table de trigonométrie » avec la calculatrice
UTILISATION de la CALCULATRICE : Mise en marche de la calculatrice AC Mettre en
MODE 4 (mode
DEGré) Passage de la valeur de l’angle
exprimée en « degré » en une
valeur décimale appelée « sinus » : Afficher le
nombre de degrés :
exemple 5 2 Taper sur la touche cos Lire sur l ’écran :
valeur du cosinus : 0 , 6 156 614 75 Si l’on tape sur : INV
cos alors s’affiche le Nbre
degrés Lire sur l’écran : 52 Convertir la valeur du cosinus
en degrés (toujours dans le même mode) Afficher la valeur du cosinus : exemple : 0,540 Taper
successivement sur les
touches : INV cos Lire à l’écran : 57,31636115 Interpréter : 57° ,31.... ( le
« 31 » correspond a un le résultat est exprimé en valeur décimale Résultat par encadrement : cosinus 57°
< 0,540 <
cosinus 58° Remarque : Suivant les types de calculatrice vous pouvez
passer d’une expression de la valeur
d’un angle en écriture
« décimale » en une expression
de la valeur de l’angle en écriture « sexagésimale » . Ce qui signifie que l’on peut « rentrer » la valeur de l’angle en l’exprimant dans le système sexagésimal 20° 30’
; ou en utilisant le système décimal :
20, 5 Lorsque l’on
annonce que l’on veut avoir la
conversion en système sexagésimal , on
veut exprimer la valeur de l’angle en (Degré ,minute , seconde), Si cela est : Taper les
touches : INV ° ‘ ‘’ Affichage à l’écran : degré ° minute’ seconde ‘’ exemple : 32 °
25 ‘ 34’’ ( lire : trente deux degré , vingt cinq
minutes et trente deux secondes ) (les
affichages sont différents suivant les
calculatrices , les affichages sont « vrais » suivant les
performances d’affichage de la calculatrice ). Taper : sur la touche ° ‘ ‘’ pour revenir à une
expression du degré en valeur décimale Exercices : Nous travaillons toujours en mode « degré »
,avec la calculatrice. 1
Cas : Quand on connaît la valeur
d’un angle ; je peux connaître son cosinus : on
connaît la valeur de l’angle ( en degré ) : le cosinus est un
nombre que l’on obtient en consultant la table numérique sur les cosinus des angles. Exemple : le cosinus de 53° se
note cos 53° ; d’après la table
numérique (ou avec l’aide de la calculatrice ) je
trouve : 0,602 (valeur
arrondie) en résumé on écrira : cos 53° = 0,602 exemples : cos 54° = 0,588
cos 35° 20’ = cos 35°,33 = 0.816
cos 72° 13’ » 72° 10’ = 72°,17 = 0,306 2 Cas : Quand
on connaît le cosinus d’un angle ,on peut connaître
l ’ angle concerné par cette valeur on donne le cosinus de l’angle ; alpha vaut
0,8 ;( ce qui se traduit par
l’écriture : cos a = 0,8 ) trouver
la valeur de l’angle alpha (la valeur de l’angle sera obtenue en consultant la table de « trigo » sur les cosinus ;(ou
alors j’utiliserai la calculatrice). Réponse : si
cos a = 0,8
alors ;d’après la table numérique a = 36,87° Autres exemples : cos a =
0,857 ; a = 31° cos x =
0,433 ; x =
64,°34 cos a
= 0,511 ;
a =59°,27 Que ce soit avec la table numérique ou la
calculatrice nous obtenons toujours le même résultat. Remarque :à ce
niveau d’exercices il n’y a pas de calcul , nous ne faisons que de la lecture
de table numérique. |
|
|
|
Soit un triangle rectangle : |
|
||
|
|
|
|
|
|
|
|
Traduction
mathématique : cos
a = Attention : le coté opposé
et l’hypoténuse sont des grandeurs qui
doivent avoir la même unité
. (ce sont des
longueurs exprimées soit en mm ;en cm , .....) Si on
applique cette égalité au triangle rectangle ,dessiné ci-dessus : cos b = cos
a = Dans le
triangle rectangle : la longueur de l’hypoténuse est toujours supérieur
à la longueur du coté
adjacent ; donc dans le rapport « coté adjacent sur
hypoténuse » ,le nombre
est toujours supérieur à 0
et inférieur à 1. Traduction : 0 Le modèle mathématique
( l’outil ) du calcul du cosinus d’un angle est une
division (voir la même chose pour le sinus ) : exemple : soit 3 = si 3
= donc on peut
en déduire que 6 = 3 ou
on peut aussi en déduire que
2 = ainsi à
partir de cet exemple (qui est vrai)
on peut écrire que si : cos a = alors par
transformation coté adjacent =
cos a et que ,toujours ,par
transformation : hypoténuse = Il est toujours possible ,si on connaît deux
valeurs numériques sur trois ,on peut retrouver la valeur de la troisième par
calcul . |
|
||
|
|
APPLICATIONS : Soit un triangle rectangle : |
|
||
|
|
|
|
|
|
|
|
EXERCICE RESOLU
N° 1 Calcul
d’un coté
dans un triangle rectangle : On donne : l’hypoténuse égale
à :..103.92 mm........
l’angle a =
...60°.......................... Calculer : la longueur de « a » Correction : 1°)
On sait que : cos a = on sait que la valeur decos 60° = 0.5
;Hypoténuse = 103,92mmm ;coté adj = a 2°) on remplace dans (1) 0 ,500
= 3°) Calcul : 0 ,500 = transforme : On fait le produit en croix :
0,500 51,96 = a
Résultat : au mm prés a
= 52 mm EXERCICE RESOLU N° 2
Calcul d’un coté dans un triangle rectangle : On donne : longueur du coté
adjacent à b = 100 mm ........ l’angle b = ...35° Calculer : la longueur de L’hypoténuse Corrigé : cos b = Calcul :
0,819 x = 100
donc x =
100 : 0,819 x= 122,1
Résultat :
l’hypoténuse à pour longueur : 122 mm |
|
|
|
EXERCICE RESOLU N° 3 Calcul
d’un angle dans un triangle
rectangle : Soit un triangle rectangle : |
|
|
|
|
|
|
|
|
|
On donne : l’hypoténuse égale à :.54,83 mm........
le coté a = 42 mm Calculer : l’angle : a Corrigé : d’après la relation cos a = donc on remplace les mots par leur
valeur : cos a
= on fait la division : cos a
= 0,766 004012 On cherche la valeur de l’angle :
d’après la calculatrice a = 40° Conclusion a
= 40° Remarque :si dans un triangle
rectangle je connais deux angles , j’en déduis le troisième ( somme des angles = 180° , somme des angles complémentaires =90° );si je
connais aussi la longueur (ou mesure)
d’un coté , je peux ,en utilisant la relation sur
le sinus trouver la valeur d ‘un
deuxième coté , puis du troisième. Suite de l’exercice N ° 3 L’angle a = 40°
; j’en déduis que
l’angle b = 90 -40 =
50° ensuite j’applique la relation : cos b = soit cos50°
= Donc « b» = 35,26 mm (refaire la figure à l’échelle 1 et vérifié) Récapitulatif de l’exercice N°3 : Dans un triangle rectangle ;
connaissant deux mesures (La longueur
de l’hypoténuse et la longueur d’un coté du triangle),j’ai pu retrouver la valeur des deux
angles complémentaires ainsi que la
longueur du troisième coté du triangle : Avec : (deux mesures) l’hypoténuse égale à :.54,83 mm. ; le coté a = 42 mm j’ai calculer la valeur
permettant d’obtenir l’angle a = 40° ; puis de
l’angle b = 90 -40 = 5° ce
qui m’a permis de calculer la valeur de
« b » = 35,26 mm |
|
|
|
TRAVAIL à
faire : Soit un triangle rectangle : |
|
|
|
|
|
|
|
I ) Compléter
le tableau : ( prendre a = 60° )
|
hypoténuse |
12 |
|
|
|
|
a |
|
33 |
|
0,866 |
|
b |
|
|
1 ,25 |
|
|
cos 60° |
|
|
|
|
II ) Compléter le
tableau suivant :
l’angle a = 60°
|
hypoténuse |
12 dm |
|
|
|
|
a |
|
33 cm |
|
0,866 m |
|
b |
|
|
1 ,25 dm |
|
|
Cos 60° |
|
|
|
|
III) Compléter le tableau :
|
hypoténuse |
12 dm |
|
|
1 m |
|
a |
|
33 cm |
|
0,866 m |
|
b |
|
|
1 ,25 dm |
|
|
cos b |
|
|
|
|
|
cos a |
|
|
|
|
|
b |
|
|
|
|
|
a = |
60° |
30° |
45° |
|
|
|
TRAVAUX AUTO FORMATIFS : CONTROLE : 1°) Traduire en langage littéral : « cos
a » lire : « cos b » lire : 2°) Traduire en symbole mathématique : « cosinus
de l’angle alpha » :
………………………………….. « cosinus de l’angle bêta » :
…………………………… 3°) Traduire en langage
littéral : cos a = 4°) Traduire en langage mathématique « Le
cosinus d’un angle ; dans un triangle rectangle ; est égal au rapport de la longueur du
coté adjacent sur la longueur de l’hypoténuse. » 5°) Compléter les phrases suivantes
: · Le cosinus est un nombre qui n’a pas ................. ;Précisez ses limites
numériques en fonction des angles ......... · Quand on connaît le cosinus d’un angle
........................................... · Quand on connaît la valeur d’un
angle ......................................... 6°)
*Donnez la définition littérale d’un « cosinus ». 7°) Donnez son modèle mathématique. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
EVALUATION : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Compléter
les tableaux suivants : Avec la table :
Avec la calculatrice :
Au choix
(calculatrice ou table)
Soit
un triangle rectangle : (Voir la figure
ci-dessus ) I ) Compléter le tableau :
( prendre a = 60° )
II ) Compléter le
tableau suivant : l’angle a = 60°
III) Compléter le tableau :
Au choix
(calculatrice ou table)
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
xd |
Soit un triangle rectangle : |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
I ) Compléter le tableau :
( prendre a = 60° )
II ) Compléter le
tableau suivant : l’angle a = 60°
III) Compléter le tableau :
|
|