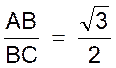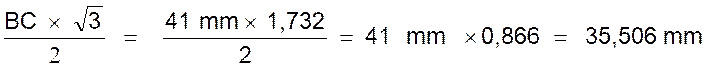Index   warmaths

Objectif précédent :

Les pré requis  à l’étude de la trigonométrie .  

Objectif suivant

1°) Présentation

2°) activités  préparatoire

Liste des cours sur la trigonométrie    

INFO:      Les NOTIONS élémentaires de TRIGONOMETRIE

LECTURE : Passage de la résolution graphique (La géométrie )  à la résolution numérique des triangles.( La trigonométrie)

Résolution graphique d’un triangle et ses limites .

La géométrie permet de construire un triangle connaissant trois de ses éléments dont au moins un côté. La construction terminée, il est possible de mesurer les trois autres éléments avec les instruments de mesure utilisés en dessin , double décimètre pour les côtés et rapporteur pour les angles.

Cette résolution graphique du triangle présente les inconvénients suivants :

a)    la construction et la mesure des éléments donne des résultats peu précis à cause des imperfections des instruments utilisés ou de l’insuffisance de l’œil du dessinateur ( il est difficile de mesurer des de millimètres et d’évaluer les angles avec une approximation supérieure au demi- degré )

b)    Les erreurs minimes commises dans le tracé des angles se traduisent par des erreurs souvent très grandes sur la longueur des côtés ; l’emploi des échelles de réduction utilisées en dessin amplifient encore ces erreurs dans les résultats des mesures définitives ;

c)     Une construction soignée entraîne toujours des pertes de temps.

En géométrie ordinaire , on trouve des relations précises (des égalités) entre les angles d’une même  figure , par exemple d’un triangle :  = p ; ou entre les segments d’une même figure , par exemple le théorème de Thalès ; mais jamais  de relation précise où figurent à la fois les angles et les segments : de telle sorte que , sauf dans des cas très rares , il est impossible , connaissant les uns , de calculer les autres .

Par ailleurs , en géométrie nous pouvons déterminer la longueur des lignes « inaccessibles » par la construction de triangles semblables,c'est-à-dire par l’emploi du rapporteur et de l’échelle de proportion ; mais on doit reconnaître bientôt que ,quelques soins on peut apporter à ces constructions graphiques,l’imperfection des instruments ne donne que des solutions insuffisantes et entraîne souvent même des erreurs assez considérables.

La résolution numérique des triangles : LA TRIGONOMETRIE.

Les géomètres ont donc été amenés à chercher des méthodes plus rigoureuses,en remplaçant les constructions graphiques par le calcul. Tel est le but de la « trigonométrie »que l’on peut définir ainsi : la trigonométrie est la science qui a pour objet de déterminer,par le calcul ,les divers parties d’un triangle ,quand on a des données suffisantes. On appelle cela « résoudre un triangle »

La trigonométrie fournira des relations précises où entreront à la fois  segments et angles .

Encore les angles n’y entreront – ils – pas directement , mais par l’intermédiaire de certains nombres qui leur sont attachés.

Par exemple :

                     Si dans un triangle rectangle on connaît la longueur du côté opposé à un angle connu (soit 2 valeurs sur 6 ) on peut trouver les autres dimensions ( angles et longueurs ) de ce triangle .

But de la trigonométrie :

1°) La trigonométrie apprend à déterminer par le calcul les éléments inconnus d’un triangle, alors que la géométrie fournit surtout des solutions graphiques du même problème.

Cette détermination des angles et des côtés d’un triangle ‘par le calcul, est appelée « résolution » du triangle. 

La résolution numérique évite ces inconvénients . C’est ce que l’on va vous faire  comprendre l’exemple suivant

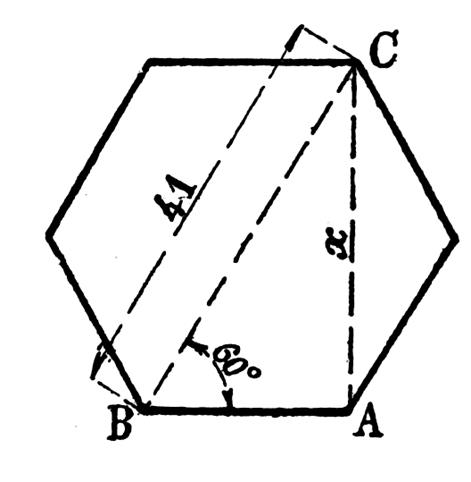
Etant donné le diamètre du cercle BC = 41 millimètres d’un profilé pour écrous à 6 pans ( hexagone) , trouver la distance « x » de deux faces opposées .

On peut anticiper le résultat à trouver :

Il est possible de trouver la valeur  approchée de « x » par le tracé , cela permet de vérifier si le calcul est cohérent et exacte.

Le triangle  ABC est rectangle , l’angle « B » = 60 ° , AC est donc la hauteur d’un triangle équilatéral dont ABC représente la moitié de ce triangle , et l’on apprend en géométrie que

donc 

AC   ou «  »  =

donc    =   35 , 506  mm

L’avantage de cette méthode apparaît immédiatement : le résultat obtenu  est donné avec précision et rapidité.

La géométrie ne permet toutefois  de l’employer que dans quelques cas particuliers correspondants aux angles de 30° , 45° ; 60 ° et 90° .

La trigonométrie généralise cette méthode et rend possible la résolution numérique pour tous les angles.