Pré requis:
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : informations sur
les triangles |
DOSSIER
:
LES
TRIANGLES :
|
|
Définitions :
|
|
|
|
Les
triangles « superposables »
|
|
|
|
Les
triangles « égaux » |
|
|
|
Les
triangles « isométriques » |
|
|
|
Les
triangles « semblables » |
|
|
|
|
|
|
Les figures sont à revoir !!! |
|
|
|
TEST |
COURS |
Interdisciplinarité
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Caractéristiques d’un
triangle : Un triangle est une figure géométrique
plane possédant 6 caractéristiques principales : n 3 angles ( de
même valeur angulaire ou pas) n 3 cotés ( de même
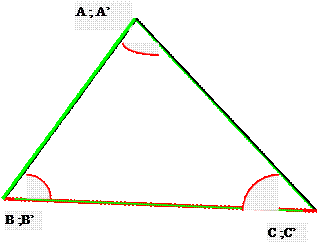
longueur ou pas ) I ) Triangles égaux : Deux
triangles sont dit « égaux » si tous leurs points sont communs. Les
figures sont superposées, cela implique qu’elles ont les mêmes mesures :angles et longueurs)
Les
triangles ABC et
A’ B’ C’ sont égaux , ils se superposent .Leurs sommets sont superposés. II ) Triangles
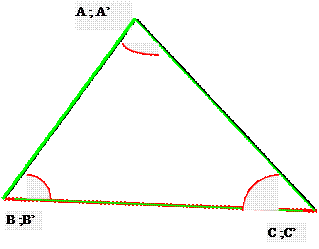
isométriques : Deux
triangles sont isométriques s’
ils ont les mêmes mesures .( longueurs et angles ). Remarques : si des triangles ne sont pas superposés mais s’ils ont les mêmes mesures (angles et longueurs) ils sont alors égaux et
isométriques.
B C Des figures géométriques sont dites « isométriques » si elles
ont les mêmes mesures le longueurs et mêmes mesures d’angle
. III ) Les triangles semblables. Pour les calculs voir :Objectif
« proportion » et fonction linéaire. Deux triangles sont semblables si : -leurs angles sont égaux deux à deux ; -les cotés opposés aux angles « égaux » sont proportionnels.
Exemple N° 1
Les côtés opposés aux angles
égaux sont appelés « côtés homologues » Les triangles ABC et A’B’C’ sont dits
« semblables » si : L’angle A
est égal à l’angle A’ ( Â = Â’ ) L’angle B
est égal à l’angle B’ ; (¨ L’angle C
est égal à l’angle C’ ; ( et si les
rapports AB / A’B’ ; BC
/B’C’ ; AC / A’C’. sont égaux : Commentaires : Pour savoir si deux triangles sont semblables ,il
existe deux méthodes : 1°) Par la mesure avec un rapporteur :vérifier si les 3 angles de l’un des
triangles sont égaux aux trois angles de l’autre triangle. 2°) Par le calcul :prendre
les mesures des longueurs et vérifier
si les rapports des cotés opposés aux angles sont proportionnels (attention
de conserver l’ordre dans le choix des cotés du premier triangle par rapport
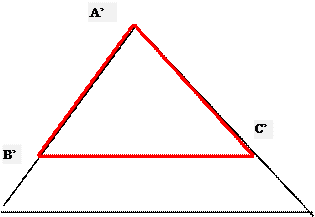
au second triangle.) Remarques : I ) Tracé de deux
triangles semblables : les
triangles semblables tracés dans un
plan peuvent occuper des positions
différentes ; (aucun coté d’un triangle à un angle de même mesure ne se trouve parallèle
en eux .( ce qui ne veut pas dire qu ‘
aucun coté d’un triangle ne se trouve parallèle à un coté d’un autre
triangle). II )En règle générale : Des triangles semblables ne seront pas
isométriques. (ils n’ont que les 3 angles de même mesure.) III ) (si un coté d’un triangle
est parallèle à un coté d’un second
triangle alors on dira que les triangles sont homothétiques) ont dit que
les TRIANGLES sont SEMBLABLES ET HOMOTHETIQUES |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Caractéristiques d’un triangle :
Un
triangle est une figure géométrique plane possédant 6 caractéristiques
principales :
n 3 angles ( de
même valeur angulaire ou pas)
n 3 cotés ( de même longueur
ou pas )
I ) Triangles égaux : Deux triangles sont dit
« égaux » si tous leurs points sont communs.
Les figures sont superposées, cela implique
qu’elles ont les mêmes mesures :angles et
longueurs)
Les triangles
ABC et A’ B’ C’
sont égaux , ils se superposent .Leurs sommets
sont superposés.
Deux triangles sont isométriques s’ ils ont les mêmes mesures
.( longueurs et angles ).
Remarques : si des
triangles ne sont pas superposés mais
s’ils ont les mêmes mesures (angles et longueurs) ils sont alors égaux et
isométriques.
|
B C |
||||||||||||||||||||||||||
Des figures
géométriques sont dites « isométriques » si elles ont les mêmes
mesures le longueurs et mêmes mesures d’angle .
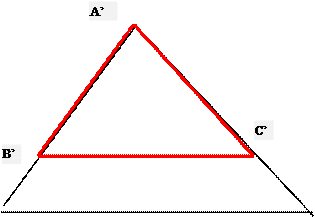
III ) Les triangles
semblables.
Pour les calculs voir :Objectif
« proportion » et fonction linéaire.
Deux triangles
sont semblables si :
-leurs angles sont
égaux deux à deux ;
-les cotés opposés aux
angles « égaux » sont
proportionnels.
|
|
Exemple N°
1
|
|
Les côtés opposés aux angles égaux sont appelés « côtés
homologues »
Les triangles ABC et A’B’C’ sont dits « semblables » si :
L’angle A est égal à l’angle A’
( Â = Â’ )
L’angle B est égal à l’angle B’ ; (¨![]() =
= ![]() )
)
L’angle C est égal à l’angle C’ ;
(![]() =
=![]() )
)
et si les rapports AB / A’B’ ; BC /B’C’ ; AC / A’C’. sont égaux :
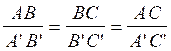 = k
= k
Commentaires :
Pour savoir si deux
triangles sont semblables ,il existe deux
méthodes :
1°) Par la mesure avec un rapporteur :vérifier si les 3 angles de l’un des
triangles sont égaux aux trois angles de l’autre triangle.
2°) Par le calcul :prendre
les mesures des longueurs et vérifier si
les rapports des cotés opposés aux angles sont proportionnels (attention de
conserver l’ordre dans le choix des cotés du premier triangle par rapport au
second triangle.)
Remarques :
I ) Tracé de deux triangles semblables : les triangles semblables
tracés dans un plan peuvent occuper des positions différentes ; (aucun coté
d’un triangle à un angle de même mesure
ne se trouve parallèle en eux .( ce qui
ne veut pas dire qu ‘ aucun coté d’un triangle ne se trouve
parallèle à un coté d’un autre triangle).
II )En règle
générale : Des triangles semblables ne seront pas isométriques. (ils n’ont que les 3 angles de même mesure.)
III ) (si un coté d’un triangle est parallèle à un
coté d’un second triangle alors on dira
que les triangles sont homothétiques) ont dit que les TRIANGLES sont SEMBLABLES
ET HOMOTHETIQUES
Travaux auto formatifs :
CONTROLE
1°) Quand dit - on que deux
triangles sont égaux ?
2° ) Quand dit - on que deux triangles sont isométriques ?
3° ) Compléter la phrase : deux
triangles sont dits semblables
si :.............................................
4° ) Dans la
représentation graphique quelle condition doit-on respecter pour qu’un triangle
soit semblable sans être homothétique ?
5°) Combien de procédures peut -
on utiliser pour vérifier si deux triangles sont semblables ? ;
nommer les ,expliquez.
6 ° ) En règle générale
peut - on dire que deux triangles semblables sont homothétiques ?
1°) Tracer un triangle quelconque (ni
rectangle ; ni isocèle) ; ensuite tracer le triangle égal au
précédent et un triangle isométrique.
2° ) Les angles d’un
triangle mesurent 43° et 54° .Construire un triangle « isométrique ».
3° ) Les angles A et
B d’un triangle ABC mesurent
43° et 54°,on donne BC = 40 mm Construire un triangle A’B’C’ semblable
.avec B’C’ = 55mm
4°) Construire
deux triangles égaux
5°) Construire deux triangles isométriques.
6°) Construire deux triangles semblables.
7°) Construire deux triangles semblables et isométriques .
CORRIGE
CONTROLE
1°) Quand dit -
on que deux triangles sont égaux ?
Deux triangles sont égaux si ils sont superposables. (commentaire : ils sont identiques)
2° ) Quand dit -
on que d’eux triangles sont isométriques ?
Deux triangles sont dit isométriques si ils ont les mêmes
mesures ( angles et longueurs) .
(commentaire :
ils sont semblables mais non superposés)
3° ) Compléter
la phrase : deux triangles sont dits
semblables si :
leurs angles sont égaux deux à deux ;
les cotés opposés aux angles « égaux » sont
proportionnels
.....
( commentaire : Ils ne sont pas superposables )
4° ) Dans la
représentation graphique quelle condition doit-on respecter pour qu’un triangle
soit semblable sans être homothétique ?
Pour que qu’un triangle soit semblable à un autre triangle sans être
homothétique il suffit de ne pas tracer les cotés opposés au même angle parallèle .
5°) Combien de procédures peut - on utiliser pour vérifier si deux triangles sont
semblables ? ; nommer les ,expliquez. : voir
page 2
6 ° ) En règle
générale peut - on dire que deux triangles semblables sont homothétiques ?
voir page 3
EVALUATION :
1°) Tracer un triangle quelconque (ni
rectangle ; ni isocèle) ; ensuite tracer le triangle égal au
précédent et un triangle isométrique.
2° ) Les angles
d’un triangle mesurent 43° et 54° .Construire un triangle
« isométrique ».
3° ) Les angles
A et B d’un triangle ABC mesurent
43° et 54°,on donne BC = 40 mm Construire un triangle A’B’C’ semblable
.avec B’C’ = 55mm
4°) soit les deux triangles suivants , dire si
ils sont : égaux
5°) soit les deux triangles suivants , dire si ils sont : isométriques.
6°) soit les deux triangles suivants , dire si ils sont : semblables.
7°) soit les deux triangles suivants , dire si ils sont : semblables et
isométriques , pourquoi ?
|
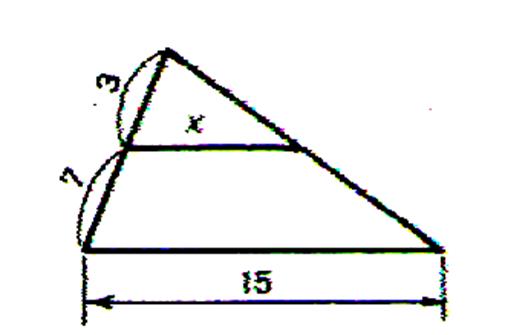
Calculer « x » |
|