COURS

A )  SEGMENTS ISOMETRIQUES :

Deux  segments  sont isométriques s’  ils ont la  même mesure de  longueurs .

Pour obtenir deux segments isométriques il faut :

Préparation : il faut tracer une droite ,placer un point A et un autre point B ,distant de A ,pour obtenir un segment ;  avec un compas on place la pointe sur A et la mine du crayon  sur  B ;

Tracé du segment isométrique : 

a) on place  un point C après B  , on place la pointe sur C et l’on trace un arc sur la droite (point F) ; le segment   CF est isométrique au segment AB

b) ou  on place la pointe sur B et l’on trace un arc coupant la droite en F (le segment BF et isométrique au segment AB ) ils ont un point commun ; l’extrémité de l’un est l’origine de l’autre .

Tracer de plusieurs segments isométriques sur une droite :

(on pourrait continuer ainsi de suite pour partager un morceau de droite en parties égales ).  

B)      ANGLES ISOMETRIQUES :

ANGLES ISOMETRIQUES :

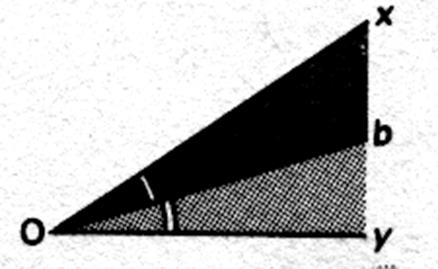
Des angles sont isométriques si ils ont la même mesure  angulaire ( mesure d’angle).

La bissectrice  d’un secteur  le partage en deux secteurs adjacents et  isométriques.

TRIANGLES ISOMETRIQUES :  (info +++)

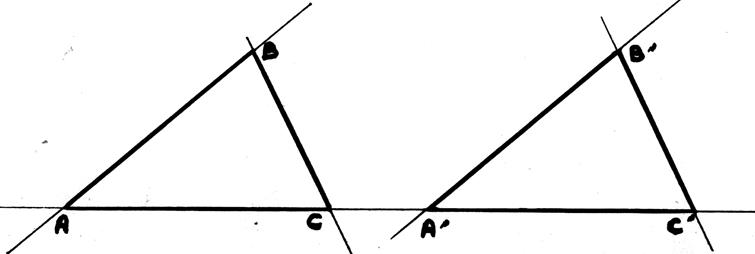
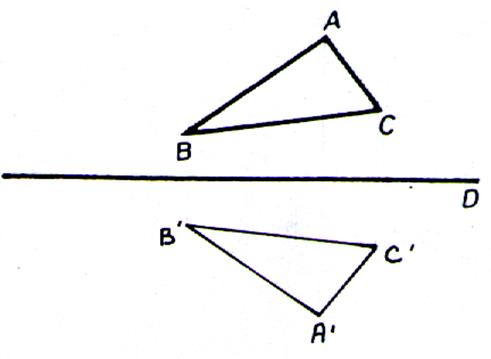
Deux  triangles sont isométriques s’  ils ont les mêmes mesures .

(  longueurs et angles )

remarques : si des triangles  ne sont pas superposés et si ils ont les mêmes mesures  ils sont alors égaux  et  isométriques.

Les triangles  ABC et   A’ B’ C’  sont des triangles isométriques.

Conclusion : Des figures géométriques sont dites « isométriques » si elles ont les mêmes mesures le longueurs et même mesure d’angle

Exemples d’activités  permettant d’obtenir par « superposition » un point ; un segment ou  une figure isométrique:

Figures obtenues par pliage ( avec un papier calque ).

POINT :

Observation et remarques :

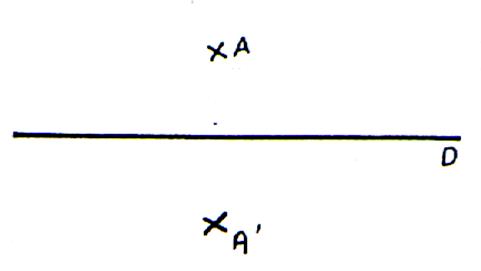
Activité :

- Placer un point  « A » sur une feuille .(plan)

faire un pli ( le nommer  D ).

- dans un demi plan P placer le point  « A » ; à l’extérieur de D.

- replier les demi-plans

- sur le demi plan P’ dessiner le point A’  (en superposition de « A »)

- déplier

Dans le pliage autour de D on obtient le point A’ qui coïncide avec A

SEGMENT :

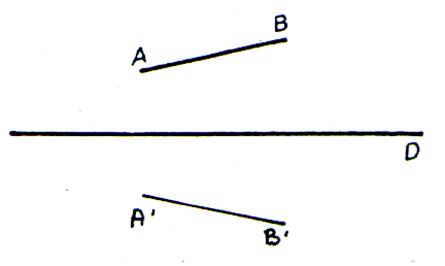
- Activité :

 Placer un point  « A » et un point « B » sur une feuille .(plan). Les joindre par un tracé.

- faire un pli ( le nommer  D ).

- dans un demi plan P placer le segment   « AB » ; à l’extérieur de D.

- replier les demi-plans

-        sur le demi plan P’ dessiner par superposition le segment « AB » , on nommera les points extrêmes  A’et B’.

les segments sont « isométriques »

Dans le pliage autour de « D » on obtient un  segment A’B’ qui coïncide avec le segment AB

Triangle

Activité :

Placer un point  « A » , un point « B »  et un point « C » sur une feuille .(plan). Les joindre par un tracé.

- faire un pli ( le nommer  D ).

- dans un demi plan P placer le Triangle « ABC » ; à l’extérieur de D.

- replier les demi-plans

- sur le demi plan P’ dessiner par superposition le triangle  « ABC » , on nommera les points extrêmes  A’ ; B’ et C’.

Dans le pliage autour de « D » on obtient un  triangle  A’B’C’ qui coïncide avec le triangle ABC

Figure quelconque tracée sur une feuille

Activité :

- Placer un point  « A » , un point « B » , un point « C » et un point « E » , non alignés ,sur une feuille .(plan). Les joindre par un tracé.

- faire un pli ( le nommer  D ).

- vous devez avoir ,dans un demi plan P, placé la figure  « ABCE » ; à l’extérieur de D.

- replier les demi-plans

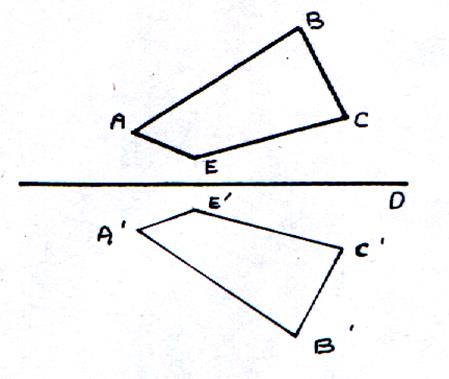
- sur le demi plan P’ dessiner par superposition la figure  « ABCE » , on nommera les points extrêmes  A’ ; B’ ; C’ et E’.

Dans le pliage autour de « D » on obtient une figure  A’B’C’E’ qui coïncide avec une figure ABCE

On peut donc  dire que :

·       Deux figures planes obtenues  , par pliage , l’une par rapport à l’autre sont isométriques .                  

·       Deux figure superposables sont isométriques.

Deux figures F et F’sont en « correspondance biunivoque » si tout point de l’une est associé à un point de l’autre. Si la correspondance respecte toutes les longueurs et les angles, la correspondance est une isométrie.

4 .  Isométrie dans le cercle et le disque

A)  Disques isométriques :

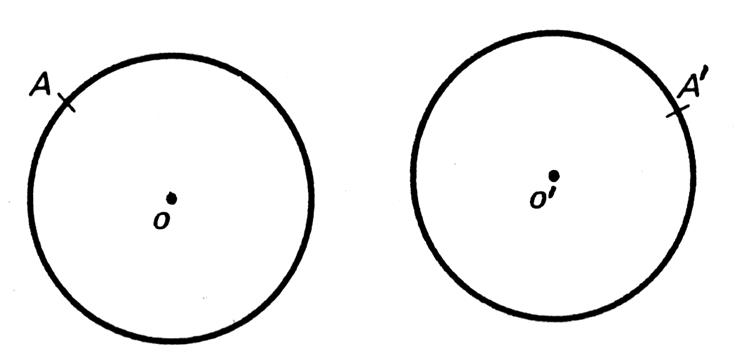
Deux disques de même diamètre ou de même rayon sont « superposable »

Soient deux cercles de centre « O » et « O’ » , « A » un point de la circonférence de « O » et « A’ » un point de la circonférence de « O’ ».

Si « O » vient en « O’ » :

1)     Tout point  « A’ » de « O’ » coïncide avec un point de « O ».

              On peut dire que :  Deux disques de même rayon sont isométriques.

2)     « O » étant maintenu en « O » , nous pouvons faire coïncider les points « A » et « A’ » , « A’ » peut coïncider successivement avec tous les points de « O » , les  circonférences  continuent de coïncider.   

On peut dire que : Un disque peut glisser sur lui - même.

B) Cordes  isométrique d’un disque :

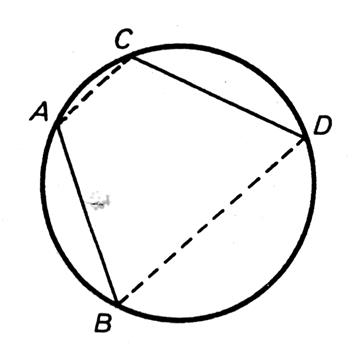
Dans un même disque (ou dans deux disques isométriques) si deux arcs sont isométriques , les cordes  qui  les sous tendent sont également « isométriques » .

La mesure de l’arc AB est égale à la mesure de l’arc CD , ce qui signifie que la longueur de la corde AB est  égale à la longueur de la corde CD.

Question ?

Peut -on trouver un axe de symétrie ?

Que se passe - t- il si nous plions la figure autour de cet axe ?

Remarques complémentaires : les segments AB et CD qui se superposent sont isométriques.

C )  Angles au centre :  (cercle et angle)

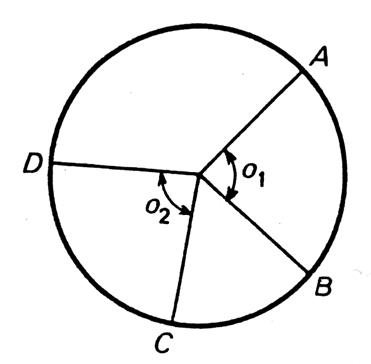
Dans un même disque ( ou dans deux disques isométriques) si des angles au centre sont isométriques , ils interceptent des arcs isométriques.

La mesure de l’angle « O₁ » est égale à la mesure de l’angle « O₂ ».

Ce qui signifie que :

La mesure de l’arc AB est égale à la mesure de l’arc CD , ce qui signifie , aussi, que la longueur de la corde AB est  égale à la longueur de la corde CD.

Remarques :

« Angle au centre » et « arc intercepté »  sont mesurés par le même nombre mais avec des unités différentes.

Les deux triangles AOB et COD  sont isométriques , donc « AB = CD » ce qui confirme que : La mesure de l’arc AB est égale à la mesure de l’arc CD

D )  Cordes  parallèles :

Si une bande coupe une circonférence , ses frontières interceptent des arcs isométriques.

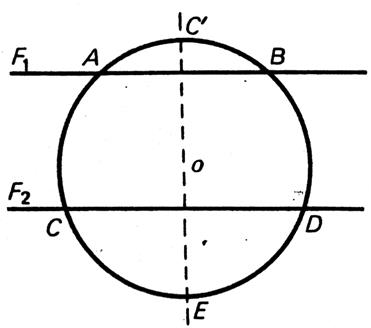
Dans la figure ci contre : lorsque nous menons le diamètre passant par «  C’ O E » perpendiculaire à AB , ce diamètre est aussi perpendiculaire  à « CD »

Le  diamètre «  C’ O E » est l’axe de symétrie .

Par pliage autour de «  C’ O E » on fait coïncider « A » avec « B » et « C » avec « D » , les cordes « AC » et « BD » sont superposables  donc isométriques.

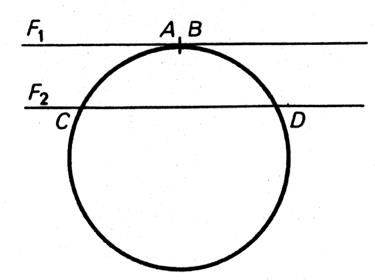
Cas particulier 1 : 

Les cordes « AC » et « BD » sont superposables  donc isométriques

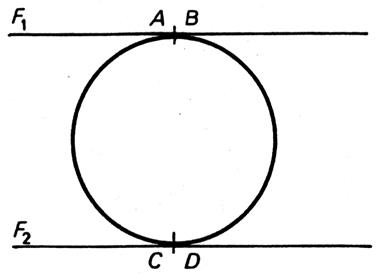
Cas particulier 2

 Les cordes « AC » et « BD » sont superposables  donc isométriques

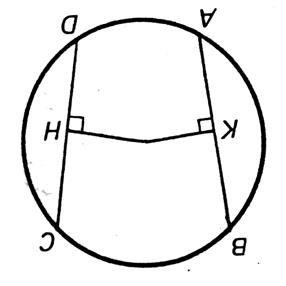
C)      Distance du centre à des cordes isométriques :

Dans un même disque ( ou deux disques isométriques) si deux cordes sont isométriques  elles sont  à égale  distance du centre et réciproquement .

Ainsi  AB = CD et donc  OK = OH

AB et CD étant isométriques  il existe un axe de symétrie passant par « O »

« K » et « H » étant symétriques par rapport à cette axe on en déduit que :

        OK = OH.