|
|
|
LES TRIANGLES homothétiques
Et le rapport d’homothétie
·
TRIANGLES
SEMBLABLES ET HOMOTHETIQUES
·
COTE HOMOLOGUE : (définition)
·
TRIANGLES HOMOTHETIQUES
|
TEST |
COURS |
Interdisciplinarité
|
|
·
TRIANGLES
SEMBLABLES ET HOMOTHETIQUES
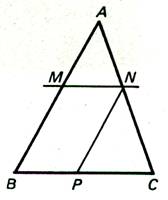
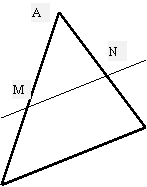
Soit un triangle ABC . Une parallèle au côté BC
coupe AB en M et AC en N .
Menons par N la parallèle à AB qui coupe BC en P .
|
|
|
|
Comparons les triangles ABC et AMN .
Appliquons le théorème de Thalès au triangle
ABC : MN et parallèle à BC .
( 1) ![]()
mais MN
//PB et NP // MB ; nous avons
donc un parallélogramme BNMP
ainsi BP = MN
( à terminer )
|
|
(la
condition de départ : les triangles sont semblables)
On appelle « cotés homologues » de deux triangles , les cotés opposés aux
angles égaux.
(voir
figure ci dessous ; AB et A’’B’’ sont des cotés homologues
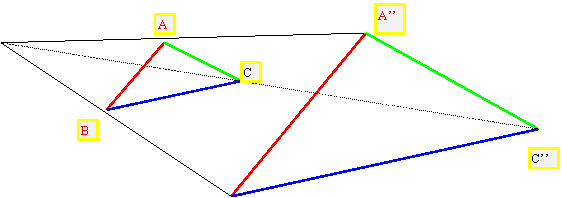
Traçons deux triangles semblables ( ABC
et A’’B’’C’’)en prenant la précaution de tracer les cotés opposés aux angles
égaux , parallèles
|
B’’ |
|||||||||||||
Les cotés homologues
sont :
AB et A’’B’’ (coté opposé à l’angle « C » et
« C’’ ») ;
BC et B’’C’’ , (coté opposé à l’angle « A » et
«A’’ »)
CA et
C’’A’’ (coté
opposé à l’angle « B » et « B’’ »);
Ces cotés sont proportionnels .(faire l’égalité des rapports)
Les angles sont égaux deux à deux .
Les deux triangles sont homothétiques .
·
TRIANGLES
HOMOTHETIQUES
On dit que
deux triangles sont « homothétiques »
si les cotés de l’un sont respectivement parallèles aux cotés de l’autre .
Les angles sont égaux deux à deux ; les côtés
homologues sont proportionnels.
TRIANGLES
HOMOTHETIQUES ET « RAPPORT D ‘
HOMOTHETIE ».
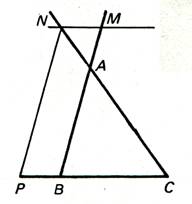
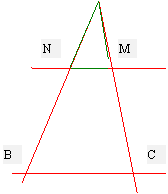
Soit un
triangle ACB ; on trace une droite(
MN ) parallèle à BC ,passant par MN.
Nous obtenons un
« autre » triangle ANM.
Les
triangles ACB et ANM sont semblables et homothétiques (d’après ce qui à été déclaré précédemment )
semblables :leurs angles sont
égaux et leurs cotés sont proportionnels ;et homothétiques :
les cotés opposés aux angles sont tracés parallèles .
|
C B |
||||||||||||||||||||||||||||
Rapport d ’ homothétie
Nous
savons que deux triangles sont homothétiques si leurs cotés homologues sont
proportionnels.
Ainsi AM et AB sont homologues ; AN
et AC sont homologues ; MN et BC sont homologues ; ces cotés
homologues sont proportionnels ; nous pouvons donc écrire l’égalité :
![]() = k
= k
k est appelé « rapport
d’homothétie ».
Ces rapports ont été établis à partir d’un tracé
d’une droite parallèle à un coté d’un triangle ; nous pouvons écrire :
(théorème)
Toute
parallèle à un coté d’un triangle détermine un deuxième triangle homothétique
du premier.
(autre façon de traiter le problème sur le
triangle « coupé » par « une parallèle » à un des
cotés : voir : les projections et
Thalès )
|
E |
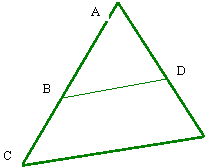
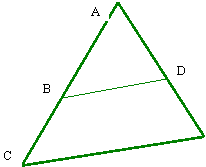
Enoncé :
les triangles
ADB et AEC sont semblables
AD = 27
; DE = 13
BC = 26
; AB = ?
AC = x
; AE = ?
BD = 30 ;
CE =
y
Questions :
1.
Tracer les deux triangles
homothétiques.
2.
Identifier les cotés
homologues ( les nommer deux à deux)
3.
Etablir les rapports d ’ homothétie
4.
Calculer « x » et
« y »
|
E |
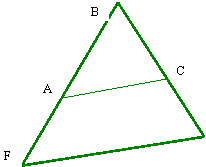
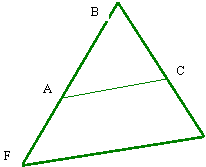
Enoncé :
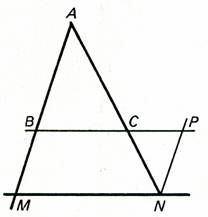
A partir
des triangles semblables et homothétiques AC et FE sont parallèles.
On donne :
AB = 25 ;
AF = ?
BC = ? ;
CE = ?
BF =
40 ; BE =36
AC =
« x » ; FE =
40
Questions et réponses:
1 ) Tracer
les deux triangles homothétiques. ABC
et FBE
2 ) Identifier les cotés homologues ( les nommer deux à deux) :
Attention :pour
nommer un coté et son homologue il faut
choisir le « triangle de départ ou référent » et conserver ce choix
pour nommer les cotés et leur homologue;
je
choisis de prendre le premier triangle
ABC comme « référent » alors pour les trois cas je nomme en premier le coté appartenant au
triangle « référent » :
les
coté AB
et BF sont homologues
les cotés AC et FE sont homologues
les cotés BC et BE sont homologues
3 ) Etablir le rapport d ’ homothétie Lsi l’ordre à été suivi les
rapports s’établissent sans risque d’erreur : ![]() =
=![]() =
=![]()
4 ) Remplacer les lettres par les valeurs
données :
![]() =
=![]() =
=![]()
Calculer « x »
CALCUL : ![]() =
=![]() =
=![]()
Construction particulière se
ramenant à deux triangles homothétiques
Rappel : deux droites
sécantes forment quatre angles ; égaux deux à deux.
Thalès
de Milet : « Travaillant sur les lignes ,fut le premier à
démontrer que deux angles opposés par leur sommet sont égaux.
|
B |
|||||||||||||
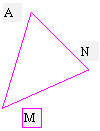
Exemple :
Les
angles A et A’ sont égaux.
Les
angles B et B’ sont égaux.
A
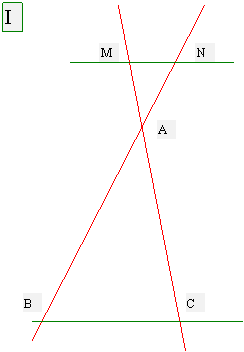
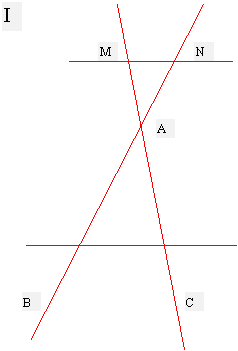
partir de la construction précédente (deux droites sécantes) ,nous traçons deux
parallèles (MN) et (BC) aux deux droites
sécantes en « A » :
|
|
Nous obtenons deux triangles :
AMN
et ACB
Nous pouvons transformer la figure
( I ) ,par rotation autour du point « A » ,pour montrer que
nous avons deux triangles semblables.(voir transformation par rotation autour
de A) )
|
A |
|||||||||||||
Les triangles ANM et ACB sont semblables
donc homothétiques ; Les cotés homologues sont proportionnels, Il suffit d’établir l’égalité des rapports , pour obtenir le rapport
d’homothétie.
|
|
APPLICATION
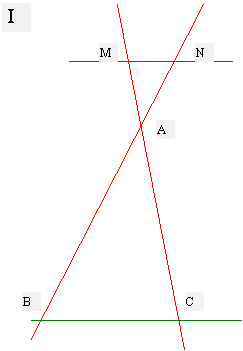
Soit
la figure I
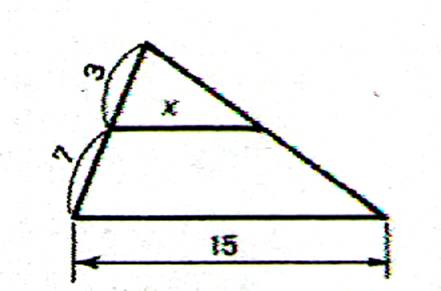
On
donne : AN = 12 cm ;NM = 6cm ;MA = 9 cm ; AC =15 cm .
On nomme AB = « x »
;
BC = « y »
Calculer :
« x » et « y »
Résolution :
les triangles AMN
et ACB sont des triangles semblables :
(l’angle
B et N sont égaux ; l’angle C et M
sont égaux ainsi que l’angle A,)
Nous
pouvons appliquer le théorème lié au rapport d ’ homothétie :
Nous pouvons transformer la figure
( I ) pour montrer que nous avons deux triangles semblables.
|
A |
|||||||||||||
Les triangles ANM et ACB sont semblables
donc homothétiques ; Les cotés homologues sont proportionnels, Il suffit d’établir l’égalité des rapports , pour obtenir le rapport d ’
homothétie.
qui donne : ![]() = k
= k
On remplace les lettres par les données :
![]() = k
= k
Voir Objectif « proportion »des rapports
égaux nous en tirons deux
égalités :
![]() et
et ![]()
Calcul
de « x » : 9x = 15 fois12 ;
« x » = 180 : 9
; « x » = 20 cm
calcul
de « y » : 9y = 15 fois 6 ;
« y » =
90 : 9 ;
« y » = 10 cm
Travaux auto – formatifs :
CONTROLE
1°) Quand dit - on que deux triangles sont
égaux ?
2° ) Quand dit - on que d’eux triangles sont
isométriques ?
3° ) Compléter la
phrase : deux triangles sont dits
semblables si :.............................................
4° ) Qu’appelle -t - on
« cotés homologues » ?
5° ) Quand dit - on que
deux triangles sont homothétiques .
6° )Compléter la phrase
suivante :
Toute parallèle à un
coté d ’ un triangle détermine
.............
7°) Qu’est
qu ‘un rapport d ’ homothétie .(aidez vous d’ un exemple )
1°) Tracer un triangle quelconque (ni
rectangle ; ni isocèle) ; ensuite tracer le triangle égal au
précédent et un triangle isométrique.
2° ) Les angles d’un triangle mesurent 43° et 54°
.Construire un triangle « isométrique ».
3° ) Les angles A et B d’un triangle ABC mesurent
43° et 54°,on donne BC = 40 mm Construire un triangle A’B’C’ semblable
.avec B’C’ = 55mm
4°) On donne deux droites sécantes coupées par deux
droites parallèles passant par MN et BC
On donne : AN = 12 cm ;NM = 6cm ;MA = 9 cm ; AC =15
cm .
On nomme AB =
« x » ;
BC = « y »
Calculer :
« x » et « y »
C B A |
TRIANGLES HOMOTHETIQUES EXERCICES RESOLUS :
|
E |
Enoncé :
les
triangles ADB et AEC sont semblables
AD = ;
DE =
BC = ; AB
=
AC = ; AE
=
BD = ; CE
=
Questions :
1.
Tracer les deux triangles
homothétiques.
2.
Identifier les cotés
homologues ( les nommer deux à deux)
3.
Etablir le rapport
d’homothétie
4.
Calculer « x »
|
E |
Enoncé :
A partir
des triangles semblables et homothétiques LAC et
FE sont parallèles.
On donne :
AB =
; AF =
BC =
; CB =
BF = ;
BE =
AC =
; FE =
Questions :
1.
Tracer les deux triangles
homothétiques.
2.
Identifier les cotés
homologues ( les nommer deux à deux)
3.
Etablir le rapport
d’homothétie
4.
Calculer « x »
|
Calculer « x » |
|