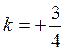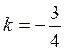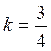Pré requis:

Isométrie
Rotation
Homothétie

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : 1°) Les triangles semblables 2°) Les translations(notion) .

Objectif suivant : Les transformations géométriques

1°) tableau 2°) liste des cours en géométrie

DOSSIER : SIMILITUDE (semblable)

1. Définitions et propriétés générales

2. Rapport de similitude ou « ECHELLE » : avec une figure géométrique , un triangle.

3. Exemples de figures semblables .

4. Similitude par glissement.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Définitions et propriétés générales

1°) Définitions

Deux figures sont dites semblables si l’une d’elle est égale à une homothétie de l’autre .

Pour rendre homothétique deux figures semblables , il faudra imprimer à l’une d’elle soit un glissement soit un retournement : d’où la similitude par glissement et la similitude par retournement.

2°) Rapport de similitude ou « ECHELLE »

Deux figures semblables données pourrons être rendues , au choix , homothétiques positives ( rapport par exemple) ou homothétiques négatives . Le nombre pris en valeur absolue s’appelle « rapport de similitude » ou « échelle ».

Forme d’une figure. F

Deux éléments importants la caractérisent :

1°) les angles de configuration , c’est à dire les angles A , B , C , formés par ses divers droites ;

2°)les rapports de configuration, c’est à dire les rapports , …formés par ses divers segments .

Or , dans deux figures homothétiques , et aussi par conséquent dans deux figures semblables F et F₁ (notamment dans deux polygones )

1°) les angles de configuration homologues sont égaux : l’angle A = l’angle A₁ ; l’angle B = l’angle B₁ ….

2°) les segments homologues étant proportionnels , puisque l’on a toujours :

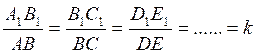, l’on en déduit ,

par exemple : 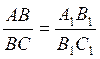, c’est à dire que dans l’une et l’autre figure , les rapports de configuration homologues sont égaux.

Remarques :

1°) ces propriétés justifient le nom de similitude donné à cette transformation , puisqu’elle conserve la forme de la figure.

2°) Dans l’ homothétie , les segments homologues sont de plus, parallèles.

3°) Dans l’égalité , le rapport k est égal à 1 , et les segments homologues sont égaux.

CAS de similitude.

Polygones en général .

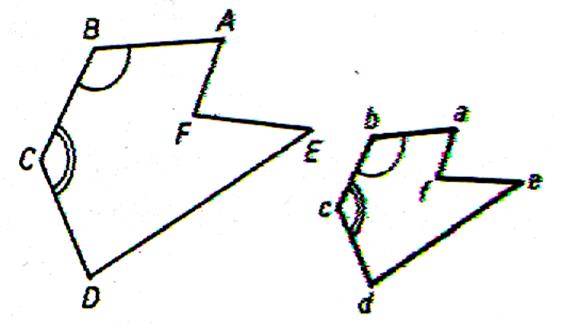
Si deux polygones convexes , ABCDE , A₁B₁C₁D₁E₁ ont les angles aux sommets homologues égaux et les côtés homologues proportionnels , c’est à dire si l’on a , k étant un nombre fixe :

L’angle A₁ = l’angle A , l’angle B₁ = l’angle B ,

A₁B₁ = k. AB , B₁C₁ = k .BC

Ces deux polygones sont semblables .

En effet , au polygone P faisons subir une homothétie de rapport K . Il se transforme en un polygone P’ pour lequel on a :

L’angle A’ = l’angle A ; L’angle B’ = L’angle B

A’B’ = k.AB ; B’C’ = k.BC….

P’ et P₁ ont donc les angles homologues égaux et les cotés homologues égaux donc sont évidemment superposables . P₁est donc égal à P’ , homothétique de P.

Remarques .

1)) cette démonstration peut s’étendre à des polygones concaves ou enchevêtrés pourvu que les angles homologues soient de même sens .

2°) Ce théorème étant réciproque de celui qui découle de la première définition (Deux figures sont dites semblables si l’une d’elle est égale à une homothétie de l’autre .), son énoncé peut être pris aussi comme définition des polygones semblables .Toutefois , une rel

marque s’impose . Partons de ABCDE et , conformément à cette seconde définition , construisons successivement :

A₁B₁ = AB et l’angle B₁= l’angle B ; B₁C₁ =BC et l’angle C₁= l’angle C jusqu’à D₁E₁ = DE .

Arrivés là , si nous traçons l’angle E₁ = l’angle E , qui nous dit que la chaîne de fermera en A₁ et que l’on aura aussi E₁A₁ = EA ?

L’existence de polygones semblables , quand on part de cette seconde définition , n’est pas évidente ; au contraire la première définition , basée sur l’homothétie est constructive , et l’on ne peut guère s’en dispenser.

3°)Ajoutons que cette seconde définition ne vaut que pour les polygones et ne s’étend pas aux lignes courbes.

Avec les TRIANGLES :

« pour en savoir plus ! ! ! »

Pour deux triangles ABC , et A₁B₁C₁ , il n’est pas nécessaire de connaître les 5 égalités

L’angle A = l’angle A₁ l’angle B = l’angle B₁ l’angle C = l’angle C₁ ;

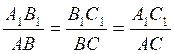pour conclure à leur similitude. Deux suffisent , convenablement choisies.

Premier cas : si T et T’ ont deux angles égaux : A = A₁ et B = B₁ , ils sont semblables.

En effet , au triangle T faisons subir une homothétie de rapport k =  ; T se transforme en triangle T’ où l’on a : l’angle A’ = l’angle A , l’angle B’ = l’angle B

et A’B’ = k.AB ; donc T’ et T₁ ont un coté égal A’B’ = A₁B₁ bordé par deux angles égaux ; T₁ est donc égal à T’ , homothétique de T.

Deuxième cas . si T et T₁ ont un angle égal A = A₁ bordé par deux cotés proportionnels A₁B₁= k . AB et A₁C₁ = k . AC ils sont semblables .

Une homothétie de rapport k transforme T en un triangle T’ où : l’angle A’ = l’angle A , A’B’ = k.AB , A’C’ = k.AC ; donc T’ et T₁ ont un angle égal bordé par deux cotés égaux ; T₁ est donc égal à T’ , homothétique de T.

Troisième cas : Si T et T₁ ont les cotés proportionnels : A₁B₁= k . AB et A₁C₁ = k . AC ; B₁C₁= k . BC , ils sont semblables .

Une homothétie de rapport k transforme T en un triangle T’ égal à T₁ comme ayant les trois cotés égaux .

Remarques :

Pour les deux premiers cas , on peut aussi , profitant de l’angle égal A = A₁ , loger les deux triangles l’un dans l’autre et utiliser le théorème de Thalès.

Cela revient , dans les démonstrations qui précèdent , a prendre l’angle A pour centre d’ homothétie .

3°) Autres cas de similitude .

Si deux triangles rectangles en A et A₁ ont deux cotés proportionnels A₁B₁= k . AB et B₁C₁= k . BC ils sont semblables . Car une homothétie de rapport « k » transforme « T » en un triangle « T’ » , égal à « T₁ «  comme rectangle , ayant l’hypoténuse égale et un autre coté égal .

Ou , ce qui revient au même , si deux triangles rectangles ont un rapport de configuration égal , par exemple 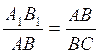ils sont semblables .

2°) Si dans deux triangles ABC et A’B’C’ les droites AB et A’B’ ; AC et A’C’ ; BC et B’C’ , font le même angle a en grandeur et en sens , ces deux triangles sont semblables par glissement .

Car une rotation d’angle a transformera T en un triangle T’ , homothétique de T₁ comme ayant les cotés parallèles .

En particulier , si deux triangles ont les cotés perpendiculaires , ils sont semblables.

3°) deux polygones homothétiques , et aussi par conséquent deux polygones semblables , sont décomposés par leurs diagonales homologues en triangles semblables.

Réciproquement , si deux polygones sont formés par des juxtapositions dans le même ordre de triangles semblables deux à deux , ces deux polygones seront semblables , car ils auront les angles homologues égaux ( sommes des angles de ces triangles ) , et les cotés homologues proportionnels ( cotés de ces triangles se trouvant en bordure ).

Généralisation .

L’on peut démontrer que :

1°) Si dans deux figures F et F₁ tous les angles de configuration homologues sont égaux ( angles des cotés , des diagonales , etc. ) cela suffit pour que les deux figures soient semblables.

(en effet , il n(est même jamais besoin de connaître l’égalité de tous les angles , un certain nombre d’égalités convenablement choisies suffisent pour entraîner les autres .)

La démonstration est analogue à celle du premier cas de similitude des triangles.

2°) Si dans deux figures F et F₁ , tous les rapport de configuration homologues sont égaux , cela suffit pour que les deux figures soient semblables.

Exemples de figures semblables :

En partant soit de la première , soit de la deuxième définition , on obtiendra comme figure semblable :

1°) D ’ un polygone régulier ( cotés égaux , angles égaux ) un autre polygone ayant les mêmes propriétés , donc un polygone régulier de même espèce :

2°) D ’un rectangle R , un autre rectangle R’ ayant les mêmes angles des diagonales , et même rapport entre les deux dimensions.

3°) D ’un triangle isocèle , un autre triangle isocèle ayant même angle au sommet ( exemple :triangle rectangles isocèles ).

4°) D ’un losange L , un autre losange L’ ayant même angles aux sommets , et même rapport entre les deux diagonales.

5°) D ’un demi -triangle équilatéral , un autre triangle de même espèce .

6 °)D’un arc de cercle AB , un autre arc de cercle A’B’ ayant même angle au centre.

Toutes les réciproques sont vraies : deux figures ayant l’une des propriétés qu’on vient d’indiquer sont semblables.

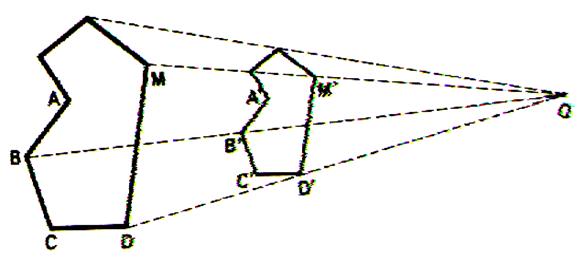
Similitude par glissement.

Soient deux figures « F » et « F₁ » semblables par glissement.

Si elles sont homothétiques , le centre d’homothétie « O » occupe une position homologue , c’est un point double , dans l’une et l’autre .

Si elles ne sont pas homothétiques , cherchons si elles n’auraient pas cependant un point double « O » : car si nous trouvions un tel point , nous pourrions d’abord , par une homothétie de centre O et de rapport convenable , amener F en une position intermédiaire F’ ;

Ensuite , par une rotation de centre « O » , d’angle convenable , amener F’ en sa position définitive F₁.

Travaux auto formatifs.

CONTROLE:

aucun

EVALUATION:

Aucune !