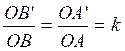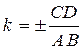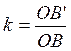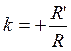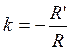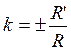Pré requis:

Les figures géométriques élémentaires

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : Les transformations en géométrie

Objectif suivant 1°) les transformations. 2°) Les triangles homothétiques 3°) « vecteurs » et « homothétie »

Liste de cours sur la géométrie plane.

DOSSIER : HOMOTHETIE

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Définition
Etant donné un point fixe O appelé centre d’homothétie , et un nombre fixe « k » appelé rapport d’homothétie : soit A un point quelconque ; sur la droite OA prenons le point A’ défini par l’égalité = k Le point A’ sera dit homothétique de A ( centre O , rapport k ) K peut être positif ou négatif ; K peut être > 1 , <1 , =1 (voir : échelle)

Homothétiques des figures usuelles

Droite .

1°) Une droite D passant par le centre O a pour homothétique la droite elle même.

2°) Soient deux droites ne passant par O ; A et B deux points de D ; A’ l’homothétique de A . Par A’ menons D’ parallèle à D ; la droite OB coupe D’ en un point B’ :

le théorème de Thalès donne :

,

donc B’ est l’homothétique de B , et : l’homothétique de la droite D est une droite D’ parallèle à D.

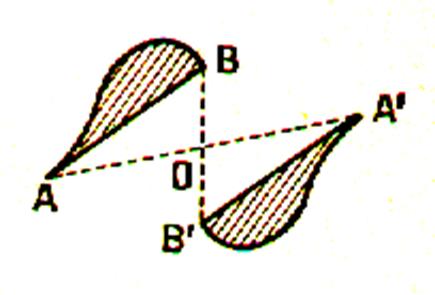
3°) Si D est orientée , D et D’ seront de même orientation ou d’orientations contraires suivant que l’homothétie est positive ou négative ( c’est à dire k >0 ou k < 0 .

4°) Un vecteur AB a pour homothétie un vecteur parallèle A’B’ , tel que

= k

ANGLE :

L’homothétie d’un angle est un angle égal et de même sens de rotation , même si l’homothétie est négative.

Polygone .

D’après ce qui précède , l’homothétie sera un autre polygone ; les deux polygones homothétiques auront :

1°) les angles homologues égaux et de même sens A’ = A ; B ’= B

Les cotés homologues parallèles et proportionnels :

= k  ; = k , etc…

Pour construire l’homothétique de ABCDEF , on joint le centre à tous les sommets , on construit l’homothétique de A ; puis on mène parallèle à , ’ parallèle à , etc . ; comme on aura , de proche en proche = k , etc. On est sûr que la chaîne se fermera et qu’on sera ramené au point A.

Cercle :

Soit le cercle ( C) de rayon ( R) .Construisons C’ homothétique du centre C ; un rayon CM aura pour homothétique :

’ = k = k R ,

ce vecteur est donc constant .

L’ homothétique du cercle ( C) sera le cercle ( C’ ) de rayon R’ = k R

Réciproques .

1°) Droites :

deux droites parallèles sont homothétiques d’une infinité de manières ; le centre d’homothétie peut être pris n’importe où sauf sur une des deux droites , le rapport d’homothétie peut-être un nombre quelconque mais il dépend du centre choisi.

2°) deux vecteurs parallèles et  non équipollents sont homothétiques ; le centre O est l’intersection des droites AA’ et BB’ ; le rapport est k =

3°) deux segments parallèles AB et CD sont homothétiques ; de deux manières s’ils ne sont égaux ; les centres P et N étant les point d’intersection de AC et de BD , ou bien de AD et de BC ; les rapports sont opposés.

Triangles	En plus ++++
Deux triangles ABC et A’B’C’ dont les cotés sont parallèles mais non équipollents , sont homothétiques . Soit O le point d’intersection de BB’ et CC4 ; avec O comme centre , et le rapport , construisons l’homothétique de ABC suivant la méthode donnée pour les polygones ; nous retrouvons précisément A’B’C’.

Cercles :

Soient deux cercles inégaux et non concentriques . Menons deux rayons CM et C’M’ parallèles et de même sens ; les droites CC’ et MM’ se coupent en P ; avec le point P comme centre et le rapport construisons l’homothétique de ( C ) par la méthode (SOS ) , nous retrouvons précisément ( C’ )

Raisonnement analogue en partant de deux rayons parallèles de sens contraires , avec le rapport

Deux cercles inégaux et non concentriques sont homothétique dans deux homothéties de rapports les centres d’homothétie P et N sont deux points conjugués harmoniques par rapport aux centres C et C’ des deux cercles.

En particulier si les deux cercles sont tangents , leur point de contact est l’un des centres d’homothétie.

2°) pour deux cercles concentriques ces deux homothéties de rapport , subsistent , mais les deux centres d’homothéties P et N se confondent avec le centre C des deux cercles.

3°) pour deux cercles égaux , une seule homothétie subsiste ( de rapport –1 : c’est une symétrie ) , l’autre n’existe plus et se trouve remplacée par une translation .

TRAVAUX AUTO FORMATIFS.

CONTROLE:

EVALUATION: