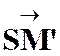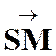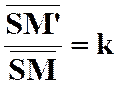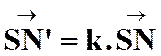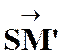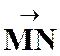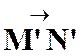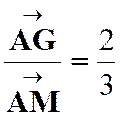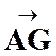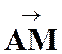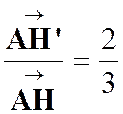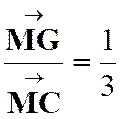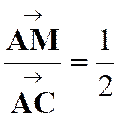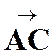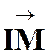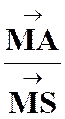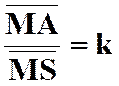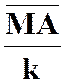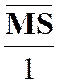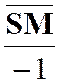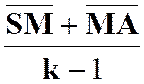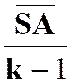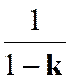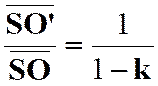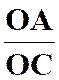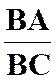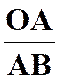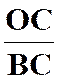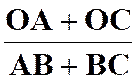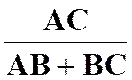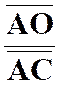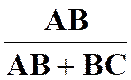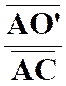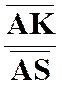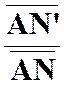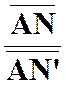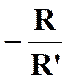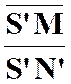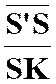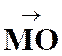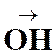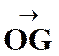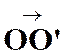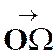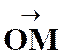Définition de l’homothétie .

« homothétie »  et  la recherche des lieux géométriques.

Représentation graphique de l’homothétie  d’une figure géométrique .

·      Et   des  problèmes …

COURS

Définition :

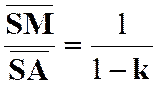
La correspondance entre le point « M ’ » et un point « M » , par homothétie ,relatif à un centre « S » et dans un rapport « k » est définie par l’égalité vectorielle :

 = k .  avec k 0 et k 1   ( « k » est un nombre algébrique ) .  ( relation 1 )
qui signifie à la fois que :

Les points « S » , « M » et « M ’ » sont alignés.

info : homothétie et représentation graphique.

De l’égalité ( 1 ) découle immédiatement la propriété fondamentale de l’homothétie.

Si on envisage deux couples de points homologues « M » et « M ’ », « N » et «  N ’ », on a à la fois ( 1 ) et :                     (relation 2)

Mais (relation 2) peut s’écrire : 

 +   =  k  .  (   + )                        ( relation 3)

Ce qui peut se réduire (voir relation 1)

à     =  k ( )                       ce qui donne ci -contre la ( relation 4)

Représentation graphique de l’homothétie  d’une figure géométrique .

C’est ainsi que les vecteurs définis par deux couples de points homologues sont « parallèles » et le rapport de leurs mesures algébriques est égal au « rapport d’homothétie ».

Il en résulte que  :

·      la figure homothétique : D’une droite est en général une droite parallèle.

·      la figure homothétique : D’un plan est en général un plan parallèle.

·      la figure homothétique : D’un angle est un angle égal.

·      la figure homothétique :  D’un dièdre est un dièdre égal.

·      la figure homothétique :  D’un cercle est un cercle.

·      la figure homothétique :  D’une sphère est une sphère.

Et aussi que les tangentes en deux points homologues de deux courbes homothétique existent simultanément et sont parallèles.

D’ où :   L’homothétie conserve les angles et les contacts.

« homothétie »  et  la recherche des lieux géométriques.

Commentaire : l ’homothétie est un procédé pour la recherche des lieux géométriques.

Quand, dans ce but , on aura utilisé l’homothétie, il ne sera pas nécessaire d’établir une réciproque , parce que l’homothétie donne une correspondance « point par point ». Si le point « M » décrit complètement l’arc « AB » d’une courbe ( L ) , le point homologue «  M ’ » décrit complètement l’arc correspondant «  A ‘ B ’ »de la courbe homothétique ( L’ ) .   

PROBLEMES :

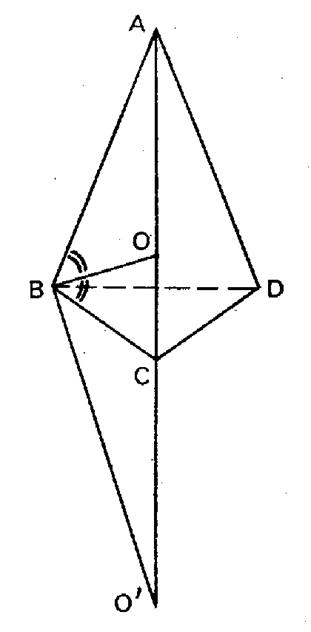
Problème 1 :

Un triangle « ABC » a un sommet fixe « A » . Le support du côté « BC » est une droite fixe ( ). Lieu géométrique du point de concours « G » des médianes de ce triangle, quand les points « B » et « C » se déplacent arbitrairement sur ( ).

Solution :

Désignons par « M » le milieu du côté « BC » . On sait que le point de concours « G » des médianes est tels que :    ou   =  .

Donc « G » correspond à « M » dans l’homothétie de centre « A3 et de rapport :

Le lieu du point « G » est la   droite ( ’ ).parallèle à  ( ). Et qui , par exemple , coupe «  H ’ » la hauteur «  A H » , « H ’ » étant tel que :   

Problème 2 :

Deux points « A » et « B » sont fixes ; le point « C » décrit soit une droite ( )  soit un cercle ( ) . Lieu du point de concours « G » des médianes du triangle « ABC ».

Indications : le milieu « M » de « AB » est fixe et : ,, »  G » correspond à « C » dans l’homothétie de centre « M » et de rapport :

Problème 3 : 

Le sommet « A » d’un carré « ABCD » est fixe. Le centre « O » du carré décrit un cercle ( ) .Lieu géométrie  du sommet « C » opposé à « A » par rapport  à « O » . Mise en place de ce lieu .

Cours suite 1 : Parfois la solution met en jeu plusieurs homothéties.

Problème 4 : 

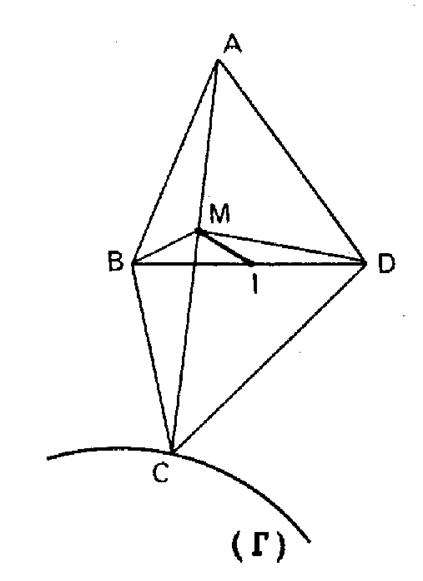
Soit « ABCD » un quadrilatère plan. Les sommets « ABD » sont fixes et le point « G » décrit une courbe donnée ( )Soit « M » le milieu de « AC » . Lieu géométrique du point de concours « G » des médianes du triangle « BMD ».

Solution :

Le point « A3 étant fixé et « M » le milieu de « AC »   ou  =

Le lieu de « M » est la courbe (  ‘ ) homothétique  de   ( ) relativement  au centre « A » et dans le rapport .

« B » et « D »  étant fixes , le milieu « I » de « BD » est fixe et comme :  =  

Le lieu de « G » est la courbe ( ’ ‘ ) déduite de  ( ‘ ) dans l’homothétie de centre « I » et de rapport  .

Problème 5 : 

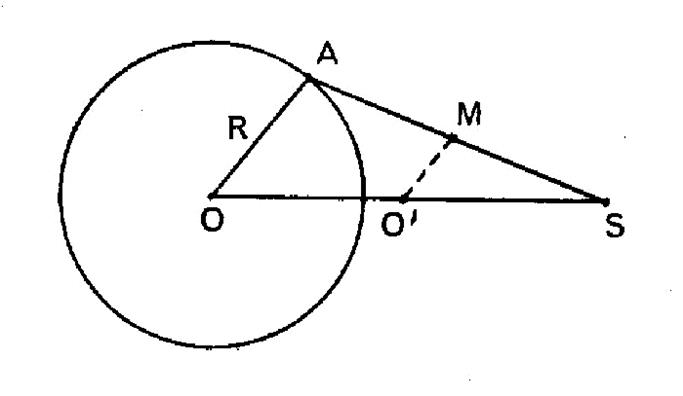
On joint un point fixe « S » au milieu de « M » du rayon variable « OA » d’un cercle donné. Lieu du point « P » qui divise  de tel sorte que  = k .  ; « k » est le rapport algébrique donné.

Indications conduisant à la solution : Le lieu de « M » est homothétique de celui de « A » relativement au point « O » dans le rapport    . Le lieu de « P » se déduit de celui de « M » par homothétie de centre « S » et de rapport « k ».

On pourrait généraliser  en supposant que « M » divise « OA » dans un rapport donné «  ». 

Info :  Dans les exemples précédents , le rapport à utiliser et l’homothétie associé étaient immédiatement en évidence, il n’en est pas toujours ainsi et l’on doit parfois opérer quelques transformations de calcul.

Problème 6 : 

Soit « S » un point fixe . Le point  « A » décrit un cercle donné  ( C ) .Lieu du point « M » tel que « = k »

Solution : Remarquons que la relation algébrique :   peut s’écrire :

= =  = =

On en déduit      et « M » correspond à « A » dans l’homothétie de centre « S » et de rapport :

Remarque : On pourra marquer le centre « O’ » du cercle lien de « M » en menant par l’une des propositions « M » la parallèle « MO’ » à « AO »

D’ailleurs :

Problème 7 : 

Les côtés adjacents d’un quadrilatère sont égaux deux à deux. Montrer que les supports des côtés de ce quadrilatère sont tangents à deux cercles.

Lieux géométriques des centres de ces cercles, lorsque le quadrilatère se déforme, l’un des côtés restant fixe.

Solution :

Par hypothèse «  AB = AD » et «  BC = CD »

La droite « CA » est bissectrice des angles   et     , puisqu’elle est médiatrice de « BD ». ( lieu des points équidistants  de « B » et « D »).

La figure étant symétrique par rapport à « AC » , les bissectrices de « B » et « D » coupent « CA » aux mêmes points « O » et « O’ »qui , étant équidistants des quatre côtés du quadrilatère, sont les centres « O » et « O’ » de cercles tangents à ces quatre côtés.

Supposons que « AB » soit le côté fixe. Le point « C » décrit le cercle ( L ) de centre « B » et de rayon « BC ».

Le théorème de la bissectrice , appliqué au triangle « ABC » donne :

 =   d’où :

= =  =   ;       de cette suite de rapports , on déduit : =  et ceci montre que le lieu du point  ( O ) est le cercle ( L’ ) déduit  du cercle  ( L’ ) lieu de  «  C » par l’homothétie de centre « A » et de rapport :

                                      On montrera  de même que :   =        (  A B > BC )  donc que le lieu de «  O ‘ » est le cercle ( L’ ) déduit de ( L ) par homothétie  de centre « A » et de rapport  

Problème 8 : 

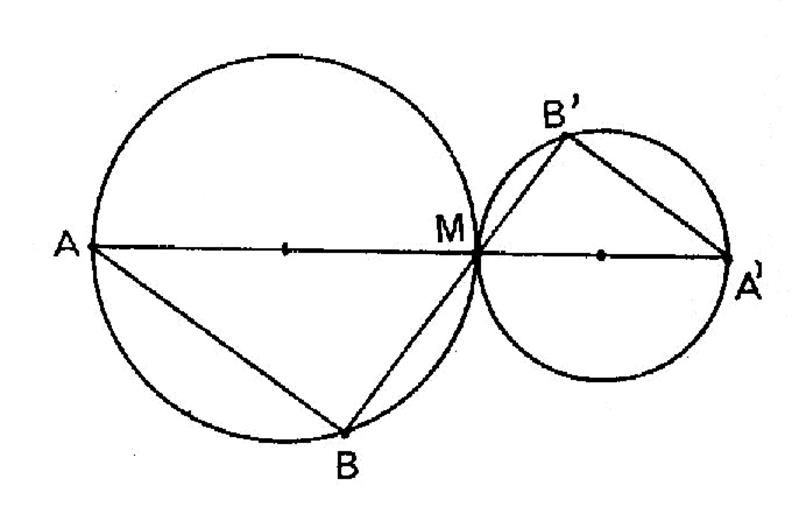
Par le point de contact de deux cercles tangents on mène deux transversales qui coupent respectivement en « A » et « A’ » ; « B » et « B’ » . Démontrer que les cordes  « AB » et « A’B’ » sont parallèles  et calculer le rapport de leurs longueurs.

Solution :

Les deux cas de figure correspondent à la nature du contact  des deux cercles. Mais dans les deux cas, les cercles sont homothétiques par rapport au point « M ».

Les cordes « AB » et « A’ B’ », éléments linéaires homologues, sont parallèles et leur rapport est égal au rapport d’homothétie des deux cercles, qui est celui de leurs rayons. ( théorème fondamental « relation 4 » du cours) 

Cas 1

Cas 2 :

Problème 9 : 

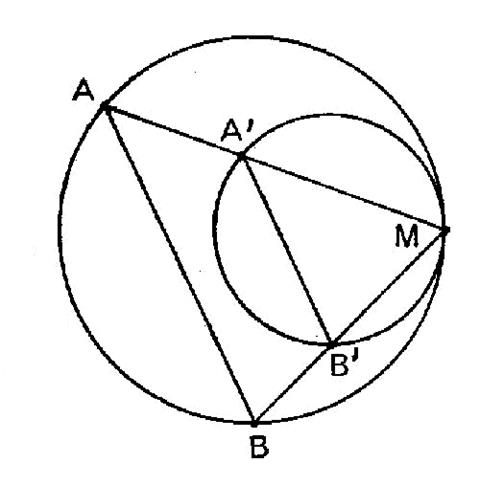
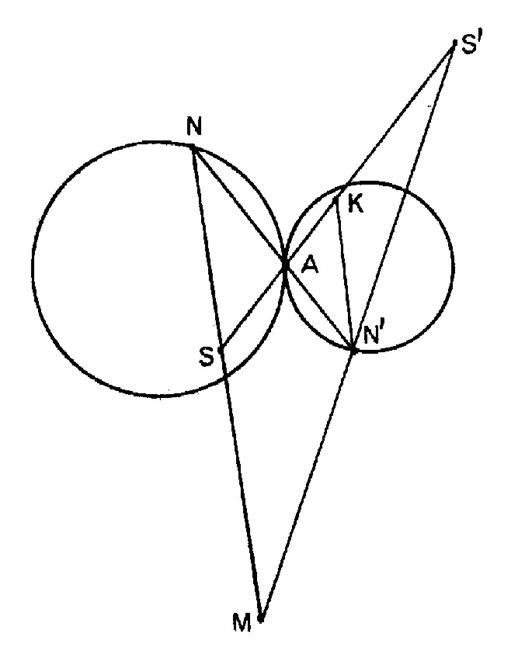
Deux cercles ( C ) et ( C’) de rayons respectifs « R » et « R’ » sont tangents extérieurement en « A ». Sur une transversales fixe passant par « A » on marque deux points fixes « S » et « S’ ». Une transversale mobile passant  par « A » coupe les cercles respectivement en « N » et « N ’ » .

Les droites « NS » et « N’ S’ » se coupent en « M ». Lieu du point « M ».

Solution :

Menons par «  N ’ » la parallèle à « SN » qui coupe la droite fixe «  S S’ » en « K ».

Les triangles « A K N’ » et « ASN » sont homothétiques par rapport à « A » et :

=       ( relation 1 )

Mais les cercles étant homothétiques par rapport à « A » :

=         ( relation 2 )

donc :

=         ( relation 3)  et par conséquent le point « K » est fixe.

Mais les triangles  «  S’ K N’ » et  « S S4 M » sont homothétiques par rapport à «  S’ »  et donnent :  =         ( relation 4).

Le lieu de « M » est donc l’homothétique du cercle ( C’) lieu de « N’ » relativement au centre «  S’ » et dans le rapport :

Problème 10 : 

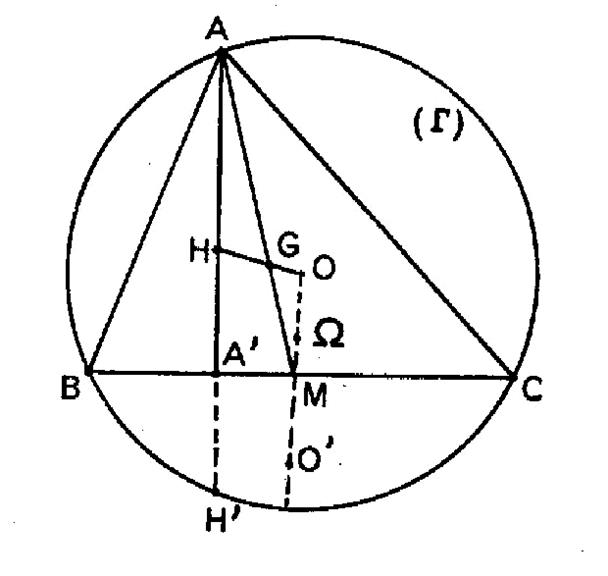
Un triangle « ABC » est inscrit dans un cercle fixe ( ) de centre ( O) . Les points « B » et « C » sont fixes. Le point « A » décrit tout le cercle.

Lieux géométriques du centre de gravité « G »  et de l’orthocentre du triangle.

Solution :

Le milieu « M » de « BC » est fixe.

 Le centre de gravité « G » est tel que :  = .

 Le lieu de « G » est donc le cercle ( ‘ ) déduit de  (  ) dans l’ homothétie de centre « M » et de rapport :

Le centre  de ce cercle est sur « OM » tel que :   3  =   et son rayon est le tiers de celui de (  ).

Mais d’après la propriété du segment d’Euler :   =  3 .

Le lieu de « H » se déduit du lieu de « G » par homothétie de centre « O » et de rapport « 3 ». Le rayon du cercle trouvé est le triple de celui de ( ‘ ) donc égal à celui de (  ). Son centre est le point « O’ » tel que :  =  3  = 2 

Et   « O ‘ » est le symétrique de « O » par rapport à « BC ».

Remarque : On peut dire que cette conclusion était pré »visible puisque le symétrique de l’ orthocentre « H » par rapport à « BC» appartient au cercle circonscrit au triangle « ABC » .

Le  lieu « H » est le cercle ( ‘’ ) symétrique de (  ) par rapport à « BC ».

( rédigé : le 5 novembre 2013)

TRAVAUX AUTO FORMATIFS.

CONTROLE

EVALUATION.

Refaire les problèmes…du cours  …… ;;;;