Pré requis:
|
|
|
|
|
|
|
|
|
|
direction |
Environnement du dossier:
|
Objectif précédent : 1°)le cheminement
dans un plan |
Tableau Classe :CM ;….. |
DOSSIER « géométrie « : LA TRANSLATION :
NOTIONS dans un plan ;travaux
sur quadrillages
|
TEST |
COURS |
Interdisciplinarité |
|
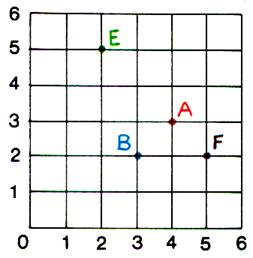
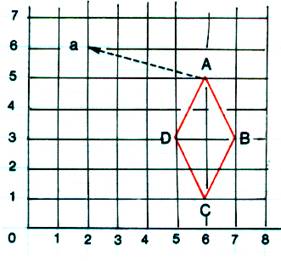
Les coordonnées d’un point :
|
La position de point E par rapport au point
« 0 » dans le quadrillage
est déterminée par les nombres 2 et 5 ; et non pas 5 et 2
, par convention nous avions choisi de lire ( droite ou gauche
et haut ou bas ) On notera : E ( 2 ;5) De même : B ( 3 ; 2 ) A ( 4 ; 3 ) F ( 5 ; 2 ) |
|
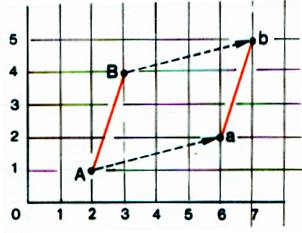
I ) Translation d’une droite :
|
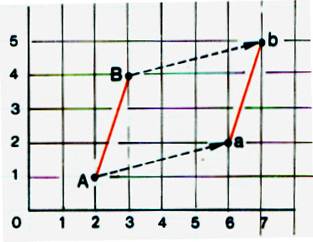
Un déplacement de 4 pas à droite et 1 pas en haut est codé 4d 1h Si le point A va en « a » A !’ 4d 1h!’ « a » Si le point B va en « b » B !’ 4d 1h!’ « b » Les deux points ont le même déplacement. AB = ab |
|
|
On dit que : [ab] est parallèle à [AB] [ab] est
« l’image » de [AB] par la translation !’ 4d 1h!’ |
|
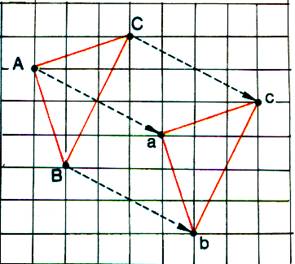
II
) Translation d’un triangle :
|
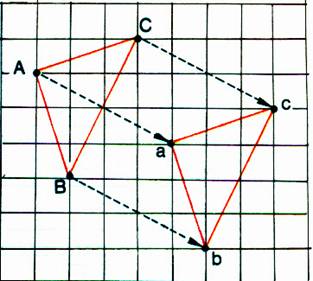
Le triangle abc est l’image du triangle ABC par la translation !’ 4d 2b!’ Ces 2 triangles sont superposables . |
|
ACTIVITES :
N°1
|
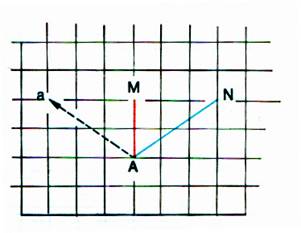
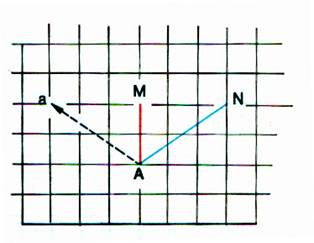
Sur du papier quadrillé ,
marquer les points A , M , N puis
tracer les deux segments [AM] et [AN]. a) Effectuer pour le point A , un déplacement de
3g et de 2 h ; on obtient le point « a » b) Effectuer le même déplacement ( 3g ; 2h)
pour le point M puis pour le point N ,
on obtient les points « m » et « n » |
|
|
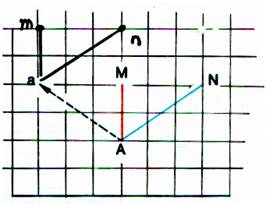
Joindre « am »
et « an » Observer les segments [AM] et [am] ;
comparer leur longueur et leur direction ;
Faire de même avec les segments [AN] et
[an]. |
|
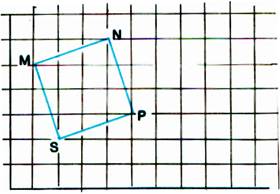
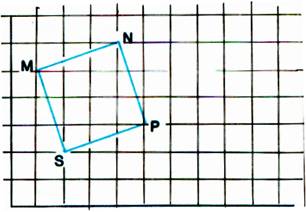
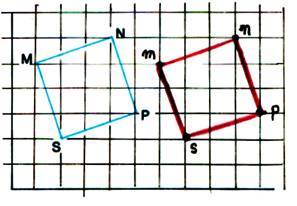
II) Sur papier quadrillé , placer
les points M , N , P , S ; les joindre pour former un carré.
|
Effectuer pour chacun des 4 sommets le
déplacement ( 5d ;1b). Joindre les 4 points m ,
n, p, s , obtenus . Comparer la figure mnps au carré MNPS |
|
III)
|
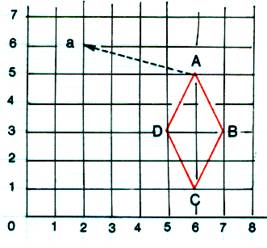
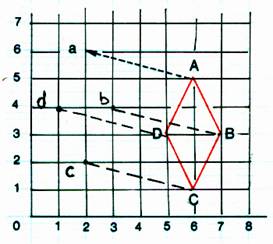
Sur un papier quadrillé ,
reporter les points : A ( 6 ;5) B ( 7 ;3 ) C ( 6 ; 1) D ( 5 ; 3 ) a) Trouver la nature du quadrilatère ABCD b) Effectuer pour chacun des 4 sommets le déplacement (4g ; 1h) et
trouver les codes des points « a » ,
« b » , « c » , « d » obtenus. |
|
|
Tracer les segments : [Aa] ;
[B b ] ; [ C c ] ; [ D d ] ; comparer les longueurs et les directions de
ces 4 segments |
|
IV)
|
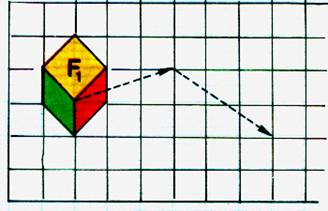
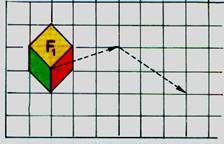
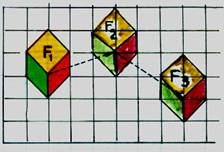
Sur un papier quadrillé ,
reproduire la figure F1. a) Effectuer tous les points de cette figure la
translation de code ( 3d , 1h) puis tracer la figure
F2 obtenue . |
|
|
Effectuer maintenant ,
pour tous les points de cette nouvelle
figure , le déplacement ( 3d ; 2b) et tracer la figure F3 obtenue . Donner le code de déplacement qui permet
d’obtenir directement la figure F3 à partir de la figure F2 . |
|
TRAVAUX AUTO FORMATIFS.
1°) définition d’une
translation :
EVALUATION :
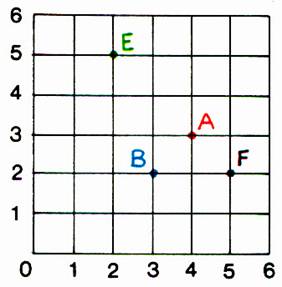
1°) Donner les coordonnées des points A ; B ; E ;F
|
|
|
2° Compléter les phrases :
|
Un déplacement de 4 pas à droite et 1 pas en haut est codé 4d 1h Si le point A va en « a » A !’ 4d 1h!’ « a » Si le point B va en « b » B !’ 4d 1h!’ « b » Les deux points ont le même déplacement. AB = ab |
|
|
On dit que : [ab] est …………………………..
à [AB] [ab] est
« ………………………..» de [AB]
par la translation !’ 4d 1h!’ |
|
3°) Compléter la phrase :
|
Le triangle abc est ………………… du triangle ABC par la translation !’ 4d 2b!’ Ces 2 triangles sont |
|
4°) Sur du
papier quadrillé , marquer les points A , M , N puis tracer les deux segments [AM]
et [AN].
|
a) Effectuer pour le point A , un déplacement
de 3g et de 2 h ; on obtient le point « a » b) Effectuer le même déplacement ( 3g ; 2h) pour le point M puis pour le point N , on obtient les
points « m » et « n » |
|
|
|
Joindre « am »
et « an » Observer les segments [AM] et [am] ; comparer
leur longueur
et leur direction ; Faire de même avec les
segments [AN] et [an]. |
||
|
|
|
|
5°) Sur papier quadrillé , placer
les points M , N , P , S ; les joindre pour former un carré.
|
Effectuer pour chacun des 4 sommets le
déplacement ( 5d ;1b). Joindre les 4 points m ,
n, p, s , obtenus . Comparer la figure mnps
au carré MNPS |
|
|
|
|
6° ) Sur un papier
quadrillé , reporter les points :
A ( 6 ;5) ; B
( 7 ;3 ) ;C ( 6 ; 1) ;D ( 5 ;
3 )
|
a) Trouver
la nature du quadrilatère ABCD b) Effectuer pour chacun des 4 sommets le
déplacement (4g ; 1h) et trouver les codes des points « a » , « b » , « c » , « d »
obtenus. |
|
|
Tracer les segments : [Aa] ;
[B b ] ; [ C c ] ; [ D d ] ; comparer les longueurs et les directions de
ces 4 segments |
|
|
|
|
|
7°)Sur un papier
quadrillé , reproduire la figure F1. a) Effectuer tous les points de cette figure la
translation de code ( 3d , 1h) puis tracer la figure
F2 obtenue . |
|
|
Effectuer maintenant ,
pour tous les points de cette nouvelle
figure , le déplacement ( 3d ; 2b) et tracer la figure F3 obtenue . Donner le code de déplacement qui permet
d’obtenir directement la figure F3 à partir de la figure F2 . |
|
|
|
|