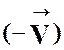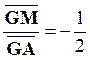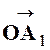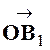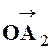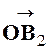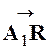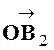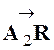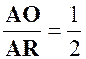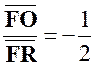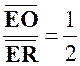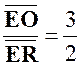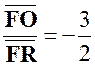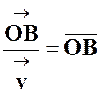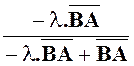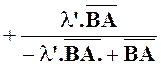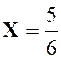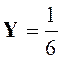Somme géométrique : « contour polygonal » ; « résultante » ; « propriétés »

 Somme de deux vecteurs.

 22   Exemples d’  applications :

Voir :  pb n° 11    ( la droite d’ Euler)   ; suite(   d’une application du théorème sur la droite d’Euler)

On sait que la somme géométrique de plusieurs vecteurs quelconques est définie au moyen de la construction suivante, basée sur l’emploi des vecteurs équipollents, c'est-à-dire des vecteurs dont les supports sont parallèles et qui ont même grandeur et même sens.

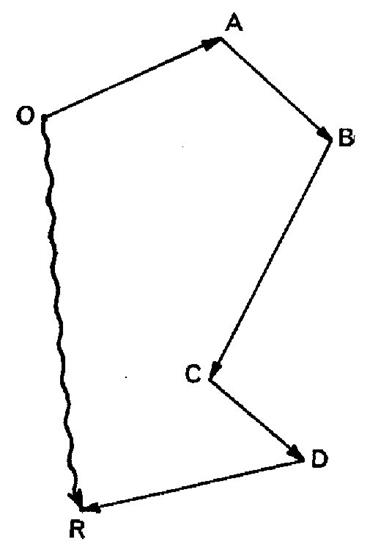
Exemple :

Par un point « O »de l’espace on même un vecteur   équipollent  à l’un des vecteurs donnés , par « A » les vecteur   équipollent à un autre des vecteurs donnés et ainsi de suite…

On forme ainsi une ligne brisée dont les côtés sont des vecteurs tels que l’origine de chacun d’eux coïncide avec l’extrémité du précédent . (les vecteurs sont placés bout à bout).

Cette ligne brisée s’appelle un « contour polygonal ».

Le vecteur qui a pour origine et extrémité celles du contour s’appelle « résultante » du contour polygone ou « somme géométrique » des vecteurs proposés :

Ainsi :     (relation1)

Si on change le point de départ « O » , le vecteur   est remplacé par un vecteur équipollent.

Notez que dans la relation 1  ( égalité)  les signes + sont les symboles d’une construction à effectuer.

Si le contour (polygone des vecteurs) se ferme , la somme géométrique est dite « nulle » ?

On écrit            ou 

Le symbole   se lit : « vecteur zéro ».

On appelle « vecteur zéro », tout vecteur dont l’origine coïncide avec l’extrémité.

On sait que la somme géométrique est commutative et associative. 

Info :

La multiplication par un scalaire est également distributive par rapport à l’addition géométrique.

Ainsi :   =    

Et en sens inverse :    =

La somme géométrique est commutative.

     =        

La somme géométrique est associative.

   =   + =   + 

Les propriétés

  =   +               associativité

  +    =    +     = 

  +    =   + = 

permettent de dire que les vecteurs étudiés ici possèdent la « structure de groupe relativement à l’addition »

La notation  désigne le vecteur  de  en permutant l’origine et l’extrémité . Par exemple :    c’est : 

Info :+

Somme de deux vecteurs :

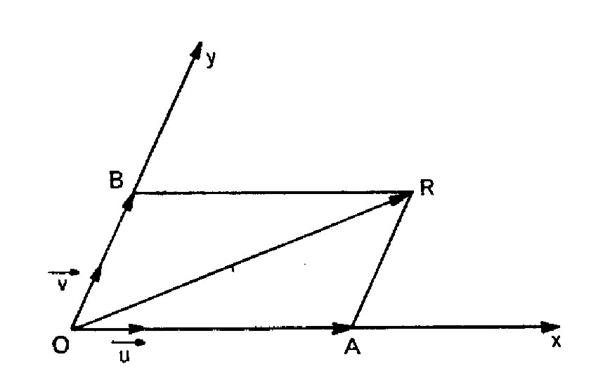
Dans le cas de deux vecteurs la somme géométrique est la diagonale du parallélogramme construit sur ces deux vecteurs ramenés à la même origine. 

  =    +     ( relation 2)

comme les diagonales se coupent en leurs milieux « I » , on a :

  =  2    ( relation 3)

D’où l’égalité très importante :

 +    =  2    ( relation 4)

Exemples d’  applications :

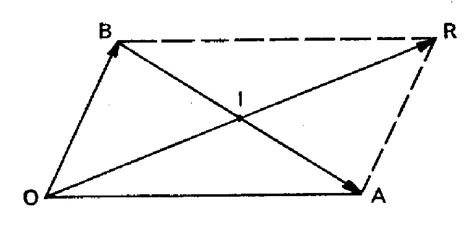
PB 1 : On divise le côté « BC » d’un triangle « ABC » en quatre parties égales par les points successifs : « M ₁ » ; « I »  ; « M ₂ »  ,   « I » étant le milieu de « BC ». Préciser la somme géométrique :

  =    +  + + +

Solution :

On note que « I » est à la fois le milieu de « BC » et de « M₁ M₂ ».

En utilisant la commutativité et l’associativité , nous écrivons :

  =   ( + ) +  (  + )  +

Nous appliquons alors les remarques de la relation 4 .

( + ) =  2    ;   et ;  (  + )  = 2

Nous avons donc :

  =   2  +  2  + =   5

Pour construire  , joindre  « AI » et quadrupler cette largeur à partir de « I ».

Voir la solution  en statique  graphique ……..

PB 2 : On divise le côté « BC » d’un triangle « ABC » en cinq  parties égales par les points successifs : « M ₁ » ; « M₃ »  ; « M ₂ » ; »M₄ » ,   «se succédant dans cet ordre à partir de « B ». Préciser la somme géométrique :

  =    +  +  + +   +

Début de solution :

1°) Ecrire :   =   (+  ) +  ( +   ) + ( + )

2°) introduire le milieu  « I »  de « BC » et appliquer  la relation 4

  =   2  +  2  +2  =   6

Voir la solution  en statique  graphique avec  6 vecteurs forces.…

PB 3 : généraliser les deux questions  ci- dessus  en divisant le côté « BC » en  « n » parties égales . Il y aura lieu de distinguer deux cas de figure selon que « n » est pair  ou impair.

Parfois la solution résulte de l’introduction d’un point arbitraire « O ».

Pb 4 : On considère quatre points  « A,B,C,D » non situés tous les quatre dans un même plan. Evaluer la somme géométrique.

  =  +   +   +

Solution : Introduisons un point « O » arbitrairement et écrivons :

  =  +       ;   =   +   ;   =   +   ;    =  +

Il deviendra :

  = +   +  +   +  +   +  +

Nous opérons un regroupement de termes ( application des propriétés : commutativité et associativité)

  =(  +  )  +  ( + )+ ( +   ) +  (  +  )             ; rappel (  +  )  =  et ainsi de suite !!!

  = + ++

  =

remarque : En permettant « CD » et « BC » on a tout de suite :

(   +   )+  (    + )   =     +    =  

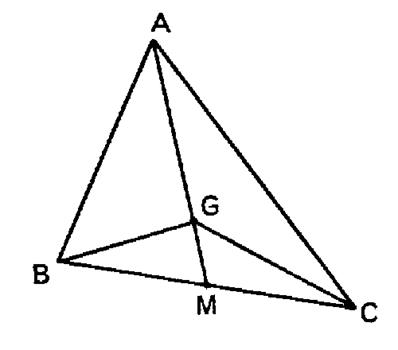
Pb 5 : Etant donné un triangle « ABC » , déterminer le point « G » de ce triangle , tel que :

  +   +    =                      ( 1 )

Solution : 

Désignons par « M » le milieu de « BC ». D’après le relation 4 :    +    =  2                    ( 2 )

Et la relation  de l’énoncé  devient :    +2  =           ( 3 )

(D’après ce que nous avons vu dans le division harmonique ) Cette relation montre que les trois points   AGM   sont alignés  et que : 

Le point « G » est situé sur la médiane « AM » , au tiers de celle –ci à partir du côté « BC »

Si on avait introduit le milieu  « N » de « AC »  ou le milieu « P » de « AB » on aurait  eu :

+ 2  =  

ou

  +  2 =  

et on en conclut que les trois médianes d’un triangle sont concourantes.

PB 6 :   Soit « M » et « N »  les milieux respectifs des côtés « AB »  et « AC » d’un triangle « ABC » . Démontrez  que « MN » est parallèle à « BC » et égal à  .

Solution :

Ecrire :   =   +    =   2  + 2   =   2 

Pb7 :  Etant donné quatre points de l’espace «  A , B , C , D » non coplanaires ( non situés tous les quatre dans un même plan).

Démontrer que l’on peut trouver un point « G » tel que :   +   +   +    =       (généralisation du pb. 5 )

On aura avantage à introduire le point « g » tel que :

+  +  =  

Cours :    Les propriétés de la somme géométrique apparaissent comme un outil de premier plan pour donner des démonstrations…..

Voir à la suite d’autres exemples.

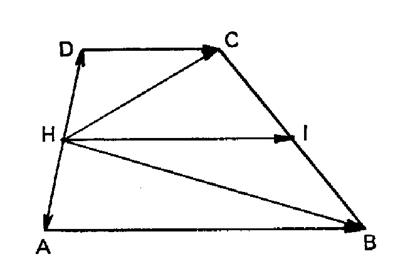
Pb 8 : Démontrer que le segment de droite qui joint les milieux des côtés non parallèles d’un trapèze (non croisé) est parallèles aux bases et égal à leur demi- somme.

Solution :  « I » étant le milieu de « BC » et « H » celui de « AD » :

 +   =      ( 1 )      (voir info )

Mais :

 =    +               ( 2 )

et

 =    +          ( 3 )

En substituant dans  ( 1 ) :

 +     +  +   =  2                        ( 4 )

ou 

 +  +   +   =  2

et comme « H » est le milieu de « AD » , la première parenthèse est nulle. Il reste :    +   =  2      ( 5 )

qui , eu égard au parallélisme de « AB » et « CD » , établit  la propriété.

Pb 9 : On considère quatre points «  A B C D » non situés dans un même plan ( tétraèdre )  

Démontrer que les segments de droites définis par les milieux  de « AB » et « CD » ;  de « AC » et « BD » ; de « AD » et « BC », sont concourantes en un points « G » qui est le milieu de chacun d’eux.  ( faire la figure)

Indications : « M » milieu de « BC » ; « N » milieu de « CD » ; « P » milieu de « DB » ; « Q » de « AD » ; « R » de « AC » ; « S » de  « AB ». 

Solution :

1°) Introduire le point « G »  tel que :   +   +   +    =    ( voir pb. 7 )

2°)   +   =      ;   +    =   d’où :  =

« G » est milieu de « SN »

3°) les autres regroupements   +   ;  +      montrent que « G » est le milieu de « QP » . De même pour le troisième segment.

Pb 10 : Soit un trapèze «  A M M’ A’ » dont les bases sont « AA’ »  et « M M’ » . On considère  les points « G » de « AM » et « G’ » de « A’M’ » tels que :

 +  2  = 0 ;    +  2 

1°) Montrer que « GG’ » est parallèle à « AA’ » .

Soit un triangle « ABC » situé d’un même côté d’un plan « P »

Soit « G » le point de concours des médianes . On projette les points « ABCG »  sur le plan « P » en «  A’B’C’G’ »

Démontrer :   3 GG’ =  AA’  + B B’ + C C’

Nous terminons ces exemples par un problème proposé à une épreuve de niveau 4 .

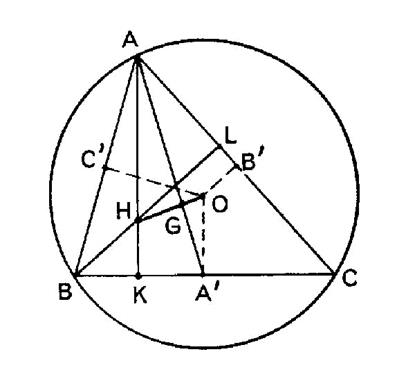
Pb 11 : On considère un triangle « ABC »    ( pré requis : le tracé du cercle et de la droite d’Euler)

1°) « G » étant le centre de gravité du triangle, démontrer que :   +   +   = 0

« M » étant un point quelconque du plan ,démontrer que :   +  +  =  3

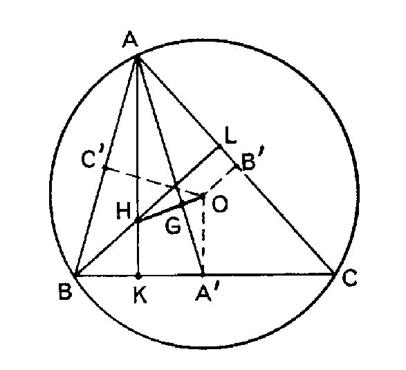
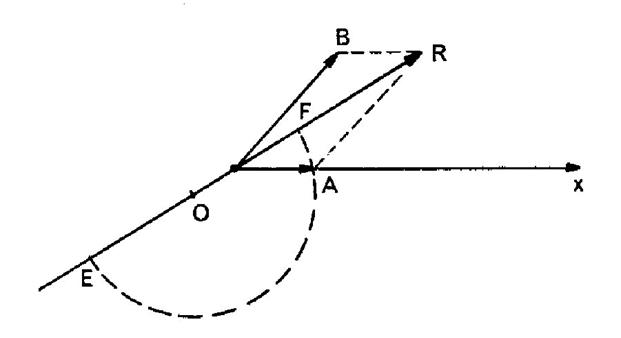
2°)  « O » et « H » étant respectivement le centre du cercle circonscrit et l’orthocentre du triangle,  ( voir figure ci contre)

Démontrer que :

  =   + +

En déduire que si «  A’ B’ C’ » sont les projections de « O » sur « BC » , « CA », « AB ».

On a    =  2     ;   =  2    ;  = 2

En déduire la valeur de la somme géométrique :

 +   + +   + +

Cette somme peut-elle être nulle ?

3°) Déduire des « 1° » et   « 2° » que les points « OHG » sont alignés et indiquer leurs positions respectives sur la droite qui les joint.  ( devoir niveau 4)

Solution :

Certains points ont été déjà envisagés dans ce qui précède . Nous reprenons cependant une solution d’ensemble :

1°) « M » étant le milieu du côté « BC » ; on écrira :   +    = 2  et la somme géométrique à évaluer sera :

2   +  

Elle est nulle puisque « G » est le point de concours des médianes du triangle.

En outre , « M » étant un point quelconque du point.

 +  +  =    +    +  + +  +

                                     = +    +  +     ; puisque    +   +   = 0

 +  +   =    3  

Projetons la somme géométrique :

 =    + +    (1)  sur le côté « BC »

les vecteurs  et   étant symétriques   par  rapport à la médiatrice « OA’ » de « BC » , ont les projections dont les mesures algébriques se détruisent.

Il ne reste que la projection de   qui est .

L’extrémité de  appartient donc à la hauteur « A’K » . On montrerait de même en projetant     sur « AC » que l’extrémité  de  appartient à la hauteur « BL » . Donc l’extrémité de  est  l’orthocentre du triangle et l’on a :

  =   + +    ( 2 )

Mais  « A’ » étant le milieu de « BC » : +  =   2     ( 3 )

Et la relation (2) s’écrit :  +  =   + 2 

2   =                  ( 4 )

On verrait de même que :

2   =       ( 5 )     ;   2   =    ( 6 )

Evaluons la somme : 

  =     +     +   +    + +                      ( 7 )

En tenant compte de ( 4 ) , ( 5 ) , ( 6 )  nous aurons :

  =  +    +  +    +   +

ou     =   (  +    +   )     ( 8 )

Appliquons la relation qui  termine ( 1°) au cas ou « M » est en « H » .

Nous aurons :  +    +    =  3

Finalement , d’après ( 8 ) et ( 9 ) :   =

Cette somme géométrique ne peut être nulle que si les points « H » et « G » coïncident , c'est-à-dire si le triangle est équilatéral..

3°) On a trouvé deux expressions  de    + +   , savoir :

 + +    =  3 

 + +    = 

On en conclut : =  3 

Les vecteurs   et   ont même support. Les points «  O , G , H »  sont alignés et  « G » est entre « O » et « H »  au tiers du segment « OH » à partir de « O ».

Ce qui donne  le  théorème :  ( droite d’ Euler   ) ……………… (application : triangle…)

Dans tout triangle , le centre du cercle circonscrit, le point de concours des médianes  ( centre de gravité) et l’orthocentre  , sont alignés ; ( droite d’Euler) .

Le centre de gravité est au tiers du segment d’Euler à partir du centre du cercle circonscrit.

Cours

On rencontre fréquemment le problème inverse, celui de la décomposition d’un vecteur donné, en deux (dans un plan) ou trois (dans l’espace)  autres vecteurs  ayant la même origine et remplissant certaines conditions imposées.

Dans le cas de la décomposition en deux vecteurs, il faut songer au fait que le vecteur donné sera la diagonale d’un parallélogramme ,ayant les vecteurs cherchés pour côtés.

Dans le cas de la décomposition en trois vecteurs on n’oubliera pas que le vecteur donné doit être la diagonale d’un parallélépipède dont trois arêtes concourantes seront les vecteurs cherchés.

Dans les exemples qui suit , commençons  en faisant intervenir que des constructions géométriques.

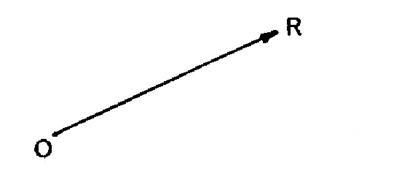
Pb 12 :

Décomposer un vecteur  donné en deux autres connaissant la longueur de l’un d’eux et le support de l’autre.

                   On donne  le vecteur  ( fig 1)  , en « O » on trace (ou on donne) l’axe « Ox »  (fig.2) , on cherche ( d’abord) 

( fig 1)

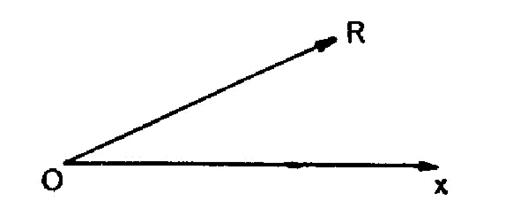
(fig.2)

Solution :Soit     le vecteur donné . Le vecteur dont on ignore la longueur  doit être porté sur « ox » . Si « A » est son extrémité , on doit avoir :

«  =    +   »

Et ,comme par hypothèse, on connaît la longueur « AR », il suffit de tracer l’arc de cercle de  centre « R » ,ayant pour rayon la longueur  donnée.

(si) Le cercle coupe « Ox » , on a deux solutions :

  ,    et   et  .

 étant équipollent à    et   équipollent à  .

Si le cercle ne coupe pas , il n’y a pas de solution.

PB 13 :  Décomposer un vecteur   en deux vecteurs de longueurs respectives  données « m » et « p ».

Début de solution : On est ramené à construire un parallélogramme dont la diagonale est « OR » et dont les côtés ont des longueurs donnés , c'est-à-dire un triangle dont les côtés mesurent « OR3 , « m » , et « p » .

Pb 14 : Décomposer un vecteur donné  en deux vecteurs rectangulaires , connaissant la somme des longueurs « m » de ces derniers.

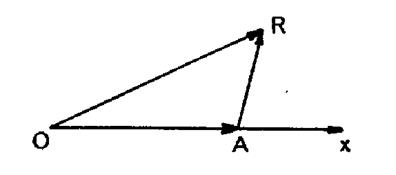
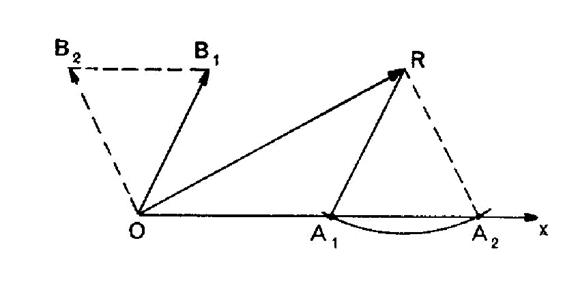
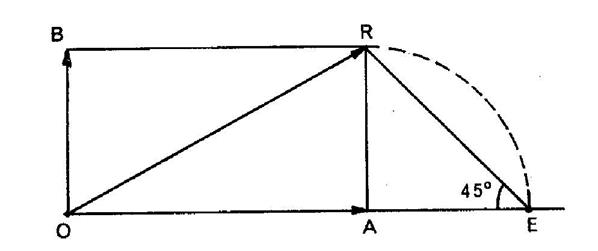
Solution :

Dans la figure d’étude ci-dessous , « AR » est perpendiculaire à « OA » et l’on connaît ; « OR » ; « OA + OB = OA + AR » .

On est ramené à construire un triangle rectangle connaissant l’hypoténuse et la somme des côtés de l’angle droit.

Si l’on rabat « AR » en « AE » sur le prolongement de « OA » , le triangle « ORE » est constructible parce que l’on connaît :

OR ; OA + AE = m ; = 45 °.

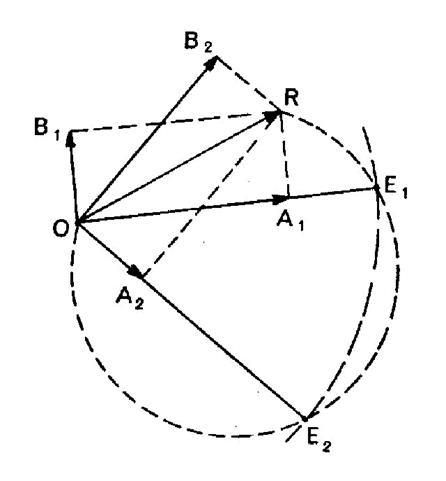
« OR » étant mis en place, on tracera l’ un des arcs  capables de « 45° » décrit sur « OR » comme corde et on coupera par le cercle de centre « O » et de rayon « m » .

On peut obtenir ainsi deux points «  E₁ »  et  «  E₂ » , donnant deux support possible par « OA » .

Le point « A₁ »  est la projection de « R »   sur  « OE₁ » ; « B₁ » s’en déduit comme quatrième sommet du rectangle «  O   A₁  R  B₁ ».

De même  pour  le point « A₂ »  est la projection de « R »   sur  « OE₂ »

Remarque : Il est possible d’utiliser le second arc capable ; on a des solutions  symétriques par rapport à 

Pb 15 :  Décomposer un vecteur donné  en deux autres , connaissant la somme des longueurs  de ces deux autres et l’angle aigu de leurs supports.

Début de solution : Suivre pas à pas la solution du problème « 14 » . On est ramené à construire un triangle connaissant un côté , la valeur de l’angle opposé et la somme des longueurs des deux autres côtés.

Pb 16 :  Décomposer un vecteur donné  en deux autres , connaissant le support du plus petit et sachant que le plus grand module est le double du plus petit.

Solution :

Si   est le vecteur de plus petit module, porté par «  Ox » ; l’autre  se retrouve en  dans le parallélogramme « OARB », et l’on a :

Le point « A » appartient au cercle d’Apollonius attaché au segment « OR » dans le rapport  (voir info : pb 1 de la division harmonique)

On prendra donc les conjugués harmoniques de « O » et « R » tels que :

   et   

« A » est le support « Ox » et sur le cercle de diamètre « EF »

« B » s’en déduit en prenant   équipollent à  

Pb 17 :  Décomposer un vecteur donné  en deux autres vecteurs , connaissant le support du plus long et le plus petit module vaut les  de celui du plus grand.

Début de solution :

L’extrémité du vecteur de plus grand module est sur le support donné « Ox » et sur le cercle de diamètre « EF » , « E » et « F » étant tels que :

   et  

Pb 18 :  Décomposer un vecteur donné  en deux autres vecteurs , connaissant le support de l’un d’eux  et le rapport « k » de leurs modules.

Cours

Etant donné deux axes  « Ox »  et « Oy »  munis de vecteurs unitaires :    et     et un vecteur    , la décomposition de ce vecteur en deux autres   et  , portés respectivement par « Ox »  et « Oy » peut  revêtir une forme toute particulièrement importante.

Pb 19 :

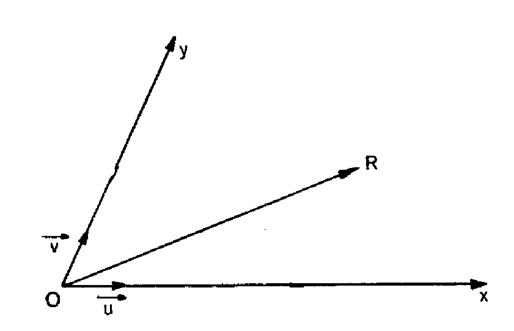
Etant donné deux axes  « Ox » et « Oy » munis de vecteurs unitaires    et     et un vecteur    du même plan , montrer qu’il existe un couple «  x , y » de nombres algébriques tels que :

   = x    +   y 

et que le couple «  x , y » est unique.

Les longueurs de   et    prises pour unités ne sont pas forcément les mêmes.

Solution :

Le vecteur   se décompose en deux vecteurs    et   portés respectivement par « Ox » et « Oy » et  l’on a :

  =     +         ( 1 )

Mais     et     sont colinéaires . Si l’on désigne par « x » la mesure algébrique  de  , c'est-à-dire :

 =    = x     ;     =  x 

( « x » peut être positif ou négatif )

Si l’on désigne par « y » la mesure algébrique  de   :

 = y         ;     =  y .

la relation (1 ) devient :   =   x .  +  y .            ( 2 )

Les nombres « x » et « y » sont uniques, car si l’on avait un autre couple «  x ‘ y ‘ »il faudrait écrire :    =   x ‘ .  +  y ‘ .     

D’où  par soustraction géométrique « membre à membre » :

( x – x ‘ )   + ( y  - y ‘ )  = 

Ceci indiquerait que les  vecteurs    et      sont colinéaires ( même support ) ; ce qui n’est pas. Donc :    x ‘ = x      et   y ‘ = y

Remarque :  le cas où  serait porté par « Oz »  ou par « Oy » ne fait pas exception. On aurait alors :

Soit     =  x  .  +  O .     

Soit     = O  .  +  y.     

Suite : pré requis

Nous avons déjà vu que les vecteurs possèdent la structure de groupe relativement à l’addition géométrique.

(1)

(  +  )  +    =    +  (   +  )  =    +    +   

 +    =   +   = 

 + ( - ) =  ( - ) +  = 

en outre    :     +    =    +  

On dit que le groupe est donc « commutatif »  , on dit aussi « abélien »

Nous avons aussi déjà vu la multiplication d’un vecteur par un scalaire et vu que :

( 2 )

k(  +  ) =  k  +  k

( h + k )  =  h  +  k

h( k .) =  ( h . k )

1 .   =

L’ensemble de ces deux listes de propriétés ( 1 ) dite loi de composition interne ( addition géométrique) , et  ( 2 ) dite loi de composition externe (multiplication par un scalaire) permet d’affirmer que les vecteurs que nous étudions ici ( vecteurs définis à une équipollence prés ) admettent la structure dite de l’espace vectoriel .

ET : la décomposition   =  x  .  +  y .    qui résulte du problème « 19 »  exprime que     et.  constituent une base.

Pb 20 :

On considère un triangle « OAB » fixe , quelconque .

On demande :

1°) Montrer qu’ à tout point « P » du plan de ce triangle on peut associer un couple de nombres « x » et « y » et un seul tel que :

  =  x .+ y .

2°) soit  lambda :  un nombre quelconque . On considère le point « P » de la droite « AB »  défini par   =    ; mettre  sous la forme :

 =  x .+ y .

« x » et « y » étant exprimés au moyen de  «  »

3°) Quelle relation faut-il imposer aux nombres «  »et  « ’  »correspondant à deux points « P » et « P’ » pour que ces points soient conjugués harmoniques par rapport à « A » et « B ». ?

(Sujet de baccalauréat , niveau 4 )

Début de solution :

Le 1°) est identique au problème 19,   et  jouant le rôle de vecteurs unitaires    et   sur « OA » et « OB ».

2°)   =  x .+ y .

  =   +    =    +    .  =   +     +    =   +  ( 1  -   )

Donc : x =   et   y =  1  -   

3°) Conjugaison harmonique :

ou :     =  

Réponses :  2  ’ =  +’

Pb 21 :  « OAB » étant un triangle quelconque , « P » un point de son plan et «  » un nombre algébrique , quel est le lieu du point « P » tel que :

 =  +  ( 1  -   ) ?         (1)

Solution indication :

Ramener ( 1 ) à la forme   =   .   en écrivant :

 +    =    (  +  )   +   ( 1  -   )

·         et  sont colinéaires.

·       Le lieu « P » est la droite « AB »

Pb 22 :  Soit deux systèmes d’axes « Ox » , « Oy » de vecteurs unitaires  et    et   « Ox ₁ » , « Oy ₁» de vecteurs unitaires et    , On suppose :

 =  3   - 2

 = - 3   + 4 

                                Soit « M »  au point du plan tel que :

 =  2   -             ( 1 )

                                 Relativement à « Ox ₁ » , « Oy ₁» on a aussi :

          =  X    + Y               ( 2 )

Calculer  « X »  et « Y »

Solution :

La comparaison de (1 ) et ( 2 )  donne :                       X    + Y     =   2   -                       ( 3 )

Tenons compte des expressions de   et      en fonction de   et    :

      X (3   - 2 )     +  Y  (- 3   + 4  )   =     2   -                ( 4 )

Egalons alors les coefficients de   et    :

   3 X – 3 Y =  2

-  2 X + 4 Y = - 1

Et il n’y a plus qu’à résoudre ce système pour avoir :

De nombreuses application de cette décomposition d’un vecteur  apparaîtront  dans le cours sur : axes de coordonnées.

TRAVAUX AUTO FORMATIFS.

CONTROLE

EVALUATION.