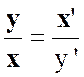Pré requis:
|
Soustraction de deux nombres relatifs |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : géométrie
plane : le bipoint |
Liste des cours
disponibles sur « les vecteurs » ; géométrie vectorielle . |
||
|
Objectif
suivant : |
DOSSIER Les VECTEURS
"colinéaires"
1° ) Reconnaître
des vecteurs colinéaires dans la
représentation graphique
2°) Condition pour que
des vecteurs soient colinéaires
|
Interdisciplinarité |
|
|
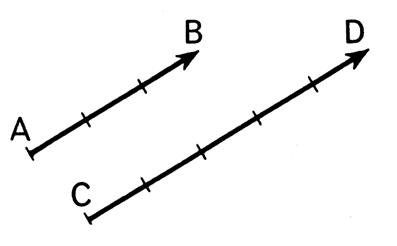
1° ) Reconnaître des
vecteurs colinéaires dans la représentation graphique : « colinéaires » signifie :" même ligne" . leur support sont parallèles ou superposés. les vecteurs ci dessous
sont colinéaires. |
||
|
|
|
|
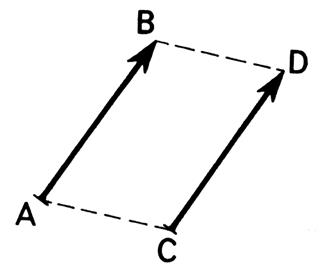
Ci-dessous les vecteurs
« colinéaires » ont la même direction
( pas forcément le même sens , la même norme .)


 Exemples :
Exemples :
![]()
|
|
soit un vecteur |
|
|
|
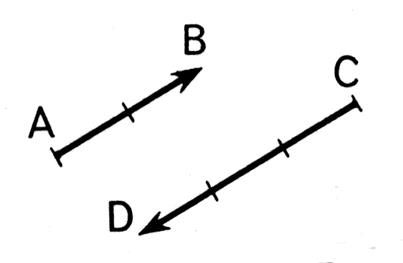
Ci-dessous : * les vecteurs ne sont pas colinéaire avec le vecteur « Les vecteurs ci dessous ne sont pas colinéaires.
Dit autrement : Des vecteurs colinéaires sont des vecteurs qui
ont des supports parallèles, (ou superposés)
indépendamment du sens et de la norme de ces vecteurs
. · Deux vecteurs sont « colinéaires » s’ils sont portés par des
droites parallèles , ou si l’un des deux est le
vecteur nul . · ( voir en rappel : multiplication d’un vecteur par un
nombre) |
|
|
|
Application : soit trois points A ,B
, C tels que
|
|
|
|
2°) Condition pour que des vecteurs
soient colinéaires
Les vecteurs
En résumé si : ( x . y ’ = x ’. y ) les
vecteurs sont colinéaires. ( nous disons que les produits en croix sont égaux ; sachant que |
|
|
|
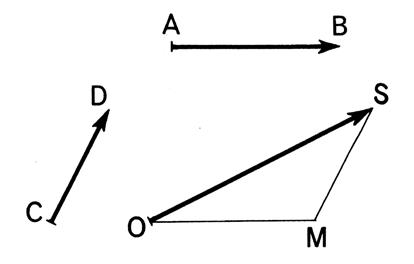
3°)
COMBINAISON LINEAIRE DE DEUX VECTEURS Soient deux vecteurs Les nombres « k » et « k ’ » sont des coefficients
de cette combinaison linéaire . ( voir somme graphique de vecteurs colinéaires) |
|
|
|
Activité : A partir des deux vecteurs |
|
|
|
|
|
|
|
4°)APPLICATION :
Calcul : Chercher le nombre « t » pour que les vecteurs Résolution :
Pour que les vecteurs soient
colinéaires il faut que : x . y’ = x’. y Avec :
x = t – 1 ; y = 3 ; x’ = t +1 ; y’ = 5 Formule : x .
y’ =
x’. y On remplace :
( t – 1) 5
= ( t + 1) 3 On développe 5t – 5 = 3t + 3 On transforme 5t – 3t = 3 + 5 On regroupe
2 t = 8 On calcule t = 4 Conclusion : Pour que les vecteurs soient
colinéaires il faut que Les coordonnées du vecteur et les coordonnées du vecteur On peut retrouver le nombre « k » tel que
il s'agit de k = |
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
CONTROLE : 1°) que signifie le mot "colinéaire"?, 2°) Quand dit - on que deux
( ou plusieurs) vecteurs
sont colinéaires ? 3°) A quoi correspond l'écriture suivante : "k |
|
|
|
1°
) Chercher le nombre « t » pour que les vecteurs 2°) Dans la représentation graphique suivantes: Dire quels sont les vecteurs colinéaires ? |
|
|
|
|
|
|
|
|
|
|
|
|
|