DOSSIER  :    Le   BIPOINT et le vecteur.

1. Définition du « bipoint » :    ( bi = deux)

2°  Notations  à connaître  :

3°)  Définition de  DROITE « SUPPORT » et  « vecteur » .

4°)  bipoint NUL.

5° ) Bipoint  confondus .  

6°) Bipoints Consécutifs.

7° ) Activité .

COURS

1. Définition du « bipoint » :    ( bi = deux)

Un bipoint « O » et « E »  est un couple   de points ordonnés.

 Il est   noté :     ( O , E  )

                                                             On écrit dans l’ordre de gauche à droite : une parenthèse ouverte  ,une lettre majuscule  « O »    pour origine , une virgule, une lettre majuscule (E pour extrémité) , une parenthèse fermée.

2°° Notations  à connaître  et à ne pas confondre :

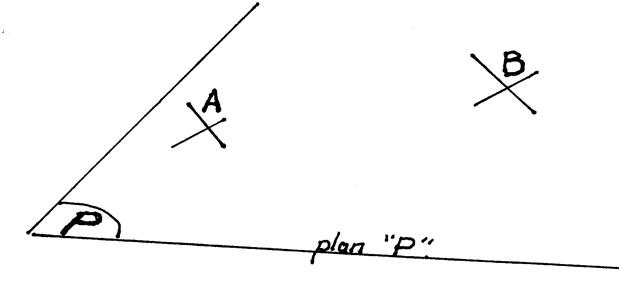
Explication :

On place deux points dans un plan :       « A » et « B »  sont deux points du plan (P) que l’on associe dans un ordre choisi d’avance. 

 Dans un bipoint , il faut une « origine »  (désignée par la première lettre écrite) et une « extrémité » (désignée par la deuxième lettre écrite) 

Remarque :  aucun trait ne lie  ces deux points.

Exemple :      Le couple de points A  et   B est appelé BIPOINT du plan (P).

( 1 )    On note le bipoint de « A » à « B »     :   ( A , B )

        où     « A » est l'origine du bipoint (A,B).  et    « B » est l ‘extrémité du bipoint (A,B).

( 2)       Si je lis  le point « B » et ensuite le point « A » dans cet l’ordre  alors  je suis en présence du bipoint  B A   ., j’écrirai : ( B , A ). 

alors « B » est l'origine du bipoint (B , A ).  et    « A »   est l ‘extrémité du bipoint (B , A ).

Remarques :     Le choix du sens de lecture est très important !!!!!!

Dans le cas  (1)    je vais de « A » vers « B » ; dans le cas (2)  je vais de « B » vers « A »

En conclusion 

Un bipoint « O » et « E »  est un couple   de points ordonnés.

 Il est   noté :     ( O , E  )

                                                             On écrit dans l’ordre de gauche à droite : une parenthèse ouverte  ,une lettre majuscule  « O »    pour origine , une virgule, une lettre majuscule (E pour extrémité) , une parenthèse fermée.

On retiendra :

donc :              Un bipoint est un couple de points orientés

(A,B) : lire «  bipoint  d’origine A et d’extrémité B »

(remarquez qu ‘une virgule sépare les deux lettres majuscules)

  Attention :

L'ordre dans lequel on écrit les deux points est important !

Le bipoint (A , B) est différent du bipoint (B, A).

(B , A) : lire « bipoint d’origine B et d’extrémité A »

Si    par un point A du plan (P) on peut faire passer une infinité de droites contenues dans le plan (P).   Par deux points distincts A et B on ne  peut faire passer  qu ‘une seule droite du plan (P).

cette droite se note ( AB) :     remarquer que rien ne sépare les lettres majuscules)

3°)  Définition de  DROITE « SUPPORT » et vecteur :

    La droite (AB)  qui passe par le bipoint AB  s'appelle SUPPORT du bipoint (A,B).

On retiendra que :   La droite passant par un bipoint s’appelle : droite « support ».

Cette droite n’appartient pas au bipoint ; elle matérialise le plus cours trajet pour aller d’un point à l’autre. !!

Remarques:

  4°)  bipoint NUL.

   On appelle « bipoint nul » si les deux points sont confondus ou superposés ;

Exemple :       si    « A » et « A' »  sont confondus ( c’est à dire : A = A' ),alors le bipoint (A,A') est appelé bipoint NUL.

  5° ) Bipoint  confondus :  

  .Les bipoints (A, B) et (A',B') sont égaux si A = A' et B = B'     ce qui signifie que

           *A et A' confondus  et    B et B' confondus

  on remarque que :

                            .Le milieu du bipoint (A,B) est le milieu du segment  AB . 

6°) Bipoints Consécutifs:

      Définition :  Des bipoints  sont dits " consécutifs" si l' extrémité de l'un est confondu avec l'origine de l'autre

 Les bipoints  (A, B) et (B,C ) sont appelés  bipoints consécutifs

7° ) Activité :

Soit :

 M,N,O,P, sont 4 points du plan  P.

n 1 °  ) Combien y a t - il de supports distincts?

n 2 °  ) Pour 2 points donnés : Combien y a t - il de bipoints par support ?   

       3°) Ecrire tous les bipoints formés par ces 4 points.      

       4°) -  Placer le point O' pour que (O,O')soit nul.

       M

      +                             O           

                                  +

         +

       P                      +N        

Corrigé de l’activité :     Réponses :

Il y a six supports distincts ; il y a deux bipoints pour  deux points donnés.

Les bipoints sont :  (M,O ) ; ( O ,M) ; (O ,N ) ; ( N , O) ; ( N , P ) ; ( P ,N ) ; ( P , M) ; ( M , P ) ;  ( M , N ) ; ( N , M ) ; ( P ,O ) ; ( O , P )

TRAVAUX  FORMATIFS  « BIPOINT »    :

  CONTROLE:

 A )  Pré requis :traduire : (  C D )   ;   [  C  D ]    ; (  C , D )

B) Répondre aux questions suivantes :

1°)Donner la définition d'un bipoint.

2°)Donner la représentation mathématique « symbolique » d'un bipoint .

3°)Que signifie (A,B) ?

4°)Que représente (dans les cases se trouvent des lettres majuscules):

     (, )

5°)Donner la représentation graphique d'un bipoint.

6°)Qu'est ce qui est important dans la représentation ,symbolique (écriture) d'un bipoint.

7°)" (AB) ";traduire en langage littérale .

8°)Quel nom donne t - on à la droite passant par  le point "A" et "B"?

9°)Si dans un bipoint ,les deux points sont confondus ,que faut-il conclure?

10°)Deux bipoints sont égaux si ......

11°)A quoi est égal le milieu d'un bipoint?

12°-)Traduire en langage littéral:  (A,C)

13°)Traduire en langage littéral:    (A,B) = (C,D);quelle conclusion peut-on en tirer?

TRAVAUX  FORMATIFS :    EVALUATION:

I)Soit deux points situés dans un plan :

                   +  E

      + D

 Nommer tous les bipoints.

II)Soit quatre points du plan  (P)

        +  C

                               + D       

   F +                  G  +         

   a)Ecrire tous les bipoints formés par ces 4 points.

   b)Combien y - a -t- il de supports distincts?

   c)Sur le plan  « P » ,  Placer le point « F » et  le point « F‘ » pour que  (F,F’ ) soit nul .