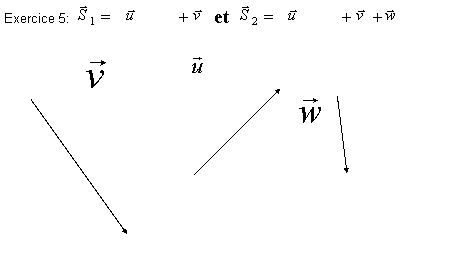Pré requis:
ENVIRONNEMENT
du dossier:
|
Objectif précédent : |
Tableau
2°)
Vecteur : présentation des objectifs. |
DOSSIER LA SOMME GRAPHIQUE DE
VECTEURS "colinéaires"
|
|
Interdisciplinarité |
|
Définitions :
« colinéaires » :
par définition Les vecteurs « colinéaires » ont la même
direction (elles peuvent être parallèles
ou confondues , mais pas forcément le même sens ,et ou ,pas forcément la même norme ) .
« coplanaires »
des vecteurs coplanaires sont des vecteurs
dont leur direction (droite support) se trouve dans un même plan. ( ces
droites peuvent être parallèles ou
sécantes)
:
COURS
1°) LA SOMME
GRAPHIQUE de deux VECTEURS « colinéaires »:
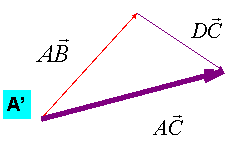
Construction de la somme : 
= 
+ 
La
somme 
de deux vecteurs
et 
. Ayant pour représentants respectifs les bipoints ( A , B
) et
( D , C ) ; ce vecteur
« somme » a pour représentant le bipoint ( A , C )
Nous pouvons écrire sous forme mathématique :
traduction :
la relation 
= 
+ 
appliqué au "cas" 
= 
+ 
CAS
GENERAL : (vecteurs
non colinéaires et , ou , colinéaires)
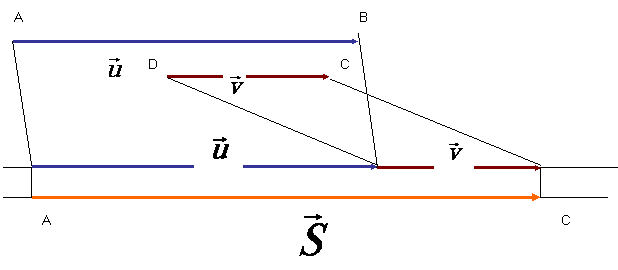
Représentation
graphique du vecteur
« somme » ; nommé :
procédure :
- fixer (sur le plan feuille ) la position du
premier point (A’)origine du premier
bipoint.
-
tracer le vecteur AB ; (( A’,B’ )bipoint équipollent AB) , on peut
dire « faire glisser par translation le vecteur AB en A’ »
- translater
le vecteur DC , (L’extrémité du premier vecteur coïncide avec l ‘origine du deuxième vecteur)
- Joindre
l’origine du premier vecteur avec l
extrémité du second vecteur ;
n
le vecteur « somme » à pour origine l’origine du premier vecteur et pour
extrémité , l’extrémité du second vecteur.
Remarques :
- le vecteur
ne dépend pas
du point « A » choisi pour
origine :
D' après
la relation de CHASLES
nous pouvons écrire que
B'
C'
A’C’
= A’B’ + B’C’ ;
A'
(A’,C’ ) est aussi un représentant de
La
construction de la somme est toujours possible.
NORME du
vecteur somme :
1°
Cas : les vecteurs ne sont pas colinéaires:
La norme du vecteur "somme" est différente
de la somme des normes des deux vecteurs :
ce qui se traduit en écriture mathématique :
II
II # II 
II + II 
II
2° Cas : les vecteurs sont colinéaires
Voir dans les exercices suivants
IIII = II 
II + II 
II
Somme
graphique de deux (ou plusieurs) vecteurs colinéaires
« colinéaires » : par
définition Les vecteurs « colinéaires » ont la même direction ( mais pas forcément le même sens ,et ou ,pas
forcément la même norme ) .
exemples
soit un vecteur ; les autres vecteurs représentent : k (leur norme sont différentes, peut-être même leur
sens ; (« k »est un nombre qui
varie .)
le vecteur « » n’est
pas colinéaire aux autres vecteurs.
Dit
autrement : Des
vecteurs colinéaires sont des vecteurs qui ont des supports parallèles, (ou
superposés) indépendamment du sens et de
la norme de ces vecteurs .
ACTIVITES :
Tracer
un représentant de la somme 
des vecteurs II 
II + II 
II
Q% dans les
cas suivants :
tracer IIII = II II + II II
Somme de deux vecteurs
colinéaires « opposés »
La somme de deux vecteurs
colinéaires de même norme mais de sens
contraire est le vecteur 
.
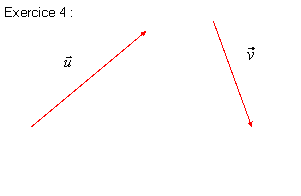
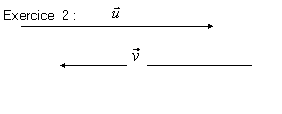
Exercice 3 :
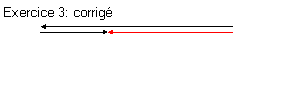
L’OPPOSE du vecteur
Activité :
tracer le bipoint ( A, B) représentant
de puis le bipoint
(B,C) représentant de
’ . La somme
+ ’ est représentée par le bipoint ( A , C ) .
Que peut -
on dire des points A et
C ?.........................................du bipoint ( A ,C )...............
Quelque
soit le vecteur du plan
« P » ,il existe un
vecteur ’ du plan « P » tel que
+ ’ = ’ + = 
TRAVAUX AUTO _ FORMATIFS
PREPARATION du devoir formatif:
1°) Traduire en langage littéral : = +
2°) Traduire en langage littéral :
IIII # II II + II II
(faire les exercices page :
............)
3°) Il est un cas ou IIII = II II + II II
donner sa représentation
graphique ; citer les deux conditions
nécessaires.
4° ) Donner la procédure
permettant de tracer la somme de
deux vecteurs (dispersés dans un plan )
5°) Quels sont les caractéristiques
du vecteur somme ( noté : ). ?
6°) Quels
sont les trois principales propriétés de
la somme de deux vecteurs (ou trois vecteurs) ?
(donner
pour chaque le modèle mathématique )
7 ° )
Quelles sont les caractéristiques du
« vecteur opposé » à un vecteur donné ? (donner un exemple
graphique)
8°) Quand
dit - on que deux ( ou
plusieurs) vecteurs sont
colinéaires ?
tracer = +
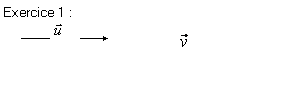
Exercice 3 :
