Pré requis:

Translations
Droite

Environnement du dossier

Index : warmaths

Objectif précédent   « Direction »

projection orthogonale d'un point .

Objectif suivant : les projections « généralités »

 

DOSSIER            "DIRECTION et sa position par rapport à une droite "

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

Objectif :  savoir définir une DIRECTION  et utiliser cette  direction pour effectuer le projeté d'un point  sur une droite .

 

A  )  « direction » :le nom donné à la « direction » s’appelle  « delta » ; symbole : d

 

 

a)     une  direction est  une droite donnée   servant de droite "référence" , elle occupe une position  géométrique  donnée dans le plan  ( par exemple : parallèle ou oblique à 45 ° par rapport au bord de la feuille )  , souvent   elle est pensée  , on peut dire que c'est une droite « virtuelle » :

 

 

                                               d₁ ;  d_2 ; d_{3   ;}  sont des directions distinctes

 

 

						d 3

 

 

 

 

 

 

 

 

 

 

( par exemple    d₃     est  "perpendiculaire au    bord  gauche de la feuille" , on peut dire aussi  que  d₃      est  "parallèle au bord inférieur de la feuille" )

 

B) Position de la direction par rapport à une droite :

 

 Cette direction peut être   sécante     à une droite   ou parallèle

 

1 ° ) cas où « d » est // à la droite « d » (ce cas n’a pas beaucoup d’intérêt )

 

 

Direction :d

 

 

		Droite : d

 

 

 

 

 

 

2 ° )  cas où « d » est sécant  à la droite « d » :

	d

 

 

 

 

a ) cas général : l’angle  a est quelconque

 

 

 

 

 

 

 

 

 

 

 

 

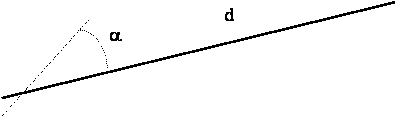
important si la direction coupe deux droites sécantes nous obtenons la figure ci dessous :

 

D1

Deux droites sécantes      D₁ D₂     et une direction d

 

 

 

	d

 

 

On peut tracer des //

 

a « d »

(les angles sont égaux)

	D2

 

 

 

 

Cette figure sera utilisée avec Thalès  et les triangles  semblables et  homothétiques

 

 

b ) CAS PARTICULIER

 

    la direction est perpendiculaire  à une droite 

 

 

@ Cette approche est importante pour mettre en relation   les repères orthogonaux  et les projections d’un point en vue de recherche de ses coordonnées)

 

 

 

 

	d

 

 

 

     d   et  d  forme un

(angle droit)

 

 

 

 

 

 

Plaçons nous dans le cas où la  direction coupe deux droites  sécantes : 

 

 

 

 

 

 

 

 

 

 

 

 

 

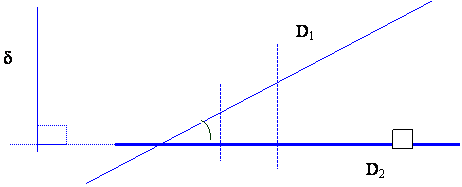
     nous obtenons une « série » de triangles rectangles  ayant un même angle

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

1 °) Qu’appelle - t- on « direction » ?

 

EVALUATION

2°) Construire  une direction et une droite :

 

a)   formant un angle de : 35°  

b)    72° 

c)     90°

 

3°) Construire  une direction et une droite D  ;

 

a)   formant un angle de : 35°  

b)    72° 

c)     90°

pour chaque cas   tracer  3 droites coupant  D  // à la direction .

 

 

4°) Construire  une direction et une droite D (horizontale) ;

 

a)   formant un angle de : 35°  

b)    72° 

c)     90°

Pour chaque figure

d)  tracer  3 droites coupant  D  // à la direction.

 

e) Terminer la figure en traçant une deuxièmeD₂  sécante à D ; (angle = 25°)