La trigonométrie : activités préalables.

NOTION
TRIGONOMETRIE : activités préalables
	Retour liste des cours de « trigo »
ACTIVITE n°1 :
I ) tracer un triangle rectangle dont la longueur de l’hypoténuse est égale à 100 mm. Relevez la valeur des 3 angles avec le rapporteur. Angle droit = ; petit angle = ; angle moyen = On nommera le petit angle : « alpha » symbole « a » On nommera le moyen angle : « bêta » symbole « b » Nommez l’hypoténuse « c. » ; le petit coté « a » ; le coté moyen « b » a) Sur le dessin relevez la longueur du plus petit côté « a » : calcul : Divisez la longueur de ce petit coté par la longueur de l’hypoténuse . ( a : c » ) Vous trouvez un nombre inférieur à zéro , ce nombre porte le nom de « sinus » . Remarque : Si le « petit angle : a » varie la valeur de ce sinus varie. On dira que le calcul de la longueur du petit coté sur la longueur de l’hypoténuse est appelé : sinus alpha que l’on notera : sin a ; à partir de cette valeur on peut trouver la valeur de l’ angle alpha en degré soit avec la calculatrice , soit avec la table des nombres trigonométriques .
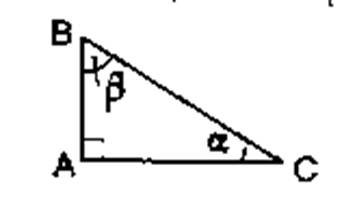
:Désignation des cotés et des angles
AB = a BC = c AC = b L’angle A (noté ) = 90 ° ( ou 100 grades) La somme des deux autres angles = 90° (on dit que ces deux angles sont complémentaires). Un des angles se nomme « angle Bêta » ( noté ) Le second angle se nomme « angle alpha » ( noté ) La somme de + = 90°
ACTIVITE n°2
Prendre une table de nombres trigonométriques ainsi qu’une calculatrice scientifique : nous allons comparer les résultats !
Voir : « tracé d’un triangle »		Pour en savoir plus : cliquez ici
ACTIVITE n°3
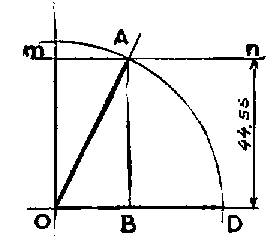
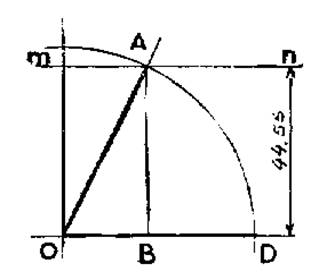
Tracé un angle à partir de la valeur de son cosinus : OA = 100 Cosinus. « » = 0,4456 on sait on en déduit que la longueur de AB : AB = 100 fois 0,4456 AB = 44,56 Remarque : le tracé sera approximatif On retiendra que : le « sinus » est égal à la mesure de OB !

ACTIVITE N° 4 : Construction et mesure d’un angle :
Savoir construire ( tracer ) un angle de 35,5° ( on exploitera ce que l’on sait sur le cosinus )	Pré requis :cliquez ici
Rappel : Lorsque l’on a un triangle rectangle tracé , pour trouver la valeur décimale d’un cosinus , il suffit - de mesurer la longueur de l’hypoténuse et la longueur du côté adjacent - , et de faire le rapport de la longueur du côté adjacent par la longueur de l’hypoténuse. On peut tracer un angle dont on connaît la valeur en degré L ici on donne l’angle = 35,5°) 1°) On recherche la valeur décimale du cosinus de 35,5° , avec la table ou la calculatrice . 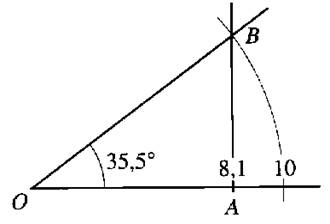on lit sur la table que cosinus de 35,5° est sensiblement égal à 0,81 ( » 0,81 ) soit = (SOS rappel) 2°) Procédure de tracé : - tracer un arc de rayon 10 cm ; - sur [ 0x) placer le point « A » tel que OA = 8,1 cm - tracer une perpendiculaire à [ 0x) passant par « A » et coupant l’arc de cercle en « B » l’angle AOB vaut 35,5° (à vérifier avec un rapporteur)
Conclusion :pour construire un angle on peut utiliser un rapport trigonométrique.
ACTIVITE N°5 : MESURE d’ un ANGLE :
Rechercher la valeur d’un angle « x O y » tracé sur un plan , sans le rapporteur .
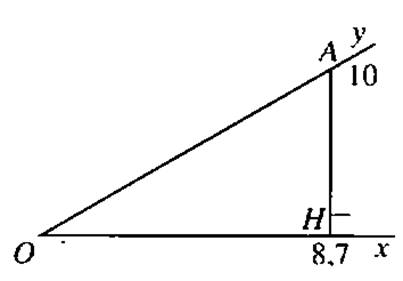
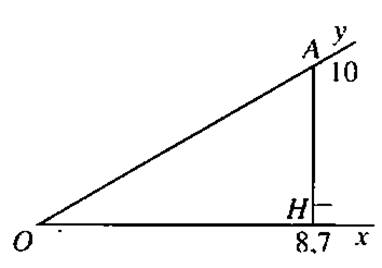
Procédure : les deux demi droites Oy et Ox étant tracées , il faut - placer un point « A » sur [Oy) tel que OA = 10 cm ; - tracer la projection orthogonale de « A » sur [Ox) (image de « A » est « H ») - mesurer la longueur « OH » ( = 8,7 cm) - on en déduit le cosinus de l’angle « xOy » = = 0,87 A l’aide de la calculatrice ou de la table : on obtient la valeur de l’angle = 29,5°

Commentaire : on trace un triangle rectangle le troisième côté étant AH , on applique la relation trigonométrique : la valeur décimale du cosinus est donnée par la calcul : ( côté adjacent / hypoténuse) ; Soit Cos « O » = lg. OH / lg. OA ; la longueur de OH est mesurée ( = 8,7 cm) Soit : Cos = 8,7 / 10 Ensuite on lit sur une table la correspondance avec la valeur en degré ; ainsi à la valeur du cosinus « 0,87 » correspond l’angle de « 29,5° » On aurait pu prendre la relation qui permet d’écrire que le sinus d’un angle est égale la longueur du côté opposé à l’angle divisé par la longueur de l’hypoténuse. Soit sin O = lg. AH / lg. OA

ACTIVITE 6 :
Construire un angle de 37 °à l’aide du cosinus .		Pré requis :cliquez ici
ACTIVITE 7
Mesurer l’ angle « xOy » donné sans le rapporteur .
-