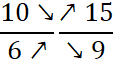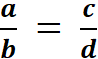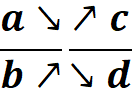|
|
|
|
|
|
|
Fractions
équivalentes (égalité de deux
fractions) |
|
L’égalité de deux
fractions |
Objectif
suivant : |
DOSSIER : PRODUIT EN CROIX et règle de trois
|
|
COURS |
|
|
Corrigé Contrôle |
|||
|
|
|
>>>> Devoir type. |
|
|
|
||
|
Partie 1 (vue au collège ) ( info sos) |
|||
|
Simplifions : Calculez : |
|||
|
On
dit parfois que |
|
||
|
|
|||
|
· Vérifiez que
· Puis
vérifiez en effectuant le produit en
croix : 8 fois 21 = 168 et 14 fois 12 = 168 |
|||
|
Ce
que vous venez de constater sur deux exemples , nous
allons le prouver dans le cas général :
On peut
écrire
Puisque En
définitive : s i |
|||
|
Inversement :
Considérons deux écritures fractionnaires Cherchons
si Puisque : En
définitive , si : |
|||
|
ON
résumera alors ces deux propriétés en un seul énoncé : |
|||
|
A
retenir : « a »,
« b » , « c » , « d » sont
des nombres et « b » et « d » sont des nombres non
nuls ; Dire
que : |
|||
|
On
peut ainsi savoir si deux écritures fractionnaires représentent la même nombre. On
vérifie l’égalité des « produits
en croix » |
|||
|
|
|
|
|
|
|
|
|
|
|
Partie
2 . |
|
|
|
IMPORTANT:
On
dit que "Deux fractions sont équivalentes si .......on peut le vérifier " ? Par
le produit en ...croix.
Procédure permettant de vérifier si deux fractions sont équivalentes:
Pour s’assurer (ou
vérifier) que deux
fractions sont équivalentes, il suffit de transformer l’égalité des deux
fractions.
1°) On transforme ce modèle mathématique:
= 
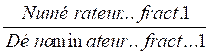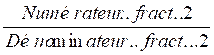
en une égalité de deux produit :
Le numérateur. de la .fract.1
« multiplié » par Dénominateur
.de la fract. 2 est égal au Numérateur de la fract.2
« multiplié » par Dénominateur de la fract
1
2°) On effectue les multiplications
|
Numérateur..fract.1 multiplié par
Dénominateur .fract. 2 |
Résultat 1 |
|
Numérateur fract.2 multiplié par Dénominateur fract 1 |
Résultat 2 |
3°) et on compare les résultats : résultat 1 = ? = Résultat 2
4°) On conclut:
(après analyse des résultats)
a) si les produits sont égaux ;les fractions sont dites équivalentes.
b) si les produits ne sont pas égaux ;les
fractions données ne sont pas égales
Exemple: On reprend
l’exercice précédent:
Enoncé :
La fraction 22 /30 est-elle équivalente à la fraction 583/795 ?
On
applique la procédure:
1°) On
énonce:
Si
est égale à 
alors 22 x
795 est égal à 583 x 30
2°) on effectue les calculs:
22
x 795 =
17 490
583
x 30 = 17 490
3°) on compare les
résultats :
Est ce que 22 x 795 est
égal à
583 x 30 . après
calcul on trouve ( 17490=17490)
4°) On tire une Conclusion suivante : les
fractions et sont équivalentes;
on peut donc
écrire que =
En
résumé:
Deux fractions (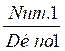
et 
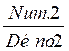) sont
équivalentes (c’est à dire) : 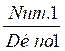= 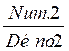si « Num.1 x
Déno.2 » = « Num.2 x Déno.1 »
Traduction en langage littérale:
Deux fractions sont équivalentes si le produit
du numérateur de la première fraction par le dénominateur de la seconde
fraction est égal au produit du numérateur de la deuxième fraction par le
dénominateur de la première fraction.
Remarques importantes:
On appelle cette méthode : le produit
en croix.
Lorsque nous aborderons
la leçon sur les proportionnalités on dira: que le produit des extrêmes est égal au produit des moyens ,
(les extrêmes étant « Num.1 » et « Déno.2 », les moyens
étant « Déno.1 » et
« Num.2 ») soit :
= 
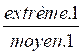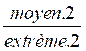si extrème.1 x
extreme.2 = moyen.1 x moyen.2
Applications :algèbre
« résoudre »
avant
de résoudre
il faut transformer l ‘égalité donnée ;en
appliquant le produit en croix
|
|
|
|
|
|
|
|
|
|
5x =12 |
7 |
7 x = 3 |
7 |
||||
|
5x = 36 |
3 x =
35 |
7 x
= 12 |
12 x = 35 |
||||
|
Pour résoudre :SOS
cours |
Pour résoudre :SOS cours |
Pour résoudre :SOS cours |
Pour résoudre :SOS cours |
||||
|
x= 36 / 5 |
x = 35
/ 3 |
x =12 / 7 |
x =35 / 12 |
3|
Utiliser pour calculer la quatrièmes proportionnelle |
Cliquer
ici |
La
règle de trois
La « règle de trois » s ’ applique à la
forme mathématique :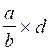 
= ? (=
c )
cette
écriture doit se transformer sous la forme
=
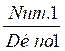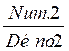
tel que : 
=
; l ‘ égalité est
vraie si : ad = bc
Nous obtenons le produit « en croix »
suivant : a 
d = c b
|
CALCULS PARTICULIERS( utile en trigonométrie ; les proportions …..) |
Domaines utilisant ce type de difficulté : le poids
, la masse , la pression , la vitesse moyenne , …. … )
Soit la forme :
« une fraction est égale à un
nombre »
(1) 
= c ; on recherche ou « a » ou
« b »
On transforme
le nombre "c" sous
forme de fraction de dénominateur égal à "1" tel que
: c = 
Alors obtenons
une égalité équivalente :
= 
|
Voir l' égalité de deux fractions |
Après
transformation de l'égalité =
Et en effectuant le produit en croix on obtient :
a 1 = c b
A partir de la même égalité = , on obtient après
transformation " b "
Ainsi 
= b ;
ce qui donne b = 
EXERCICES : d ' applications
numériques
|
|
Calcul de "x" : procédure |
|
1°)transformer
l'égalité: 2°) faire le produit en croix: 1 3°) faire le calcul : 1 4°) vérifier si 65 : 13 = à
« 5 » réponse
« oui » 5°)rendre compte : x = 65 |
|
|
13 :
x =
5 s'écrit |
1°) transformer l'égalité: 2°) faire
le produit en croix:
1 3°) faire le calcul :
5 4°) poser l'égalité 5 x = 13 5°) transformer l'égalité (on divise les deux membres par 5 ;SOS cours )
(5 x) : 5 = 13 : 5 6°) calculs : (5 x) : 5 = x 13 : 5 =
2,6 7°) rendre compte : x =
2,6 vérifier si 13 : 2,6 est =
à 5 (oui) |
|
c) |
Aucun problème
:* Faire la division 13 : 5 = 2,6 Conclure :
x =
2,6 |
x = 5 
|
|
TRAVAUX AUTO FORMATIFS. |
|
||||||||
|
|
CONTROLE: 1 ° ) Enoncer la procédure permettant
d’effectuer « le produit en croix ». EVALUATION: I) On nous donne deux fractions ; II ) CALCUL
ALGEBRIQUE : Transformer , par le produit en croix , les fractions équivalentes :
et encore : a) Interdisciplinarité |
|
réponses : a)
x = 13 5 ;
b )
13 = 7 x