|
Module :
la fraction – les rationnels |
DOSSIER : 182 - 183 |
|||
|
LOGICIEL warmaths ; Pour Aide et
Formation Individualisée
; REMEDIATION mise à /NIVEAU : niveau VI |
||||
|
TRAVAUX
NORMATIFS Matière : MATHEMATIQUES. Niveau VI et V |
||||
|
REGLE DE TROIS. |
||||
|
|
||||
|
Info 1 @ « cours sur la règle de trois.… » ; Info 2 @ « notion … » ; Info 3 @ « cours sur … » |
||||
|
EDOUART a payé 90 €
un tonnelet de En disant : j’établis
une règle de trois; Ce
calcul qui comporte une division et une multiplication est écrit avec trois
nombres. Il est pratique, parce que : 1°) on peut commencer par la multiplication, ce
qui donne parfois un résultat
plus exact que la recherche de la valeur de l’unité;
et
1,666 ..fois 24 vaut environ : ……………….. 2°) on a des calculs plus faciles si on peut simplifier
en divisant par un même
nombre la grandeur sous le trait et l’une des grandeurs du dessus
|
||||
|
TRAVAUX
CONTROLE |
||||
|
Les
questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. |
||||
|
|
||||
|
Série 1 |
||||
|
.1 -En 5 jours, un
ouvrier gagne 168 € . Quel est son gain dans un mois où il travaille 21 jours
? 2.
3.
15 cahiers coûtent 2,4 € et
pèsent |
||||
|
Série 2 |
||||
|
Que
puis-je calculer par une règle de trois ? Posez-la, effectuez-la. |
||||
|
4. 5kg de peinture, couvrent
5. Pour faire 6. Un
bidon de |
||||
|
|
||||
7. Faites les calculs indiqués, après avoir simplifié
a) par
10, 100 ou 1 000
![]()
b) par 2 ou par 5
![]()
8. Effectuez, après avoir simplifié
![]()
![]()
9. ![]()
![]()
10. Rendez
les nombres entiers avant de simplifier, puis effectuez
240
x 1,8 9,6 x 36 48 x 7,5 3,5
x 14 17 x 2,25
1,2 2,4 2,5 0,5 0,25
11. D’une
barre de fer de
Une automobile consomme
|
Quelle
est sa consommation en Je
calcule une consommation en litres. En En En
|
Quelle
est sa consommation en Je
calcule une distance en kilomètres. Avec
En Avec
|
|
Retenons 1° ) On ne peut établir de règle de trois que pour des grandeurs
proportionnelles. 2° ) Le 1er terme de cette règle est de même nature que
la réponse cherchée. |
|
11. D’une barre de fer de
12. On a payé 16,20 € un rôti
de
a) Combien
paie-t-on pour un rôti de
b) Quel est le prix du kg de rôti ? Vérifiez le résultat
précédent.
13. Un camion pèse, vide,
14. Jean-Paul a acheté 60 billes en verre pour 5 € .
a) Combien en aurait-il pour 8 € ? (on calcule un
nombre de billes).
b) Combien paierait-il un sac de 144 billes ?
(on calcule un prix).
15. Le rôti de veau que j’ai acheté coûte 8,82 € et pèse
a) Combien aurait-elle payé un rôti de
b) Quel est le poids d’un rôti de 14,70 € ?
16.
cidre donnent 24 sacs de
17. Un motocycliste roule à
a) Qu’exprime chacun des quotients suivants ,
![]()
b) Combien de
minutes faut-il à te motocycliste pour parcourir
c) Quelle distance
parcourt-il de 10 h 30 mn à 11h 15 mn ?
18. Avec
a) Quelle masse
de pain fabrique en une semaine un boulanger qui utilise 18 sacs de
farine de
b) Quelle masse
de farine a utilisé un boulanger qui a fabriqué
19. Un cultivateur vend ses pommes après l’hiver; il prévoit un déchet
de
a) Quelle
sera la masse vendable pour une
récolte de 24 q ?
b) Quelle était la masse récolté qui a permis, une vente de 2 800
€, à 1,60 € le kg ?
20. Examinez les pesées de fil de fer représentées ci-dessous
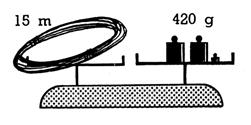
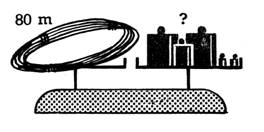
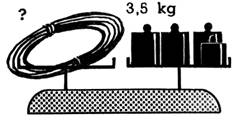
; posez les questions qui correspondent aux points
d’interrogation; répondez-y
Liste des différents cas traités de règle de
trois.:
|
|
|
|
|
|
|
|
|
|
|
|
|
|