INFORMATIONS : on
verra les différentes règles de trois
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pré requis:
|
|
|
|
Fraction
équivalente |
|
|
|
|
Objectif
précédent : 1°)La règle de trois simple et directe |
Tableau |
||
|
|
|
|
|
DOSSIER : "la
REGLE de TROIS SIMPLE et INVERSE "
|
|
COURS |
Devoir
Contrôle |
Interdisciplinarité |
|
Corrigé évaluation |
||
|
|
|
|
|
|
|
|
Notion de la
règle de Trois :
Il existe de
nombreuses relations qui se calculent uniquement au moyen de la multiplication
et de divisions successives ; ainsi ; par exemple ; j’ai acheté
15 bouteilles pour 120 € , je veux savoir combien me coûteront 40
bouteilles ; ou bien j’ai gagné 240 € en travaillant 6 jours et je veux
savoir combien on me payera en un mois de 25 jours de travail ;ou encore 5
000 € m’ont rapporté 300 € en un an et je veux savoir combien me
rapporterait dans le triple de temps une
somme de 30 000 € .
Dans tous les
cas le raisonnement est le même ; je cherche le résultat pour une unité , puis je le multiplie par le nombre d’unités .
Dans tous les
exemples précédents , les grandeurs sont dit
« directement proportionnelles » mais il y a des cas où la relation est inverse ;
ainsi : plus j’emploie d’ouvriers à
un travail , moins de temps il faudra
pour le finir . Plus un mur est haut , ou épais ,
moins de longueur on ne pourra en faire dans un temps déterminé ou avec une
quantité de matériaux donnée , on dit dans ce cas , que la règle de trois est inverse , car les
quantités sont inversement proportionnelles .
La règle de trois est simple
lorsque le problème se réduit à une seule relation ; et
elle est composée lorsque le problème comprend une série plus ou moins longue
de rapports .
Elle est
directe ou inverse selon que les
quantités sont directement ou inversement proportionnelles à la quantité
demandée.
La règle de
trois composée peut avoir à résoudre les
combinaisons les plus diverses de quantités directement et inversement proportionnelles
.
La Règle de Trois simple et
inverse :
Notion : la règle de trois simple
et inverse lorsque les quantités que l’on compare sont inversement
proportionnelles.
Ainsi je veux savoir combien je dois employer d’ouvrier pour faire un
travail en 7 jours au lieu de 9 ; quelle quantité de phosphate je dois employer par hectare de terrain si , avec
une quantité déterminée de ce produit , je veux fertiliser 8 hectares au lieu de 5 ; combien d’heures je dois
travailler par jour pour finir un travail en 6 jours au lieu de le faire en
8 ? Plus les enfants auxquels je distribue une boîte de bonbons sont nombreux , moindre sera le nombre des bonbons reçus par
chacun, etc.
Problème
type :
Si 30 ouvriers mettent 56 jours pour faire un ouvrage
, quel temps mettront 14 ouvriers pour faire le même ouvrage ?
|
grandeur |
Nombres
d’ouvriers |
Nombre
de jours |
|
1re
valeur |
30 ouv. |
56 j |
|
2e
valeur |
14 ouv. |
X j |
Méthode de réduction à l’unité
30 ouvriers mettent …………………………..56 j
1 ouvrier mettra 30 fois
plus de jours ou 56 j
30 ( = 1 680 j )
14 ouvriers mettront 14 fois moins de jours qu’un seul soit :
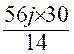= 120 jours
Autre solution : Le temps demandé
s’obtiendra en divisant le nombre de journées à fournir par le nombre des
ouvriers du 2e groupe .
1° le
nombre de journées à fournir égale :
56 j 30
2° le
nombre des ouvriers du 2e groupe égale 14
Les 14
ouvriers mettront donc 
= 120 jours pour faire
l’ouvrage .
TRAVAUX AUTO FORMATIFS.
Compléter la phrase suivante : la règle de
trois simple et inverse lorsque les …………………………………… ?.
1°) Un
robinet qui donne 10 litres par minute
met 18 heures pour remplir un bassin . Quel temps
mettrait-il pour le remplir si son débit était de 6 litres ? de 9 litres ? de 2 litres ;de
12 litres ?
2°) 10 ouvriers pourraient faire un ouvrage en 60 jours
, quel temps pour faire le même
ouvrage , 5 ouvriers ? 13 ouvriers ? 18 ouvriers ?
Problèmes :
a)
Combien faut-il d’ouvriers pour faire en 8 jours un
ouvrage que 24 ouvrier ont fait en 9 jours ?
b)
On a employé 34 kg de laine pour faire 25 m de
tissu qui a 60 cm de largeur. Si l’on avait tissé avec cette même quantité de
laine un tissus de 0,75 m de largeur , quelle longueur
d’étoffe aurait – on obtenue ?
c)
Avec 45 kg de fil de fer on fait un treillage de 36
m de long sur 1,20 m de large . Quelle aurait été la
longueur du treillage si la largeur n’eût été que 0,90 m ?
Compléter la phrase suivante : la
règle de trois simple et inverse lorsque
les quantités que l’on compare sont inversement proportionnelles.