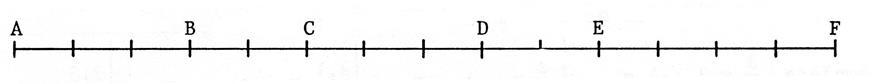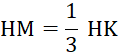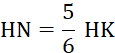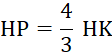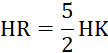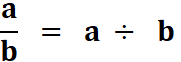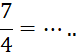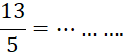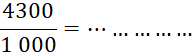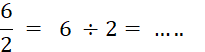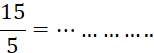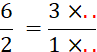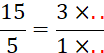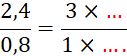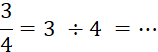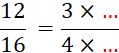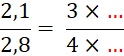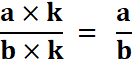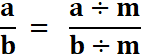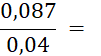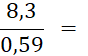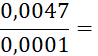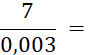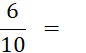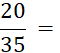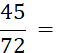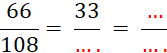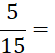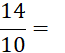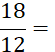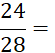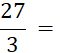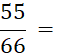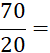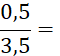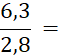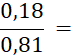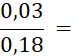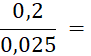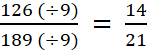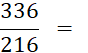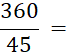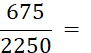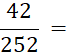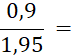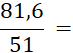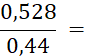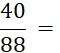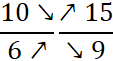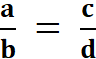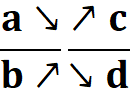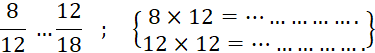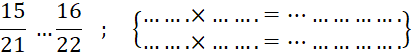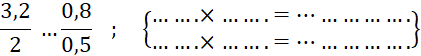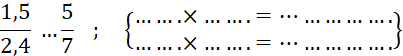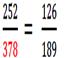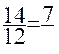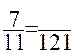Vers classe de 5^ème .

ACCES au CORRIGE.

I ) Pré requis:

Division : (notion)	.
Fraction : progression vue en primaire.	.
Information sur La fraction en arithmétique.	.
Fraction : unité	.
Pré requis : sur la fraction (pour niveau +++).	.
Lecture : la fraction ( nomenclature)	.

II ) ENVIRONNEMENT du dossier :

Index : warmaths

Objectif précédent : 1°) les nombres.

Objectif suivant : 1°) les 4 opérations Ensuite :les Opérations avec deux fractions. 3°) Valeur numérique d’une expression littérale 4°) Voir cours de niveau 5

1°)Tableau : 2°)Liste des cours 3°) les opérations sur les fractions . 4°) calcul numérique : la fraction.

III ) LECON

ECRITURE FRACTIONNAIRE d’UN NOMBRE

Chapitres :		Travaux spécifiques : niv VI et V
Fiche 1 : Travaux pré requis.
Fiche 2 : Ecritures fractionnaires d’un nombre.
Fiche 3 : Simplification d’une écriture fractionnaire.	Info + sur la simplification d’une fraction+
Fiche 4 : Exercices type de simplification d’écritures fractionnaires.
Fiche 5 : Propriétés des écritures fractionnaires d’un nombre
Fiche 6 : Inverse d’un nombre en écriture fractionnaire .
Fiche 7 : Pourcentage.
Fiche 8 : Organisation et gestion de données.
Revoir : cours niveau 5
Fraction	INFO 1 plus ! ! ! ! !	Dossier 138 - 139
Fraction décimale ; écriture décimale d’une fraction décimale et non décimale.	INFO 2 plus ! ! ! ! !	Dossier 150 et Dossier 151
Fractions égales ( équivalentes)	INFO 3 plus ! ! ! ! !	Dossier 160 et dossier 162 - 163
Multiplication d’une fraction par un nombre	INFO 4 plus ! ! ! ! !	Dossier 158 et Dossier 159
Calcul de durée ( système sexagésimal)	INFO 5 plus ! ! ! ! !	Dossier 173

IV) INFORMATIONS «  formation leçon » :

		Travaux auto -formatifs		INTERDISCIPLINARITE : voir cas par cas ! !
Test	COURS	Contrôle	Evaluation : Travaux complémentaires : Série 1 ; Série 2 ;Série 3	Sciences : - Les durées (n°1). - Calcul de temps ; de vitesse , de distance parcourue. - la vitesse uniforme.	CORRIGE :
			Travaux niveau VI et V sur les fractions Dos 138 - 139		Cours « élève »

Consigne : TRAVAILLEZ FICHE PAR FICHE .

COURS.
Fiche 1 : Travaux pré requis.
Vocabulaire : «  fraction » et « écriture fractionnaire » sont des « écritures fractionnaires ». Le mot « fraction » est réservé aux « écritures fractionnaires » dont les deux termes sont des nombres entiers . Exemples :
Activité 1 :
Complétez :
( 1 unité = 1 graduation)
Activité 2
· Placez les points « M » , « N » , « P » , « R » , tels que :
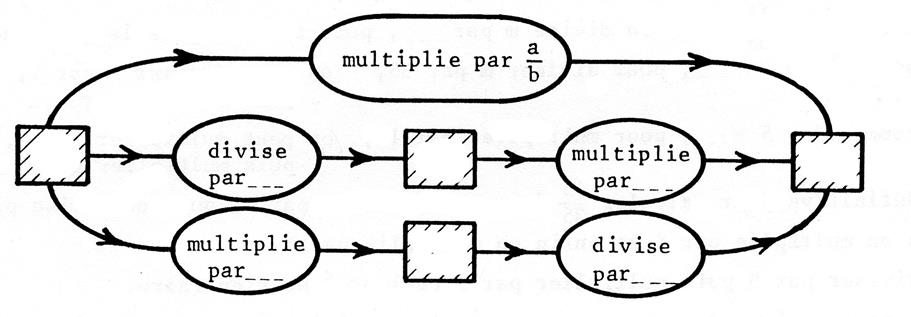
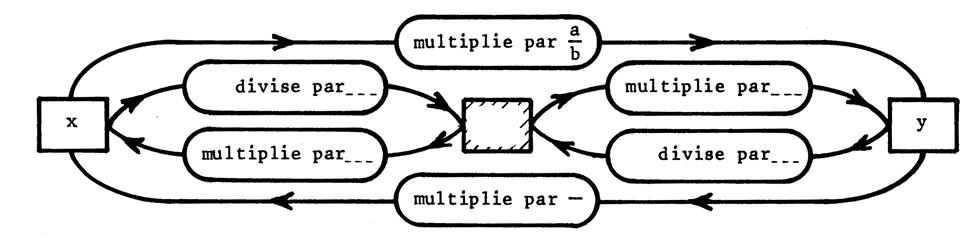
Complétez le schéma illustrant la multiplication par une fraction :
Activité 3 :	SOS : Multiplication d’une fraction par un nombre .
Calculez : les de 12	C'est-à-dire effectuez le produit : . soit ( 12 .. ) .. ; ou ; ( … …. ) 4 = ….. ………
Les
Les
Les
« a » et « b » étant des nombres entiers ou décimaux quelconques , « b  »
Activité 4 :
Ecrivez sous forme de nombre à virgule ( dit aussi : nombre décimal) . Exemple :
Remarque : pour multiplier par un nombre «  » , on peut multiplier ce nombre par le résultat de «  » Exemple : «   »  : devient :

Fiche 2 : Ecritures fractionnaires d’un nombre.
Complétez :
Vous pouvez écrire : sont des écritures fractionnaires d e l’entier naturel « 3 »
Vous constatez que :
Trouvez d’autres écritures fractionnaires de « 3 » : …………………………
· Complétez :
Vous pouvez écrire : ….
Vous pouvez alors écrire alors : ; ; sont des écritures fractionnaires du décimal « 0,75 »
Vous constatez que :;
Trouvez d’autres écritures fractionnaires de « 0,75 » : ……………………………………………………………..
· Considérons la fraction  ; Vous remarquez que « m » étant un nombre ( ou une grandeur) quelconque. Pour calculer «  «    on divise « m » par « … » , puis on multiplie le résultat par « ….. ». Remarques : Puisque «  » pour diviser « m » par « 35 » , on peut diviser « m » par « 7 » puis diviser par … .. Et comme «  15 = 5 ……… » , pour multiplier par « 15 » , on peut multiplier par « 5 » puis multiplier par « …... » En définitif (au regard de ce que l’on vient d’écrire) : Pour calculer les «  » de « m » , on divise « m » par « 7 » , puis on divise par « 5 » puis on multiplie par « 5 » et enfin on multiplie par « 3 ». Or « diviser par 5 » puis « multiplier par 5 »  revient à ne rien faire. Donc tout revient à diviser « m » par « ……… » puis multiplier le résultat par « ……. » . C'est-à-dire multiplier par la fraction « » Puisque « calculer les «  » de « m » revient à calculer les «  de m »  ; c’est que «  » et « »  représentent le même nombre.. · On peut écrire «  =  »
et comme		On a alors :
· Ce que l’on vient de faire avec le nombre « 5 » et «   »  , on peut le faire avec n’importe quel nombre « k » non nul et n’importe quelle écriture fractionnaire : ( b
Activité :
· On passe de «  à  » en multipliant les deux termes par .. …. · On passe de «  à  »  en divisant les deux termes de la fraction «  » par « ……… »….on alors que l’on simplifie par « 5 ». On écrira : qu’en généralisant :
				Avec «  »
A retenir : A partir d’une écriture fractionnaire d’un nombre, on obtient une autre écriture fractionnaire de ce nombre en multipliant ou divisant le numérateur et le dénominateur par un même nombre non nul.

Fiche 3 : Simplification d’une écriture fractionnaire.

Dire qu’une écriture fractionnaire est « plus simple » qu’une autre , c’est dire que son dénominateur et son dénominateur s’écrivent avec moins de chiffres ou sans virgule ou sont des entiers plus petits.

Exemple : Ci-contre on vous donne des écritures fractionnaires d’un même nombre.  ;  ;  ; Quelle est la plus simple ? ….…….

· Quand le dénominateur et le numérateur d’une écriture fractionnaire d’un nombre sont des décimaux , cette écriture fractionnaire peut être remplacée par une fraction. Il suffit de multiplier le dénominateur et le numérateur par « 10 » ; « 100 » ; « 1 000 » ; etc…… Faites-le dans les cas suivants :

· Simplification d’une fraction .

Sos : simplifier une fraction.

Pour simplifier une fraction, on divise (si cela est possible) le numérateur et le dénominateur par un entier non nul …

Exemple :

Considérons la fraction : , divisons chacun de ses termes par « 7 ».(sos  : table des « 7 » ) Divisons  : «  28 7 = 4 » ; «  21 7 = 3 » Appliquons : ; on peut donc écrire que En vous aidant de l’exemple ci-dessus : Simplifiez les fractions suivantes.

· Pour savoir si le dénominateur et le numérateur sont divisibles par un même nombre entier , vous pouvez utiliser les critères ( dit aussi : caractères ) de divisibilité.

· Caractères ( critères) de divisibilité.

Sos cours supplémentaires sur les…

Rappels : ( vu en classe de 6^ème) ; complétez le tableau ci-dessous.

Divisibilité par :

Condition nécessaire et suffisante.

« 10 ; 100 ; 1000 ;……. »

L’entier se termine par « …… » ; « ……. » ; « ……. » ; ….etc.

« 2 »

L’entier se termine par « …. » ; «….. » ; « …. » ; « …. » ; ou « …. » , il est dit « …… »

« 5 »

L’entier se termine par « …..» ou « ….. » ..

« 3 »

La « somme des chiffres » de l’entier est divisible par « ….. »

« 9 »

La « somme des chiffres » de l’entier est divisible par « …… »

· Fraction irréductible.

Sos cours : fraction irréductible..

Il se peut qu’une fraction ne soit pas (ou plus) simplifiable. Cela se produit quand le numérateur et le dénominateur n’ont pas de diviseur commun autre que le nombre « 1 ». On dit alors que la fraction est dite « irréductible ».

Exemples :

Il est possible de prouver ( et vous l’admettrez) que :

· Parmi les fractions représentant le même nombre non nul , il existe toujours une fraction irréductible et une seule.

Activité n° … :

Donnez la fraction irréductible des nombres suivants :

Avec des fractions.

Avec des écritures fractionnaires.

Remarque : « simplifier une écriture fractionnaire d’un nombre » sera très souvent synonyme (au collège) de « chercher la fraction irréductible représentant ce nombre ».

Fiche 4 : Exercices type de simplification d’écritures fractionnaires.
Exemple 1 : On vous propose de vous montrer comment simplifier la fraction
Procédure : Voici comment faire . - On remarque que « 504 » et « 756 » se termine par un multiple de « 2 » , ils sont « pairs ». Ils sont donc divisibles par « 2 » on a alors : - On remarque que « 252 » et « 378 » sont encore divisible par  « 2 » ; donc - Peut-on encore simplifier par « 2 » ? ……… - Nous allons regarder si les deux nombres « 126 » et « 189 » sont divisibles par « 3 ». Calculons la somme des chiffres de « 126 » = «  1 + 2 + 6 = 9 » ( « 9 » est divisible par « 3 » donc « 126 » est divisible par « 3 » ) ; Calculons la somme des chiffres de « 189 » = «  1 + 8 + 9 = 18 » ( « 18 » est divisible par « 3 » donc « 189 » est divisible par « 3 » ) ; - « 126 » et « 189 » sont divisibles par « 3 » , on peut donc simplifier la fraction par « 3 » : ; on remarque que les termes sont encore multiple de « 3 » ;en conclusion ; on pouvez simplifier la fraction par « 9 » : Peut-on encore simplifier par « 9 » ou par « 3 » ? …… …… ; Peut-on simplifier par « 5 » ? ……. …… - « 14 » et « 21 » ont encore un diviseur commun ( différent de « 1 ») qui est « 7 » … ; donc - Pratiquement on écrira : - Réponse :
Activité : simplifier, de même (c'est-à-dire jusqu’à les rendre irréductibles ) , les fractions suivantes :
Remarque : Dans le cas de  ; on commence par simplifier par «  100 » . On a alors   =
Dans le cas d’écritures fractionnaires ( au moins un terme contient un nombre à virgule) , on commence par se ramener à une fraction.
Exemple : soit à simplifier l’écriture : , on écrit alors : =
Activités : simplifier, de même (c'est-à-dire jusqu’à les rendre irréductibles ) , les écritures fractionnaires suivantes :
v Pour simplifier : on ne va pas effectuer les produits , mais au contraire. On va faire apparaitre des facteurs communs au numérateur et au dénominateur, pour ensuite supprimer les facteurs communs du numérateur et du numérateur. = on décompose : on supprime les facteurs communs :
Faites de même pour :
v Il est possible de prouver ( et vous l’admettrez …) que
Toutes les écritures fractionnaires d’un nombre s’obtiennent en multipliant numérateur et dénominateur de la fraction irréductible correspondante par un même nombre non nul.
Exemple : est irréductible . ; etc.
Activité : Trouvez toutes les fractions ayant un dénominateur inférieur à « 70 » et représentant le nombre dont une écriture est .
Activité : Trouvez la fraction ayant pour dénominateur « 15 » et représentant le nombre dont une écriture est :

Fiche 5 : Propriétés des écritures fractionnaires d’un nombre.
Dans la fiche « 2 » , vous avez vu comment on pouvait trouver d’autres écritures fractionnaires d’un nombre. Inversement, étant donné deux écritures fractionnaires, comment peut-on savoir si elles représentent le même nombre. ?
Simplifions : : = et , vous en déduisez que Calculez : ; ; vous constatez que :
On dit parfois que est l’égalité des « produits en croix »			Sos- produit en croix .
· Vérifiez que représentent le même nombre : …………. · Puis vérifiez en effectuant le produit en croix : 8 fois 21 = …. et 14 fois 12 = …..
Ce que vous venez de constater sur deux exemples , nous allons le prouver dans le cas général : on a : On peut écrire et comme alors Puisque représentent le même nombre et ont le même dénominateur , alors elles ont le même dénominateur donc : En définitive : s i alors
Inversement : Considérons deux écritures fractionnaires telles que Cherchons si . Puisque : alors et après simplification , En définitive , si : alors
ON résumera alors ces deux propriétés en un seul énoncé :
A retenir : « a », « b » , « c » , « d » sont des nombres et « b » et « d » sont des nombres non nuls ; Dire que : c’est dire que
On peut ainsi savoir si deux écritures fractionnaires représentent la même nombre. On vérifie l’égalité des « produits en croix »
Activité n° … :
Utilisez cette méthode dans les cas ci-dessous. Calculez les produits en croix , puis complétez en mettant le signe «   » ou «  »
Activité n° … :
Vérifiez que ; Avec les nombres « 12 », « 20 » , « 16 » ,  « 15 » , écrivez les « 4 » égalités différentes de la forme
Activité n°..
« x » et « y » sont des nombres tels que « 126 x = 108 y » Complétez : , donnez la forme simplifiée :
Activité n°..
Vous allez calculer le nombre « a » sachant que : Pour cela, écrivez l’égalité des produits en croix :
; vous en déduisez : , simplifiez , soit «  a = …. »

Fiche 6 : Inverse d’un nombre en écriture fractionnaire .					Sos : rappel sur l’opposé et l’inverse d’un nombre.
Exemple 1:
Complétez :
Exemple 2:
Complétez :
Réponses :
; l’inverse de est on peut ‘aussi’ dire que a pour inverse ;
Exemple 3:
Complétez par des fractions ( donnez l’écriture simplifiée ) :
Cas général : Considérons une écriture fractionnaire ( a 0 ; b 0 ) et désignons par « x » un nombre ( ou une grandeur ) quelconque. Le schéma ci-dessous montrez dans le cas général ce que vous avez constaté avec les 3 exemples précédents.
A retenir :
	« x » et « y » étant des nombres (ou des grandeurs) quelconques, et étant des écritures fractionnaires non nulles , dire que : «  y = x » c’est dire que «  x = y » , et sont dites inverses l’une de l’autre.
Activité n° … :
Quel est l’inverse ( Inv.) de :			Inv. =				Inv . =		Inv. =
Activité n° … :
L’inverse de est qui s’écrit plus simplement : « … »
Activité n° … :
Cherchons l’inverse de « 3 ». Vous savez que « 3 » peut s’écrit «  » Son inverse est donc : «   »
Activité n° … :
L’inverse de « 1,5 » est «  » , donnez –en une écriture fractionnaire simplifiée :
Activité n° … :
L’inverse de « 0,4 » est «  » , donnez-en une écriture décimale . soit :
Activité n° … :
L’inverse de « 0,001 » est , donnez –en une écriture entière :
Activité n° … :
Sachant que , calculez « E ».
E = = 105
Activité n° … :
On remplit les d’u réservoir avec 24 litres . Quelle est la capacité de ce réservoir ? Réponse : C = ; C = 56 litres
Activité n° … :
On partage une somme d’argent entre 2 personnes . La part de la première personne est les de la part de la deuxième. La première a reçu « 36 000 € » , quelle était la somme à partager ? ( conseil : Commencez par calculer la part de la deuxième personne)

Fiche 7 : Pourcentage.					Info : SOS cours sur les pourcentages
Rappel : vous avez vu dans la classe précédente que :
Calculer « 12 % » d’un nombre , c’est multiplier ce nombre par le fraction : ( remarque : cette fraction est la représentante du nombre décimale « 0,12 »)
Activité n° … :
Calculons les « 12% » de « 500 ». · =
Activité n° …
On sait que l’air contient ( en volume ) « 21% » d’oxygène. Combien y a-t-il d’oxygène dans une pièce dont le volume est de « 150 m^3 » ?
Activité n° …
Dans une classe de terminale, 80 % des élèves ont été reçus au baccalauréat. 1°) Il y avait « 35 » élèves dans cette classe. Combien d’élèves ( R ) ont été reçus ?
2°) Dans une autre classe, 75 % des élèves ont été reçus au baccalauréat. Il y a eu « 24 » reçus. Combien y avait-il d’élèves dans cette classe ? Appelons « E » le nombre d’élèves de la classe et « R » le nombre de reçus. On doit avoir «  R = E » . Vous en déduisez que « E = R » Nombre d’élèves de la casse :
3°) Dans une troisième classe , « 60 % » des élèves ont été reçus au baccalauréat. « 12 » élèves n’ont pas été reçus.. Combien y avait-il d’élèves dans cette classe ? S’il y a eu « 60 % » d’élèves reçus c’est qu’il y a eu «  100 % - 60 % = 40 % » d’élèves non reçus. Nombre d’élèves dans la classe :
Activité n° …
Au moment des soldes, un commerçant annonce un rabais de 30 % . Cela signifie qu’il fait une remise de du prix marqué. Si le prix est de « 100 € » , la remise est de « 30 € » . Le prix à payer est donc de …………….
1°) Le prix marqué est de 800 € . Calculez la remise et le prix à payer .
2°) Le prix marqué est de 170 € . Calculez la remise et le prix à payer .
3°) Le prix marqué est de 120 € . Calculez la remise et le prix à payer .
4°) Le prix marqué est de 255 € . Calculez la remise et le prix à payer .
5°) la remise est de 255 € . Calculez le prix marqué et le prix à payer .
6°) Le prix payé est de 350 € . Calculez le prix marqué et la remise . Si la remise est de 30 % du prix marqué , le prix payé est les « …… » du prix marqué.
7°) Le prix payé est de « 546 € ». Calculez le prix marqué et la remise. « 546 » représente les 70 % du prix à payer. Soit :
8°) Complétez le tableau suivant.
Prix marqué	100	1	50	72
Remise	30				3	18	82,5
Prix payé	70							14	560	88,2

Fiche 8 : Organisation et gestion de données.
L’Assemblée Nationale de la république Warmathsy comportent 450 députés répartis en 5 partis politiques dont le nom est une couleur. Le pourcentage de députés de chaque parti est donné par le tableau ci-dessous.
Députés	Assemblée	Parti rouge	Parti jaune	Parti vert	Pari bleu	Parti noir
Pourcentage		12 %	20 %	36 %	18 %	14 %
Nombre	450
Angle.	180°
1°) Calculez le nombre de députés de chaque parti , et complétez la ligne correspondante du tableau.
2°) Faites un histogramme représentant le nombre de députés de chaque parti. On a déjà tracé les axes de coordonnées , ci-contre .. Vous pouvez colorier les rectangles…………….
3°) Autre représentation :
Faites un diagramme « semi-circulaire » . Pour cela, utilisez le demi-disque ci-contre . Vous partagez ce demi-disque en 5 secteurs. Les angles de ces secteurs sont proportionnels aux nombres de députés . ( ou aux pourcentages). Le demi-disque représente les « 450 » députés , il correspond à « 180° ». Commencez par calculer l’angle de chacun des secteurs ( Complétez le tableau).
Exemple : le parti rouge représente les 12% de l’assemblée nationale. L’angle du secteur le représentant est donc
Après avoir dessiné les secteurs , vous pouvez les colorier………………………

ETUDE N°2

Demander les TRAVAUX d ’ AUTO - FORMATION sur : FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.

Leçon	Titre
N°2	TRAVAUX d ’ AUTO - FORMATION sur FRACTIONS – ECRITURE FRACTIONNAIRE - DUREE.

Consigne : compléter les phrases , les réponses sont dans le cours.

TRAVAUX N°2 d ’ AUTO - FORMATION : CONTROLE

Compléter les phrases suivantes :

1°) Fraction :

Il y a « fraction » ; si les …………………. nombres séparés par une ………………….. sont des …………………………...

Le nombre en dessous du trait de fraction appelé :…………………… il indique en combien de parties égales on divise une …………………..( appelé : …………………………..)

Le nombre au dessus du trait de fraction appelé ……………………..il indique combien on prend de ces parties .

2°) Ecriture décimale ou non décimale d’une fraction :

a) Ecriture décimale d’ une fraction décimale : Lorsque le dénominateur d’une fraction est 10 ; 100 ; 1000 ; …., nous avons ce que l’on appelle ……………………………… ; elles peuvent s’écrire sous forme d’une écriture ………………………. .

Une fraction est décimale si dans la division le quotient est ………………………..

b) Ecriture décimale d’une fraction non – décimale :

Une fraction est dite « non – décimale » si la division ne tombe pas juste .( le quotient ……………………….. )

La valeur décimale représentant la fraction non décimale est …………………………….. . On séparera la fraction et la valeur décimale arrondie par le signe « ……………. » qui se lit «  ……………….…. »

3°) fractions égales :

Des fractions sont égales si elles ont la même ……………………………….. ; .

Si on multiplie ……………………………………………..d’une fraction par un …………………………………….., on obtient une fraction égale .

Si on divise ………………………………………………….d’une fraction par un ……………………, on obtient une fraction égale .Dans ce cas ,on dit que l’on ……………………………….la fraction .

Un fraction est ……………………………. si elle ne peut plus être simplifiée.

4°) Multiplication d’une fraction par un nombre :

Citer les deux procédures que l’on peut utiliser pour multiplier une fraction et un nombre .

5° ) Calcul de durée ( système sexagésimal)

a) Comment procède - -t – on pour passer une durée exprimée en valeur sexagésimale en durée exprimée en valeur décimale ?

b) Comment procède - -t – on pour passer une durée exprimée en valeur décimale en durée exprimée en valeur sexagésimale ?

TRAVAUX N°2 AUTO - FORMATION : EVALUATION

Ecrire sur le doc.

1°) Exprimer par une fraction

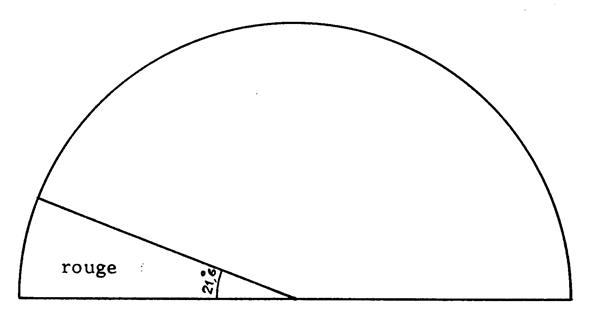
Quelle fraction d’aire représente la partie hachurée  ( unité 1 ) ?

0,5 =	0,5 =

0,5 =	0,5 =

0,5 =	0,5 =

2°) Ecriture décimale d’une fraction 

Donner la valeur décimale des fractions suivantes ( arrondir les valeurs à 0,001 prés si nécessaire)

	Résultat		Résultat

3°)Fractions égales :

série 1 : Trouver des fractions égales ; dont le dénominateur est 100.

	Résultat		Résultat

Série 2 :

Simplifier les fractions suivantes :

	Résultat		Résultat

Série 4 : compléter les fractions suivantes :

	Fraction :		Fraction :

4°) Multiplication d’une fraction par un nombre :

série 1 : effectuer les opérations suivantes puis simplifier le résultat :

=

=

=

Série 2 : Compléter le tableau : multiplier la fraction par le nombre , donner le résultat sous forme de fraction , ensuite sous forme décimale ( à 0,01 prés)

	2630	1240	1374	473
		3 fois 1240 = 3720 et 3720 / 5 = 7 44

5° La durée 

Convertir les durées suivantes ( arrondir à la minute près ; ou au 0,01 )

Dans le système décimal .	Convertir en ! ! !	Dans le système sexagésimal .
Heures , centièmes	Minutes	Heures , minutes
	135
12,66
		4 h 25 min
	2350
0,86
		1h 55 min

CD ³ Cliquer ici :PROBLEMES  Interdisciplinaires

MOTS à intégrer dans le contrôle :

1°)deux ; barre ; nombres entiers . : dénominateur ; quantité ; Unité ;numérateur

2°) Ecriture décimale d’une fraction :une fraction décimale   décimale .; exact.

3° Ecriture décimale d’une fraction non – décimale :

n’est pas exact ;le quotient arrondi . « » » ; «  peu différent de …. »

4°) fractions égales : écriture décimale .;le numérateur et le dénominateur ; même nombre , ; le numérateur et le dénominateur ; même nombre , ; simplifie ; irréductible .

Lorsque vous avez terminé ce travail ; passez à la correction (voir les documents papiers ou allez sur le site )