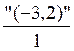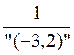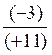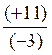Pré requis:

Nomenclature
Le nombre relatif

 

Index :   warmaths	opposé : Objectif précédent	opposé : Objectif suivant	INFO :   les nombres arithmétiques.   Liste des cours de calcul numérique
@  « inverse » en primaire.	Inverse : Objectif précédent	Inverse : Objectif suivant	Tableau         85
		1.     A consulter : Cours de collège en 5ème.
	2.         Cette leçon est très importante pour savoir comment on « neutralise un  terme » ou « un facteur »  , dans le cas des transformation d’égalité…

 

DOSSIER : OPPOSE et INVERSE d ' un nombre (cours) et  inverse d’une fraction.

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

 

 

Définition de l’objectif  : savoir écrire l’opposé et l’inverse d’un  nombre ou d’un terme, (  Ce  @ Cours   est  important pour  transformer une égalité ou résoudre une équation)

 

I )  Opposé d’un nombre (relatif):

           

         commentaire: on utilisera  l’opposé du nombre (ou d’un terme)  pour neutraliser un terme dans un membre d’une  égalité

 

         Notation: la notation mathématique de  « opposé  » d’un nombre  « a   »  est :  opp. a

 

         Procédure:         Pour obtenir l’ opposé  d’un nombre  (ou terme) il suffit de changer le signe  qui précède le nombre ou le terme.

 

         Résultats:      

                L’opposé de   +3    se notera   « opp. +3   »,on dira que l’opposé de +3 est  -3,ce qui se traduira en écriture mathématique:

     opp. (+ 3)  =  ( - 3)

 

                           

 

 

 

    L’opposé de  - 3  se notera  « opp. -3   » ,on dira que  l’opposé de  - 3 est +3,ce qui se traduira en langage mathématique:

 

opp. - 3 =  + 3

 

     L’opposé du terme 3x se notera  « opp. +3x   » ,on dira que l’opposé de  3x est  -3x ,ce qui se traduira par:

opp. 3x  = -3x

 

 

   Exemples:         opp. +3/5  =   - 3/5

                                  opp. -7    est  égal  à   +7

 

généralisation   :               opp.  a     =    - a

 

 

  Représentation graphique d’un nombre et de son opposé:

 

                   Pour donner la représentation graphique de l’opposé d’un nombre est un point .Il faut tracer une droite graduée (celle représentant les nombres relatifs ) dont le centre aura pour valeur  « 0 »

 

            pt. A’                                                  pt.A      

 

 

                                        (-x)                                                        (x )  

                 (- 3)                         0                          (+ 3)

 

    *On peut dire qu’un nombre et son opposé sont symétriques  par rapport  au  point  « 0 »,on dit aussi « symétrie centrale  »,(par rapport au centre « 0 » ).

 

 

   I I )     Inverse d’un nombre                                ( voir : la fraction archimédienne)

 

           commentaire  :  on a besoin de l’inverse d’un nombre  (facteur )pour pouvoir neutraliser un facteur  se trouvant dans un terme.

 

            Notation:

 

    La notation mathématique  de « l’inverse » d’un « facteur   a » ,ou d’un  nombre  est  «  inv. a  ».

 

      Par convention  :

 

       Pour obtenir l’inverse d’un  nombre il  faut construire une fraction de numérateur égal à 1 et de dénominateur égal à ce nombre ;

     

Procédure permettant  d’obtenir l’inverse d’un nombre:

 

 

Procédure :	Exemples numériques
1) mettre le nombre sous forme de fraction de dénominateur égal à  1 :   "a" =	"3" =    ; "3,2" =  ;  "(-3,2)" =
2)Inverser les "termes" de la "fraction": mettre le numérateur en dénominateur ; et mettre le dénominateur au numérateur	3" =    à pour inverse : "3,2" =  ; à pour inverse : "(-3,2)" = ; à pour inverse :
3) Rendre compte	Inv. 3" = Inv. "3,2" =  Inv. "(-3,2)" =

 

 

 

Traduction mathématique:

 

         de «  L’inverse de 3  est égale à la fraction    » est   « inv.3 = 1/3   »

 

  Généralisation:                    inv. a  =             (on peut écrire aussi :   1 / a )

 

 

 

     Autres exemples:

 

                 inv   (-3 ) =   1/ (-3)

                 inv    2x  =  1 / 2x

                         

 Représentation graphique de l’inverse d’un nombre:

 

La représentation graphique d l’inverse d’un nombre est un point situé sur une droite.

Soit l’inverse de « a »  =     1 / a       (que  « a » soit positif ou négatif ) le résultat est toujours inférieur à  1.

 

Remarque            :      inv. a / b    =    b / a              ou        inv.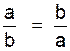

 

ce qui donne comme représentation graphique:

 

 

                                              0                      1               2                3     

 

 

 

                                                      inv. a = 1/3                      si         a = 3/1

 

                                                  pt  A’                                       Pt   A                 

 

 

Niveau plus :

 

 

L'inverse d'une fraction ou écriture fractionnaire:

 

 

L ' inverse de la fraction       (a / b )  est égal à la fraction    (b / a)

 

Ce qui se note :   inv   = 

 

commentaire  : on a besoin de l’inverse d’une fraction dans le cas de la division d'un fraction par une autre fraction .

 

Voir division de deux fractions

 

Nota: la fraction  est égale  à la multiplication du nombre "a" par l'inverse du nombre "b"  : on peut  écrire que   = a inv."b"

 

 

Procédure permettant de donner l'inverse d'une fraction: pour donner l'inverse d' une fraction  il suffit d'inverser le numérateur avec le dénominateur  , de la fraction.

 

Exercices exemples: 

 

 

Donner l 'inv.de ………	résultat
Inv.=
Inv.=
Inv.=
Inv.=
Inv.-=	-

 

 

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE  :

 

 

 

I )   OPPOSE:    (d’un nombre)

 

1)Donner un modèle d’écriture mathématique  de « opposé d’un nombre »

 

2)A quoi va servir l’opposé d’un nombre?

 

3)Traduire en langage mathématique:   opposé d’un nombre  « a » .

 

4)Donner la procédure permettant d’obtenir l’opposé d’un nombre.

 

5)Traduire en langage littéral:

                 5 _{1  )}             opp. a            :...........................................

                 5 ₂  )            opp  -a            :...........................................

 

 

 

 

 

II )  INVERSE:  (d’un nombre)

 

 

 

1)   A quoi va servir l’inverse d’un nombre?

 

2)    Traduire en langage mathématique:    inverse d’un nombre  « a »

 

3 )    Donner la procédure permettant d’avoir l’inverse d’un nombre.

 

4)   Traduire en langage littéral:

 

 

                                inv. a      =   inv.  a / 1    =   1 / a

 

 

5 )  inv. a / b    =    b / a

 

 

            EVALUATION :

 

I) Faire les exercices suivants :

 

 

opp. -5  =...................

 

opp  4   =..................

 

opp.  3 / 4 = ................

 

inv. 4       =...............

 

inv. 5 / 3 =................

 

inv.  -  5 / 3  =.................

 

inv. - 9         =......................

 

 

II)   Nommer  par une lettre majuscule les nombres  du premier membre  (voir égalités  EG1 et EG2)  suivants  et par une lettre majuscule  « prime » les résultats :( a    A     on associe  « A ‘ » )

Placer ces points    sur une droite graduée.

 

III)  Faire les exercices suivants:

 

inv. x   =        

 

opp. x  =

 

inv. a / b =

 

inv. ab / c =

 

                              inv. - x /3  =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CORRIGE EVALUATION :

 

 

 

I)Faire les exercices suivants :

 

 

opp. -5  =.......+5............

 

opp  4   =...........- 4.......

 

opp.  3 / 4 = ..- 3 / 4..............

 

inv. 4       =.....1 / 4..........

 

inv. 5 / 3 =.......3 / 5 ........

 

inv.  -  5 / 3  =........- 3 / 5.........

 

inv. - 9         =..........-1 / 9............

 

 

II) Nommer  par une lettre majuscule les nombres  du premier membre  (voir égalités  EG1 et EG2)  suivants  et par une lettre majuscule  « prime » les résultats :( a    A     on associe  « A ‘ » )

Placer ces points    sur une droite graduée.

 

III)Faire les exercices suivants:

 

II)Faire les exercices suivants:

 

inv. x   =      1 / x  

 

opp. x  =   - x

 

inv. a / b =    b / a

 

inv. ab / c =   c / ab

 

inv. - x /3  =     -3 / x

CONTROLE:

 

 

INVERSE:  (d’un nombre)

 

 

 

1)   A quoi va servir l’inverse d’un nombre?

on a besoin de l’inverse d’un nombre  (lorsqu'il est facteur )pour pouvoir neutraliser un facteur  se trouvant dans un terme.

 

2)    Traduire en langage mathématique:    inverse d’un nombre  « a » :   inv.a

3 )    Donner la procédure permettant d’avoir l’inverse d’un nombre.

1) mettre le nombre sous forme de fraction de dénominateur égal à  1 :   "a" =

2)Inverser les "termes" de la "fraction": mettre le numérateur en dénominateur ; et mettre le dénominateur au numérateur

3)Rendre compte

 

4)   Traduire en langage littéral:

                                inv. a      =   inv.  a / 1    =   1 / a

l'inverse d'un nombre "a" est égal à l'inverse de la fraction  de numérateur égal à "a" et de dénominateur égal à un ;est égal à la fraction de numérateur égal à 1 et de dénominateur égal à "a".

5)   A quoi va servir l’inverse d’une fraction ?

on a besoin de l’inverse d’une fraction dans le cas de la division d'un fraction par une autre fraction .

6)  inv. a / b    =    b / a

7 )    Donner la procédure permettant d’obtenir  l’inverse d’une fraction

pour obtenir  l'inverse d'une fraction  il suffit d'inverser le numérateur avec le dénominateur  , de la fraction.

 

                   EVALUATION :

 

inv.(+ 4)       =.....1 / (+4)..........

 

inv. (5 / 3) =.......(3 / 5) ........

 

inv.  (-  5) /(+ 3)  =........(+ 3) / (-5) .........

 

inv. (- 9)         =..........1 / (+9)............

 

inv.(+5)/(-3)     = (-3) /(+5)

 

 

Niveau +