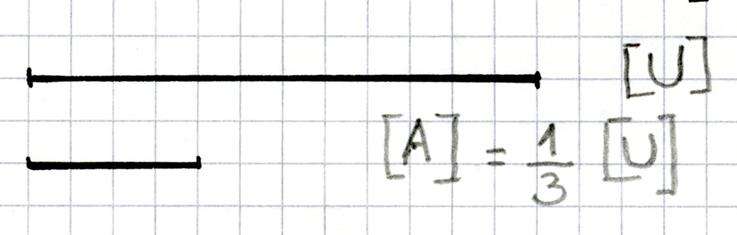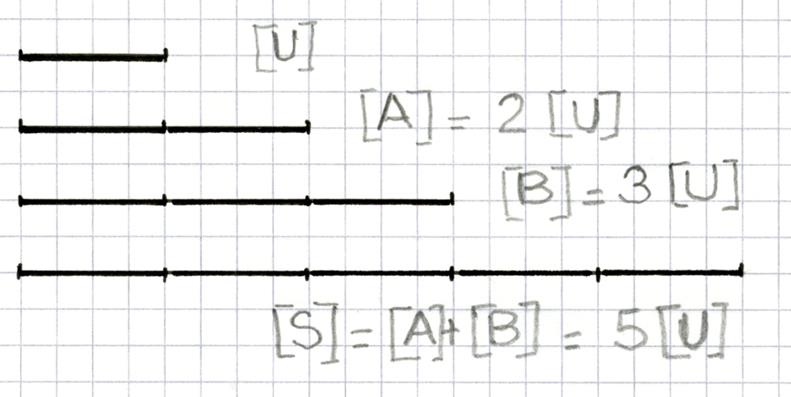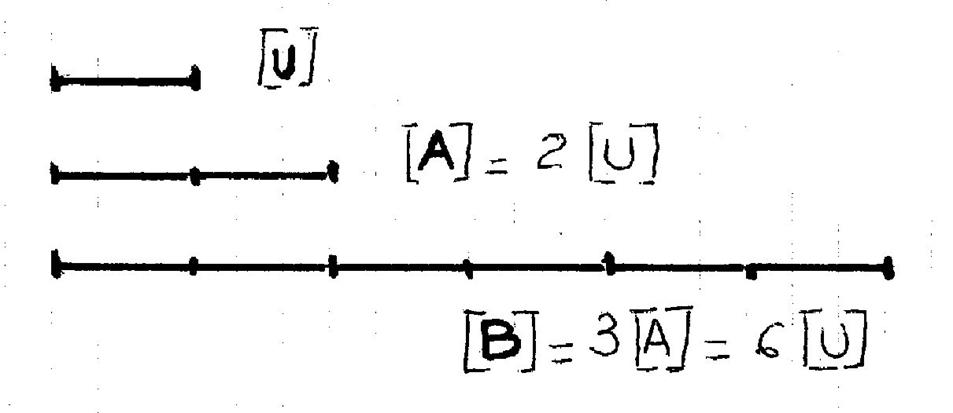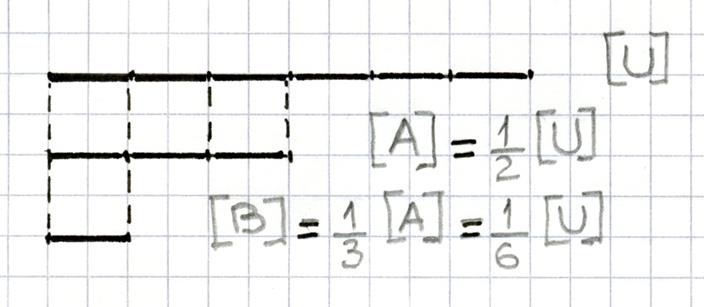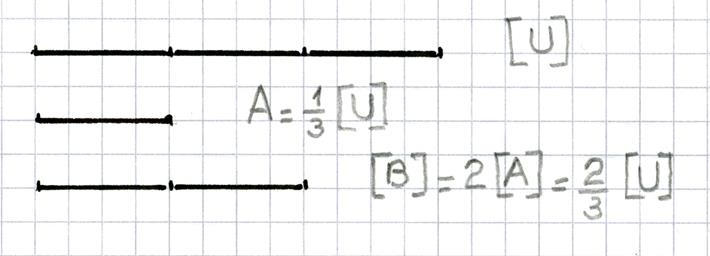COURS

I ) Définitions des nombres arithmétiques

a) multiplication d’un segment par un nombre entier.  ( info ++++) 

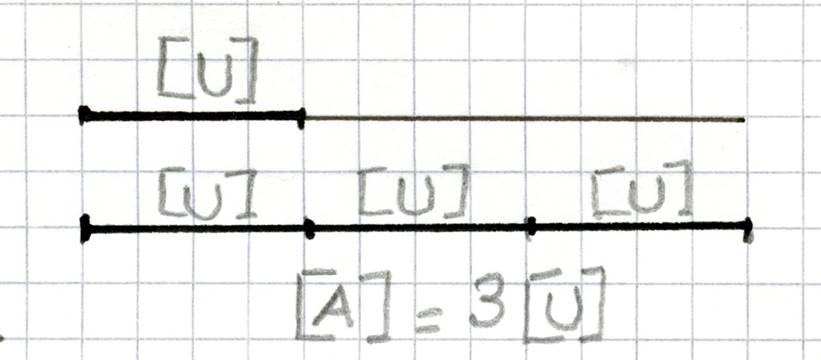
Soient  un segment «[ U ] » et le nombre « 3 ». ( voir ci -contre)

On peut construire le segment « [ A ] » en portant sur une droite trois segments consécutifs égaux à « [ U ]».  « [ A ]  »  est le produit du segment « U » par le nombre « 3 »

On peut écrire : «[ A ]  = 3 . [ U ] »

(lire  « A est égal à 3 fois U »)

b) Notion d’opérateur entier .

Le nombre « 3 par lequel on a multiplié le segment « [ U ] » pour obtenir le segment « A » est un opérateur entier.

Quel que soit le nombre entier « n » ce nombre entier peut être considéré comme un opérateur . ON écrit :  « A = n . [ U ] »

c) Opérateur archimédien.

1°)  Le nombre « 3 » est l’opérateur qui permet de passe du segment « [ U ]» au segment « A ».(voir figure ci-dessus) . L’opérateur permettant de passer du segment « [ A ]  » au segment «[ U ] » est l’opérateur inverse de « 3 ».

On désigne cet  opérateur  inverse de « 3 » par la notation : «  » 

( 1 )

[ A ]  = 3 . [ U ]

[ U ] =  [ A ] 

2°)  De façon générale :

Les opérateurs archimédiens sont les opérateurs inverses des nombres entiers.

Si « p » est un nombre entier, et si « A » et « B » désignent des segments , on a l’implication réciproque .

( 2 )

[ B ]  = p . [ A ] 

[ A ]  =  [ B ]

d) Fractions archimédiennes.

On convient de dire que l’opérateur  archimédien «  »    est un nombre bien qu’en fait il soit composé de deux nombres.

Les opérateurs archimédiens   sont donc des nombres.

Les nombres  de la forme  «  » sont appelés des fractions archimédiennes.           ( voir : info++)

e) l’ Axiome d’Archimède.

                                             Un segment « [ OA ] » et  un nombre entier « p » étant donnés, il existe sur le segment « [ OA ]» un point « B » et un seul tel que :   «  p . [ OB ]= [ OA ] » 

Cet énoncé constitue l’axiome d’ Archimède. 

f ) Multiplication d’un segment par une fraction archimédienne.

Nous avons vu ( @ 2 ci-dessus)) :    p . [ O B ] =  [ O A ]     [ OB ]  =  [ OA ]

Le segment [ O B ]  est le produit du segment  [ OA ]  par la fraction archimédienne «  »

Exemple :  ( voir ci contre)

Soit le segment [ U ]  et le nombre   le segment [ A ] , ou tout autre segment égal, est le produit de  [ U ]  par    .

f ) Nombres arithmétiques.

Le procédé utilisé pour inventer les fractions archimédiennes permet  de généraliser la  notion de nombre :

Tout opérateur qui permet de passer d’un segment [A] à un autre segment [B]  est un nombre arithmétique.

On invente de cette manière les nombres arithmétiques ; parmi ces nombres  arithmétiques figurent évidemment les nombres entiers et les fractions archimédiennes ; mais aussi les fractions ordinaires et les fractions décimales et d’autres nombres ( nombres irrationnels) .

B) Les opérations avec des nombres arithmétiques.

1°) Addition des nombres arithmétiques.

·      Soient un segment [ U ] et les deux nombres entier « 2 » et « 3 »  ( voir figure ci contre)

On construit les segments :  

[ A ]   =  2 . [ U ]    et      [ B ]  = 3 .  [ U ]

ainsi que leur somme :

On remarque que :        [ S ]   =  5 . [ U ]

Donc :  2 . [ U ]   +   3 . [ U ]  =  ( 2 + 3 ) . [ U ]

De façon plus générale si « a »  et « b » sont deux nombres entiers on a :

a . [ U ]   +   b . [ U ]  =  ( a + b ) . [ U ]

( 3)

·      Ceci amène à donner la définition suivante :

            Soit un segment  [ U ]  et deux nombres arithmétiques quelconques « a » et « b ». On construit les segments : [ A  ]  = a    [ U ]  et   [ B ] = b . [ U ]

Ainsi que leur somme :  [ S ]  =  [ A  ] +  [ B ]

L’opérateur « s » permettant de passer directement du segment   [ U ]  au   segment   [ S ] est la somme des nombres « a » et « b »

On pose :  s = a + b ;

On a donc , quels que soient les nombres arithmétiques é »a » et « b » :

a . [ U ]   +   b . [ U ]  =  ( a + b ) . [ U ]

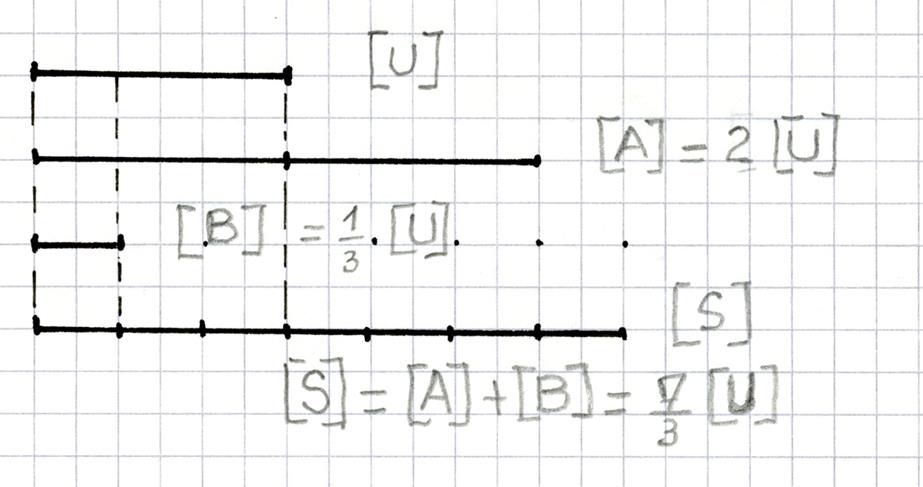
Exemple : Calculer la somme des nombres :  « a = 2 » et « b=  » 

On obtient  facilement la figure ci contre :

·      2 . [ U ]   +    . [ U ]  =  ( a + b ) . [ U ].

·      [ S ]  =  [ A  ] +  [ B ]

 avec   :   [ A  ]   = 2  [ U ] ;   [ B ]  =   [ U ]

On voit sur cette figure que « s =  »

On a donc :  2  +     = 

2°) Multiplication des nombres arithmétiques.

1°)  Soient un segment  [ U ] et les deux nombres entiers « 2 » et « 3 » On construit les segments :

[ A ]   =  2 . [ U ]  et     [ B ]  =  3 . [ A ]

On remarque  que :  [ B ]   =  6 . [ U ]

Donc : 3 .( 2 . [ U ] ) =  ( 3 . 2 )  . [ U ]

De façon générale, si « a » et « b » sont deux nombres entiers, on a :

«  b . ( a [ U ] )  =  ( b . a )  . [ U ]           ( 4 )

2°)  Ceci amène à donner la définition suivante :

Soient un segment  [ U ] et les deux nombres entiers « a » et « b » On construit les segments :

[ A ]   =  a . [ U ]  et     [ B ]  =  b.  [ A ] ;          Donc : b .( a . [ U ] )

L’opérateur « p » permettant de passer directement de  [ U ]  à     [ B ]  est le produit des nombres « a » et « b ».

On pose :                  «  p = b . a »

On a donc , quel que soient les nombres arithmétique  « a » et « b » :  «  b . ( a [ U ] )  =  ( b . a )  . [ U ]            ( 5 )

Exemple : Calculer le produit des nombres :  « a =  » et « b=  »

On construit d’abord : [ A ]   =   . [ U ]  et     [ B ]  =   . [ A ]

On obtient facilement la figure ci-contre.

On voit que sur cette figure que « p =  » . On a donc .

                      «   .   =    »

3 °) Opérateurs fractionnaires .

1°) Soient un segment [ U ]  et les nombres « a=  »  et « b = 2 » ( figure ci-contre)

On construit les segments : 

[ A ]   =   . [ U ]    et    [ B ]  =  2  . [ A ]   

[ B ] =  2 .  . [ U ]

On passe directement du segment  [ U ]    au segment    [ B ]  par un opérateur « p » produit des opérateurs : «  »  et  « 2 » 

«  p =  2   »          ; on pose       «  2   =    »   ; on dit que  «     »  est un opérateur fractionnaire.

2°) Ce-ci amène à donner la définition suivante :

Le produit d’un opérateur archimédien «  » et un opérateur entier « n » est un opérateur fractionnaire.

On note :

« n .  =  »

4 °) Fractions arithmétiques .         ( info : la fraction …)

L’opérateur  «     »  est un nombre arithmétique..

Les opérateurs fractionnaires « » sont appelés des « fractions arithmétiques »

Le nombre « n » est le numérateur et le nombre « p » est le dénominateur de la fraction.

Le numérateur et le dénominateur sont les termes de la fraction.

L’ensemble des nombres entiers et des fractions constitue l’ensemble des nombres arithmétiques rationnels.

5°) Multiplication d’un segment par une fraction.

Le segment  [ B ]  obtenu ( chapitre : opérateurs fractionnaires)  est le produit du segment  [ U ] par  «      ». On pose :  [ B ] =  [ U ]

De façon générale :

[ B ] = n .  ( [ U ])

[ B ] = ( n  x   )  [ U ]

[ B ] =   [ U ]

est le produit du segment   [ U ]  par la fraction

6°) Nombre égaux . Nombres inégaux.

·      Deux nombres arithmétiques sont égaux ( ou équivalents) si , considérés comme opérateurs agissant sur un  même segment [ U ] ils donnent des segments –produits égaux.

·      Si les segments- produits sont inégaux, les deux nombres sont inégaux. Le plus grand nombre est celui qui donne le plus grand segment.

CONTROLE:

Relire  et s’imprégner du cours

EVALUATION: