Pré requis:

l ' addition dans N

ENVIRONNEMENT du dossier :

Index warmaths	Objectif précédent 2°) la multiplication 3°) La table de Pythagore.	Objectif suivant : 1°) Les tables et l’écriture en algèbre .. 2°) La multiplication	Tableau 19 · Fiches d’arithmétiques à consulter · Liste des cours de calculs numériques
		3°) Puissance 1 (les carrés parfaits)

Par nécessité (pour pouvoir appréhender les mécanismes de penser en algèbre (dans la résolution d’une équation) et pour effectuer la division ) il faut connaître par cœur les tables de multiplication.

Une des méthodes est celle de « l’imprégnation cérébrale » , c'est-à-dire : la répétition ligne par ligne ( chaque ligne répétée au minimum 20 fois , sans réfléchir ) , réciter ensuite la table dans l’ordre croissant , par ordre décroissant , et en désordre .

Et ainsi de suite …….. » tout bêtement ».

Tous les élèves sont capables de retenir les tables , encore faut-il leur faire apprendre et les faire « se souvenir » ….en les appliquant , avec la nécessité de ne pas employer la calculatrice lorsque l’on doit faire apprendre des méthodes qui servent à « apprendre à compter » .

DOSSIER :

TABLES de MULTIPLICATION dans N (les entiers naturels) et la table de Pythagore

				Tout sur la multiplication : fiches d’activités.
Ici : TEST sur les opérations : les multiplications	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Fiches à consulter	Corrigé Contrôle	Corrigé évaluation
Impératif : toutes les personnes doivent être prévenues qu’elles sont obligées de passer le test sur les tables de multiplications. Aucune progression n’est autorisée si ce test n’est pas validé ( le nombre d’erreurs ne doit pas dépasser « 4 »)

TESTS OBLIGATOIRES :

Remarque : LES TABLES DE MULTIPLICATIONS de 1 à 10 sont à savoir "par cœur" ,il est inutile de continuer la progression tant que cet obstacle n'aura pas été franchi.

Consignes pour faire passer le TEST :

Faire tracer un tableau de 6 lignes et 10 colonnes ( = 60 cases)

Il est dicté par le formateur (ORAL) ; lire « ligne par ligne » , les résultats sont copiés dans l’ordre ( 10 réponses par ligne , laisser un espace , si on ne connaît pas le résultat demandé .

Soit 6 lignes de 10 réponses à comparer avec le corrigé.

seules des réponses sont copiées sur la feuille à rendre à corriger , ( voir le corrigé ci dessous  le tableau) :

Autre méthode :

Prendre une feuille blanche, mettre le nom prénom , Classe , date , tirer un trait horizontal . Ensuite , tirer 3 traits « verticaux » et écrire le résultat , l’un en dessous de l’autre . descendre ligne par ligne en suivant le trait . (le premier résultat en haut à droite), descendre en longeant le trait , revenir au deuxième trait et redescendre de nouveau , ainsi de suite, un résultat l’un en dessous de l’autre , passer une ligne si vous ignorez la réponse.

1010	66	58	86	35	73	64	85	79	33
52	63	72	77	88	45	67	22	25	96
74	48	56	26	82	34	75	83	29	59
84	68	54	23	39	95	47	65	46	92
78	97	37	6 ´ 0	53	87	76	55	43	36
4 4	82	89	93	99	27	62	710	98	69

Correction :

100	36	40	48	15	21	24	40	63	9
10	18	14	49	64	20	42	4	10	54
28	32	30	12	16	12	35	24	18	45
32	48	20	6	27	45	28	30	24	18
56	63	21	0	15	56	42	25	12	18
16	16	72	27	81	14	12	70	72	54

Si problème : remplir le tableau suivant :

A l’intersection d’une ligne et d’une colonne existe une case vide ,la remplir ,y indiquer la valeur du nombre qui est obtenue par la multiplication du nombre de la ligne avec la ligne de la colonne .(voir ci dessous pour les réponses )

1	2	3	4	5	6	7	8	9
2
3
4
5
6
7
8
9

COURS

Tables de multiplication 

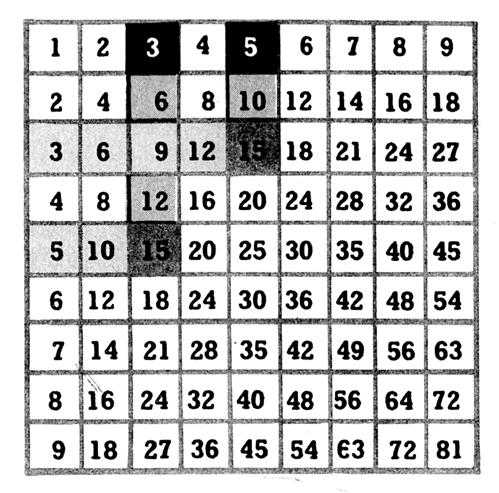
Ci contre : la table de « Pythagore » : Nous considérons le nombre en tête de ligne L (« 6 ») et la colonne « 8 » Dire combien de fois le produit choisi dans la ligne (« 6 ») renferme le nombre en tête de colonne , ( « 8 ») :nous trouvons : «  48 » Ainsi ; en « 48 » il y « 6 » fois le nombre « 8 » . Ou pour « 8 » fois « 6 » ; à l’intersection de la ligne et la colonne on trouve « 48 »

Savoir construire "La table de Pythagore".

Pour multiplier un nombre par un autre nombre, il faut savoir de mémoire la table de multiplication. Cette table , dite de « Pythagore » ,renferme les produits de deux quelconques des neufs premiers nombres . ( de 1  à 9 )

1	2	3	4	5	6	7	8	9
2	4	6	8	10	12	14	16	18
3	6	9	12	15	18	21	24	27
4	8	12	16	20	24	28	32	36
5	10	15	20	25	30	35	40	45
6	12	18	24	30	36	42	48	54
7	14	21	28	35	42	49	56	63
8	16	24	32	40	48	56	64	72
9	18	27	36	45	54	63	72	81

Construction de la table : Pour construire la table de Pythagore , on écrit sur une même ligne et de gauche à droite les neufs premiers nombres .

On obtient la 2^e ligne en ajoutant à eux – mêmes les nombres de la première . On obtient la 3^e en ajoutant les nombres de la 1^re à ceux de la 2^e . On obtient la 4^e en ajoutant les nombres de la 1^re à ceux de la 3^e , et ainsi de suite .

Manière de s’en servir : Soit à multiplier 5 par 8 . On suit la 5^e colonne verticale , jusqu’à la 8^e ligne horizontale .

Le nombre « 40 » ainsi trouvé est le produit cherché .

On serait arrivé au même résultat en suivant la 8^e colonne verticale jusqu’à la 5^e ligne horizontale .

CONSTRUCTION DES TABLES DE MULTIPLCATION:

Table des deux :

Opération: Lire: "2 fois.."	Egal	Correspond à l'addition
21	2	2 ou 1+1
22	4	2+2 ou 2+2
23	6	2+2+2 ou 3+3
24	8	2+2+2+2ou 4+4
25	10	2+2+2+2+2ou 5+5
26	12	2+2+2+2+2+2 ou 6+6
27	14	2+2+2+2+2+2+2 ou 7+7
28	16	2+2+2+2+2+2+2+2 ou 8+8
29	18	2+2+2+2+2+2+2+2+2 ou 9+9
210	20	2+2+2+2+2+2+2+2+2+2 ou 10+10

Table des trois

Opération	Egal	Correspond à l'addition
31	3	1+1+1 = 1fois3
32	6	2+2+2 =2 fois3
33	9	3+3+3
34	12	4+4+4
35	15	5+5+5
36	18	6+6+6
37	21	7+7+7
38	24	8+8+8
39	27	9+9+9
310	30	10+10+10

Table des quatre

Opération	Egal	Correspond à l'addition
41	4	1+1+1+1
42	8	2+2+2+2 =2fois 4
43	12	3+3+3+3 =3fois4
44	16	4+4+4+4
45	20	5+5+5+5
46	24	6+6+6+6
47	28	7+7+7+7
48	32	8+8+8+8
49	36	9+9+9+9
410	40	10+10+10+10

Table des cinq

Opération	Egal	Correspond à l'addition
51	5	1+1+1+1+1
52	10	2+2+2+2+2=2fois5
53	15	3+3+3+3+3=3fois5
54	20	4+4+4+4+4=4fois5
55	25	5+5+5+5+5
56	30	6+6+6+6+6
57	35	7+7+7+7+7
58	40	8+8+8+8+8
59	45	9+9+9+9+9
510	50	10+10+10+10+10

Table des six

Opération	Egal	Correspond à l'addition
61	6	1+1+1+1+1+1 =1fois6
62	12	2+2+2+2+2+2= 2fois6
63	18	3+3+3+3+3+3=3fois6
64	24	4+4+4+4+4+4=4fois6
65	30	5+5+5+5+5+5=5fois6
66	36	6+6+6+6+6+6
67	42	7+7+7+7+7+7
68	48	8+8+8+8+8+8
69	54	9+9+9+9+9+9
610	60	10+10+10+10+10+10

Table des sept

Opération	Egal	Correspond à l'addition = à déjà vu dans la table des:
71	7	1+1+1+1+1+1+1 =1fois7
72	14	2+2+2+2+2+2+2=2fois7
73	21	3+3+3+3+3+3+3=3fois7
74	28	4+4+4+4+4+4+4=4fois7
75	35	5+5+5+5+5+5+5=5fois7
76	42	6+6+6+6+6+6+6=6fois7
77	49	7+7+7+7+7+7+7
78	56	8+8+8+8+8+8+8
79	63	9+9+9+9+9+9+9
710	70	10+10+10+10+10+10+10

Table des huit

Opération	Egal	Correspond à l'addition
81	8	1+1+1+1+1+1+1+1=1fois8
82	16	2+2+2+2+2+2+2+2=2fois8
83	24	3+3+3+3+3+3+3+3=3fois8
84	32	4+4+4+4+4+4+4+4=4fois8
85	40	5+5+5+5+5+5+5+5=5fois8
86	48	6+6+6+6+6+6+6+6=6fois8
87	56	7+7+7+7+7+7+7+7=7fois8
88	64	8+8+8+8+8+8+8+8
89	72	9+9+9+9+9+9+9+9
810	80	10+10+10+10+10+10+10+10

Table des neufs

Opération	Egal	Correspond à l'addition
91	9	1+1+1+1+1+1+1+1=1fois9
92	18	2+2+2+2+2+2+2+2=2fois9
93	27	3+3+3+3+3+3+3+3=3fois9
94	36	4+4+4+4+4+4+4+4=4fois9
95	45	5+5+5+5+5+5+5+5=5fois9
96	54	6+6+6+6+6+6+6+6=6fois9
97	63	7+7+7+7+7+7+7+7=7fois9
98	72	8+8+8+8+8+8+8+8=8fois9
99	81	9+9+9+9+9+9+9+9
910	90	10+10+10+10+10+10+10+10

Table des dix:

Opération	Egal	Correspond à l'addition
101	10	1+1+1+1+1+1+1+1+1
102	20	2+2+2+2+2+2+2+2+2
103	30	3+3+3+3+3+3+3+3+3
104	40	4+4+4+4+4+4+4+4+4
105	50	5+5+5+5+5+5+5+5+5
106	60	6+6+6+6+6+6+6+6+6
107	70	7+7+7+7+7+7+7+7+7
108	80	8+8+8+8+8+8+8+8+8
109	90	9+9+9+9+9+9+9+9+9
1010	100	10+10+10+10+10+10+10+10+10

L'ensemble de ces tables est à savoir entiérement "par cœur"

Il est important de savoir "construire"une table de multiplication: de la forme :

"b" fois un nombre =

"b" est utilisé dans la division euclidienne

Table des "b"	Exemple: table des "31"
"b" fois 0 =	31 0 = 0
"b" fois 1 =	311 =31
"b" fois 2 =	312 = 62
"b" fois 3 =	313 =93
"b" fois 4 =	314 =124
"b" fois 5 =	315 =155
"b" fois 6 =	316 =186
"b" fois 7 =	317 =217
"b" fois 8 =	318 =248
"b" fois 9 =	319 =279
"b" fois 10 =	3110 = 310

PRESENTATION de l ‘ opération «  multiplication »:

Mots directement associés à la multiplication :

multiplicande ; multiplicateur ; produit ; facteur ;

L 'OPERATION :

La multiplication est une opération qui associe deux nombres ; en vue d ’ en obtenir un troisième. ( appelé : résultat ) .

MULTIPLICANDE ; MULTIPLICATEUR ; FACTEUR :

L ’ un des nombres s ‘appelle : « multiplicande »,l ‘autre nombre « multiplicateur » ; les deux nombres (situés à la droite et à la gauche du signe multiplier) s’appelle : « facteur »

Le premier nombre nommé est le nombre « multiplié » il s’appelle « multiplicande ».

Le deuxième nombre est celui qui multiplie le multiplicande ; il s ’ appelle le « multiplicateur ».

PRODUIT :

Le résultat de la multiplication s ’ appelle : « produit ».

En RESUME :

multiplicande multiplicateur = produit

multiplicande	« par » ou « fois »	multiplicateur	égal	produit
5		8	=	40
8		5	=	40

La multiplication se substitue à une suite additions d ’ un même nombre (multiplicande) dont la répétition est donné par la valeur du multiplicateur.

Exemple : j ’ achète 3 paquets de 4 plaques de chocolat de 100 grammes ; combien ai - je de plaques ?

solution 1 : par addition : j’ai 4 + 4 + 4 = 8 +4 = 12 plaques

solution 2 : par la multiplication : j ‘ai 3 4 = 12 ( d’après les tables)

Disposition pratique de la multiplication :

multiplicande

multiplicateur

« produit »

Se souvenir que  :

L ‘ élément neutre de la multiplication :

L ’ élément neutre de la multiplication est « 1 »

parce que « 1» fois « quelque chose » égal « quelque chose  » ; soit 1n =n

L ’ élément absorbant de la multiplication :

L ’ élément neutre de la multiplication est « 0 »

parce que « 0 » fois « quelque chose » égal « 0 » ; soit 0n = 0

Pratique de la multiplication :

A ) Le multiplicateur est à « un chiffre » :

I ) Première approche :

exemple : 476 5 =

Voir Objectif : Numération :

le 6 représente : 6 unités d'unités ; le 7 représente 7 dizaines d 'unités ; le 4 représente 4 centaines d ' unités

Donc le nombre 476 se décompose sous forme d ‘ additions : 400 + 70 + 6

donc Multiplier 476 par 5 : revient à faire les opérations suivantes :

On décompose 476 en additions 400 + 70 +6

On multiplie chaque terme (PAGE: 9
Un terme est un nombre situé à droite ou à gauche du signe "+" ) par « 5 » : (400 5) + ( 70 5) + (6 5) =

On effectue les Calculs :

400 5 = 2000

70 5 = 350

6 5 = 30

On additionne  2 000 + 350 + 30 pour obtenir = 2 380

Donc on peut écrire que 476 5 = 2 380

II ) Deuxième approche

Il  suffit de multiplier chaque chiffre du multiplicande par celui du multiplicateur en commençant par la droite et de « porter » la retenue à la colonne suivante.

1 7 2 8

4

= 6 9 1 2

Description du calcul :

On fait : 4 8 = 32 ; je pose 2 et je retiens « 3 »

je calcule 4 2= 8 (+3) = 11

je pose « 1 » et je retiens « 1 »

je calcule 4 7 = 28 (+1) = 29 je pose 9 et je retiens 2

je calcule 4 1 =4 ( +2) =6

TRAVAUX AUTO - FORMATIFS.

PREPARATION du CONTROLE

1°)Que signifie le symbole :

2°)Comment appelle - t on les nombres situés à droite et à gauche du signe

3°)Que pouvez vous dire sur ce qu ‘est un multiplicande et un multiplicateur ?

4°) Donner la disposition pratique de la multiplication .

5°)Quel est l ' élément neutre de la multiplication ?

6°)Quel est l élément absorbant de la multiplication ?

PREPARATION EVALUATION :

EXERCICES à faire sur feuille ; vérification ensuite à la calculatrice.

I ) Effectuer les additions suivantes :

a	16 8	c	756	d	45 7	e	830 9
f	256 27	g	485 58	h	849 95	i	358 24
j	1 694 58	k	3 27443	l	2 38039	m	8 76473
n	76 465932	p	46 178375	q	76 548654	r	56 381784

II ) Calculer:

a	425 4	b	237  5
c	807 46	d	198 27
e	9 087 97	f	2 783 64
g	54 639499	h	98 569 531

III ) Calculer:

a	8317	b	217 4
c	573 81	d	78297
e	6 781  21	f	147018
g	20 682 702	h	80 987 614

IV ) Calculer

a	630 3	b	427  6
c	632 19	d	942 72
e	4 29127	f	5 431 86
g	56 045 792	h	59 234 321

INTERDISCIPLINARITE:

ENCADREMENT d'un nombre "non divisible" dans la table des multiplications:

Exemple : Répondre à la question : Dans "13" il y a combien de fois "2" ?

Réponse : Il faut , avant de répondre (réponse : 2 fois 6 reste 1) ; se réciter la table des multiplication des "2" et reconnaître que 13 est compris entre "2 fois 6 et 3 fois 6 )

Nous avons effectuer un encadrement :

La réponse dépend de ce que l'on sait : que « 13 » est compris entre 2 fois 6 et 2 fois 7 , dans la table des « 2 ».

2 fois 6 =12

13

2 fois 7 = 14

Donc nous avons l' encadrement : 2 fois 6 < 13 < 2 fois 7

Ensuite : nous pouvons conclure que pour diviser 13 par 2 , on prendra 2 fois 6