Pré requis:

Lecture : les unités	�
Lecture : La numération dans N	�
Lecture : Notions de grandeur , de « numération et de nombre	�
Nomenclature sur les chiffres et les nombres	�
Informations *sur N**	�
Lire : relations d’ordre avec les entiers naturels .	24

ENVIRONNEMENT du dossier :

Index warmaths

Objectif précédent: 1°)Classe des unités simples 2°) classe des mille. 3°) classe des millions et plus.

Dossier N°

Objectif suivant :1°) addition dans N 2°) classification des nombres entiers 3°)Info sur la numération des nombres décimaux 4° ) Les nombres entiers   « numération  romaine » 5°) Numération des nombres décimaux

1°)Tableau 14 2°) liste des activités dans N 3°) les N en primaires.( travaux et rappels de cours)

DOSSIER : LA NUMERATION des nombres entiers naturels ; « N » (avec chiffres arabes)

1. Définition « numération et classification » des nombres entiers.

2. Le système de numération décimal .

· A ) Les chiffres sont regroupés dans des classes :

· B) Les 4 premières classes des nombres entiers.

3. Le tableau de numération des nombres entiers naturels

4. La numération écrite.

TEST	COURS	Devoir Contrôle	Devoir évaluation	2°) situations problèmes 3°) autres séries 4°) Fiche d’exercices.	Corrigé Contrôle	Corrigé évaluation
				Les grands nombres.
				1°) Interdisciplinarité
				3°) autres séries
				4°) Fiche d’exercices.

Aller vers : Numération romaine	15

Info rappels : ne pas confondre

NOMBRE : un nombre est un alignement horizontal de chiffres. ( il est composé de un ou plusieurs chiffres)

GRANDEUR : on appelle « grandeur » un nombre associé à une unité.

UNITE  : l’unité est l’un des « objets » que l’on compte

UNITE : une unité a pour valeur « 1 » , elle n' a pas de nom en mathématique.

On ne peut mettre ensemble dans les calculs que des unités de même espèce

(En sciences on parle d 'unités de mesure de longueur (son nom est le mètre , son symbole est " m " )

* une unité vaut " 1" ; plusieurs unités de même nom (additionner) s 'appelle "une grandeur"

( exemple : 1m + 1m + 3m + 0,81 m = 4,81 m ; 4,81m est une grandeur )

des boites ; des moutons ; des mètres linéaire ; des élèves ; voitures ; des kilogrammes ;des mètres carrés ; des mètres cubes ; des litres ;…)

Vu en classe de 6^ème. (cliquez ici : info ++++)

LES NOMBRES ENTIERS NATURELS

Tu as appris à compter à l'école élémentaire, c'est-à-dire que tu sais réciter dans l'ordre, la suite naturelle des nombres entiers naturels.

0, 1, 2, 3, 4, 5, 6, 7, 8

Chaque nombre entier naturel a un suivant.

Par exemple, 13 a pour suivant 14. 157 a pour suivant _ 158_

On dit que 13 et 14 (par exemple) sont des nombres entiers naturels consécutifs.

~ Dans cette suite, existe-t-il un nombre qui sera le dernier ? _ non _ _ on dit alors que cette suite est illimitée.

on dit aussi qu'il existe une infinité de nombres entiers naturels.

* Au lieu de dire "un nombre entier naturel", on dit souvent "un entier".

COURS

1°) LA NUMERATION :
	Définition : La numération est la partie de l’arithmétique qui apprend à « former » , « à nommer » et « à écrire » les nombres. - La numération d’un nombre ( exemple « cinq ») n’existe parce qu’il y avait « quatre  » , en effet on part de « 4 », on ajouter « 1 » , pour poser l’opération « 4 + 1 » , pour obtenir « 5 » , « 5 » est un nombre , c’est aussi une valeur arithmétique., parce qu’il doit son existence au fait qu’il y avait « 4 » et qu’avec une loi de l’arithmétique on a construit (inventer) le nombre « 5 ». - La numération d’un nombre ( exemple « treize ») n’existe parce qu’il y avait « douze » , en effet il faut d’abord avoir 12 éléments, en ajouter « 1 » , pour poser l’opération 12 + 1 est obtenir le nombre immédiatement supérieur qui est « 13 » Rappels : par définition : La numération est l’ensemble des règles qui permettent de nommer et d’écrire tous les nombres avec un minimum de mots et de signes (symboles graphiques) Pour se servir utilement des nombres , il a fallu les énoncer et les représenter C’est ce qui a donné lieu a la numération parlée et à la numération écrite .
	Classification des nombres entiers naturels Le système de classement des nombres utilise le système de "rangement" en base 10 : C’est à dire :on regroupe 9 éléments(billes) plus 1 élément (bille) nous obtenons un ensemble de « 1 » ensemble d’éléments plus 0 élément seul (isolé): on écrit alors le nombre : « un et zéro » ce qui se traduit par 10 que l’on lit « dix » (ce qui donne l’ opération : 9+1 qui donne l ‘égalité ( = ) 1 0 ) Ce qu’il faut savoir sur les nombres entiers naturels Symbole : N
2°) Le système de numération décimal .
	Il n’est pas pensable d’employer autant de mots ou de chiffes qu ‘ il y a de nombres. On a donc cherché à les combiner entre eux afin de les réduire le plus possible . Il a été imaginé une vingtaine de mots qui permettent de désigner toutes les quantités. La numération parlée apprend à nommer les nombres. Numération décimale : La numération décimale consiste à réunir les unités en groupes ou collections se contenant de dix en dix . On a réuni les « quantités » en « paquets » de dix en dix fois plus grande : dix (10) ; dix paquets de dix (100) ; dix paquets de dix en paquets de dix (1000) ;....
	A ) Les chiffres sont regroupés dans des classes :
	Et chaque classe peut contenir 3 chiffres , elle est divisée en « 3 ordres » a) Unités : On a donné un nom au dix premiers nombres : ( 1^er ordre) un ; deux ; trois ; quatre ; cinq ; six ; sept ; huit ; neuf ; dix . remarque : « zéro » est un chiffre ; axiome du premier élément :l’ensemble « N » a un élément plus petit que tous les autres, on le nomme « un » et on le représente par « 1 »(Lucienne Félix ; exposé moderne des mathématique ;1962.) b ) Dizaines : On a ensuite associé ces nombres à la dizaine pour obtenir : une collection de dix unités forme une dizaine ou une unité du 2^ème ordre à la première dizaine on ajoute successivement une unité  : dix et un (onze : 11 ) ; dix et deux (douze : 12 ) ; : dix et trois (treize : 13 ) ; dix et quatre (quatorze : 14 ) dix et cinq (quinze : 15 ) dix et six ( seize : 16 ) ;dix et sept ( dix-sept :17 ) ; dix et huit (dix-huit :18 ) ; dix et neuf (dix neuf : 19) ; dix et dix , on obtient deux dizaines ou « vingt » ( 20) . C ‘est ainsi que l’on obtient la seconde dizaine à laquelle on ajoute ,de même, chacun des dix premiers nombres pour obtenir : vingt et un ; vingt et deux (vingt - deux) ; vingt et trois (vingt - trois ) ; vingt et quatre (vingt - quatre) ; vingt et cinq (vingt - cinq) ; vingt et six (vingt-six) ; vingt et sept ( vingt - sept ) ; vingt et huit (vingt-huit) ; vingt et neuf (vingt-neuf) ; vingt et dix ; on obtient la troisième dizaine ou « trente » ; ; quatre dizaines ou quarante ; cinq dizaines ou cinquante ;six dizaines ou soixante ;sept dizaines ou soixante - dix ; huit dizaines ou quatre vingt ; neuf dizaines ou quatre vingt dix ; En faisant suivre successivement les noms de chacune des neufs dizaines des neufs premiers nombres , on dénomme tous les nombres de dix à quatre – vingt – dix – neuf . c °) Centaines : une collection de dix dizaines ou de cent unités forme une centaine ou « une unité du «  3^ème ordre » . les neuf centaines sont : une centaines ou cent ; deux centaines ou deux cents ; trois centaines ou trois cents ; quatre centaines ou quatre cents ; cinq centaines ou cinq cent ; six centaines ou six cents ; sept centaines ou sept cents ; huit centaines ou huit cents neuf centaines ou neuf cents ; en faisant suivre successivement le nom de chacune des neufs centaines des noms des quatre – vingt – dix – neuf premiers nombres , on dénomme tous les nombres de cent à neuf cent quatre – vingt – dix – neuf . On a : cent un ; cent deux ; …… ;cent quatre – vingt – dix – neuf  deux cents un ; deux cents deux ; …… ; deux cents quatre – vingt – dix – neuf  ……………………….. ;…………………………………. ;………………. Neuf cents un ; neuf cents deux ; ……………… ;neuf cents quatre – vingt – dix – neuf
	B ) Les 4 premières classes des nombres entiers : sont la classe des unités ; la classe des mille ; la classes des millions ; la classe de milliards ;
	a) La Classe des unités simples : 0 à 999: Les nombres de « un » à « neuf cent quatre – vingt – dix – neuf » compose la 1^re classe des unités , dit aussi : classe des unités simples. Cette classe comprend des « unités » ; des « dizaines »et des «centaines ». après neuf cent quatre – vingt – dix – neuf  vient le nombre « mille »   ( de 0 à 999) on nomme 1^er ordre : les unités d’unité ; 2^ème ordre : les dizaines d’unités ; 3^ème ordre : les centaines d’unités.
	b) La classe des mille : 1 000 à 9999.
	nota : Mille : une collection de dix centaines forme un « mille » ou « unité du 4^ème ordre » es mille composent la seconde classe d’unités , la classe des mille qui a , comme la classe des unités simples , ses unités , ses dizaines et ses centaines . On compte de un mille à neuf cent quatre – vingt – dix – neuf  mille , comme on compte de une unité à neuf cent quatre – vingt – dix – neuf  unités. On a : un mille ; deux mille ; trois mille ;…….. neuf cent quatre – vingt – dix – neuf mille . En faisant suivre successivement le nom de chaque mille des noms des neuf cent quatre – vingt – dix – neuf  premiers nombres , on forme tous les nombres de mille à neuf cent quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf  On a : - Mille un ;mille deux ; … mille neuf cent quatre – vingt – dix – neuf . - Deux mille un ;deux mille deux ; … ;deux mille neuf cent quatre – vingt – dix – neuf  …………………………………………. - Quatre – vingt – dix – neuf  mille un ; cent quatre – vingt – dix – neuf  mille deux ; …………….. quatre – vingt – dix – neuf  mille cent quatre – vingt – dix – neuf  . - Les dizaines de mille sont les unités de 5^ème ordre (dix mille ; dix mille un ; …… dix mille neuf cent quatre – vingt – dix – neuf ; .. ; quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf ), les centaines de mille sont les unités de 6^ème ordre (de neuf cent quatre – vingt – dix – neuf  mille un ; …… jusque neuf cent quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf ). -
	c ) La classe des millions . 1 000 000 à 999 999 999Les millions composent la 3^ème classe . - «  Million » : après neuf cent quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf  vient le nombre mille mille ou « million » , ou unité du 7^ème ordre. - Vient ensuite le 8^ème ordre ( les dizaines de millions) ; puis le 9éme ordre (les centaines de millions) - On compte de un million à neuf cent quatre – vingt – dix – neuf  millions comme on compte de un mille à neuf cent quatre – vingt – dix – neuf mille et de une unité à neuf cent quatre – vingt – dix – neuf  unités . Et en faisant suivre successivement le nom de chaque million des neuf cent quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf  premiers nombres , on dénomme les nombres de un million à neuf cent quatre – vingt – dix – neuf  millions neuf cent quatre – vingt – dix – neuf  mille neuf cent quatre – vingt – dix – neuf .
	d ) Million ou milliard . Après ce dernier nombre , vient le nombre mille millions , ou billion , ou milliard , ou « unité du 10^ème ordre » les milliards composent la 4^ème classe d’unités , la classe des milliards , comme les classes précédentes , a ses unités , ses dizaines et ses centaines . On compte les milliards comme on compte les millions . Les nombres dont on peut avoir besoin dans les calculs ordinaires dépassent rarement les milliards . ( elle contient 3 ordres : le 10^ème; 11^ème et 12éme ordre…) e ) Trillion . On forme ensuite la classe des trillions , et ainsi de suite .............
3) TABLEAU de numération des nombres entiers naturels.
	On peut ainsi résumé ce qui est écrit précédemment et retenir le tableau suivant !!

4^ème Classe des milliards(billions)			3^ème classe des millions			2^ème classe des milles			1^ère classe des unités simples
centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités
12^ième ordre			9^ième ordre			6^ième ordre					1^er ordre

CONCLUSION : La théorie de la numération décimale parlée repose sur les principes suivants :

1°) Dix unités d’un ordre quelconque font une unité de l’ordre immédiatement supérieur.

2°) Dans un nombre , il ne peut y avoir plus de neuf unités de chaque ordre .

3°) Les ordres d’unités sont : les unités , les dizaines et les centaines .

4°)l’ensemble des trois ordres d’unités constitue une classe .

5°)Il suffit pour dénommer tous les nombres , jusqu’aux trillions compris , de donner un nom particulier à chacune des neufs unités composant un ordre , à chacun des deux ordres supérieurs d’une classe ; et à chacune des classes . En tout quinze mots distincts.

Remarque : l’usage a un peu compliqué cette nomenclature en changeant quelques – unes des expressions d’origine . Exemple : onze , au lieu de dix -un , etc vingt au lieu de deux dizaines , etc. Onze nouveaux mots ont été ainsi ajoutés aux quinze mots précités ; ce qui fait vingt - six mots différents pour nommer tous les nombres jusqu’aux trillions .

Pour représenter tous les nombres entiers on se sert des dix chiffres :

0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9

Enumération des chiffres :

(dans l’ordre croissant)

zéro , un , deux , trois , quatre, cinq , six , sept , huit , neuf

Notre numération est dite « décimale » .

ainsi les nombres à un 1 chiffre appartiennent à la 1^ère classe des unités d ’ unités.

ainsi les nombres à un 2 chiffres appartiennent à la 1^ère classe des unités. De dizaines

ainsi les nombres à un 3 chiffres appartiennent à la 1^ère classe des unités. De centaines

ainsi les nombres à un 4 chiffres appartiennent à la 2 ^ère classe des unités de mille

ainsi les nombres à un 5 chiffres appartiennent à la 2^ère classe des dizaines de mille.

ainsi les nombres à un 6 chiffres appartiennent à la 2^ère classe des centaines de mille.

Rappel : sur la NUMERATION des unités simples des dizaines et des centaines :

La numération apprend à former les nombres , à les nommer , à les écrire et à les lire

Les neuf premiers nombres sont appelés : les « unités simples »

Ils forment le premier ordre , on les écrit au premier rang.

Les dizaines forment le deuxième « ordre » , on les écrit au deuxième rang.

Les centaines forment les unités du troisième ordre ; on les écrit au troisième rang ;

Les unités simples , les dizaines et les centaines forment la classe des unités ou le première classe des unités d’unités simples .

TABLEAU de numération des nombres entiers naturels

D’où le tableau complet !!!!...........

4^ème Classe des milliards(billions)			3^ème classe des millions			2^ème classe des milles			1^ère classe des unités simples
centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités
12^ième ordre			9^ième ordre			6^ième ordre					1^er ordre

Immédiatement après les centaines d’unités simples viennent les « mille »

On compte par « mille » comme on compte par unités ; par dizaines et par centaines . Il y a donc des « unités de  mille » , des « dizaines de mille » et des « centaines de mille » qui forment la deuxième classe ou la classe des mille .

Notre numération est décimale , c’est à dire, qu’une unité d’ordre quelconque vaut dix unités de l’ordre immédiatement inférieur.

A savoir : Le tableau contient des "classes" : les principales classes sont :

La classe des unités simples ; la classe des mille ; la classe des millions ; …

Chaque classe contient 3 ordres d'unités qui sont l ' ordre : d'unités ; de dizaines ; de centaines .

remarques : Dans le tableau , chaque nombre entier à un suivant ; au lieu de dire « nombre entier naturel » on dira «entier ».

Lecture et utilisation du tableau :

par convention :

Les traits verticaux déterminent des « colonnes »,entre deux traits verticaux nous avons une colonne.

les traits horizontaux déterminent des lignes ; entre deux traits horizontaux nous avons une ligne.

Les "Ordres":

Chaque chiffre d ' un nombre du système décimal appartient à un ordre précis.

Un "ordre" représente une unité de numération.

Par convention :

Tout chiffre placé à la gauche d’un autre représente des unités dix fois plus grandes que celles de cet autre ; en d’autres termes, il représente des unités de l’ordre immédiatement supérieur.

Si l ’ on écrit , 93 285 , le chiffre 5 désigne des unités ; 8 des dizaines ; 2 des centaines , ect .....c’est à dire que placé au premier rang ,un chiffre désigne des unités d 'unité du 1^er ordre ; au deuxième rang ,des unités de dizaines du 2^ième ordre , au 3^ième rang , des unités de centaines du 3^ième ordre, ainsi de suite.

L’ alignement horizontal des chiffres : 18403850739 rangé dans le tableau suivant :

Classe des milliards			classe des millions			classe des milles			classe des unités
centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités	centaines	dizaines	unités
12^ième ordre	11^ième ordre	10^ième ordre	9^ième ordre	8^ième ordre	7^ième ordre	6^ième ordre	5^ième ordre	4^ième ordre	3^ième ordre	2^ième ordre	1^er ordre
	1	8	4	0	3	8	5	0	7	3	9

devient le nombre entier : 18 403 350 739 (remarquer l’espace entre chaque classe),et il se lit : dix huit milliards quatre cent trois millions huit cent cinquante mille sept cent trente neuf .

A propos des "classes"

4^ième Classe Milliards ou billons

3^ième Classe Millions

2^ième Classe Mille

1^ière Classe Unités

Chaque Classe est divisée en 3 catégories appelé « ordre » ( unité , dizaine , centaines )

Ce qui donne le tableau ci dessous :

4 ) LA NUMERATION ECRITE :

La numération écrite apprend à écrire et à lire les nombres.

Pour écrire tous les nombres , on emploie 10 symboles ou caractères ou chiffres :

1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; et le zéro « 0 » qui sert à remplacer les ordres d’unités manquant .

Numération décimale . Chiffres .

De même qu’on donne un nom particulier à chacun des neufs premiers nombres , on les représente par des caractères distincts ; ce sont :à chacun des neufs premiers nombres , on les représente par des caractères distincts ; ce sont :

1	2	3	4	5	6	7	8	9
un	Deux	trois	quatre	cinq	six	sept	huit	neuf

Ces neuf caractères ou chiffres servent à représenter de même les neufs unités composant chaque ordre.

On a : 1 dizaine ; 2 dizaines ; etc….. ; 9 dizaines

1 centaine ;2 centaines ; etc…….. ; 9 centaines.

Ecriture des nombres : l’écriture des nombres devient ainsi possible et aisé. Il suffit d’écrire successivement les unités de chaque ordre , en désignant l’ordre que ces unités représentent.

Soit à écrire le nombre six cent trente huit , on écrit : 6 centaines 3 dizaines et 8 unités.

remarque : si l’on veut se repérer par rapport à la cas centrale ; on peut déterminer la position de la case de gauche et celle de droite .

Case « Gauche »

Case  « Milieu » ou « centre »

Droite

Principe fondamental :

out chiffre placé à la gauche d’un autre représente des unités dix fois plus fortes que cet autre .on dit aussi «  représente des unités d’un ordre immédiatement supérieur à cet autre .

Dans une suite de chiffres , le premier à droite ,désigne les unités ; le second , à gauche du premier , désigne les dizaines , le troisième , les centaines , et ainsi de suite .

Le nombre six cent trente huit s’écrit : 6 3 8

Le zéro : il peut arriver que , dans un nombre , certains ordres d’unités manquent ; afin que les autres ordres puissent occuper la place qui leur convient , on remplace par un ( 0 ) zéro les ordres qui manquent.

Soit à écrire cinq mille soixante cinq ; les centaines d’unités manquent , on les remplace par un zéro , et on a 5 065

Zéro : le zéro ( 0 ) n’ a aucune valeur par lui-même , il sert à remplacer , dans l’écriture d’un nombre , les ordres d’unités qui peuvent manquer .

Chiffres significatifs : le zéro est un chiffre d’ordre ; les autres chiffres , qui ont leur valeur propre , sont appelés « chiffres significatifs ».

Ecriture d’un nombre de trois chiffres au plus :

Règle : on écrit successivement de gauche à droite les centaines , les dizaines et les unités du nombre , en ayant soin de remplacer par des zéros les ordres manquants.

Ainsi sept cent quatre s’écrit : 704

Ecriture d’un nombre de plus de trois chiffres :*

Règle : on écrit successivement de gauche à droite , et dans l’ordre où elles sont exprimées , les centaines ,les dizaines et les unités de chaque classe , en ayant soin de remplacer par des zéros les ordres manquants .

Ainsi :huit millions vingt sept mille neuf unités s’écrit : 8 027 009

Pour « écrire » en chiffres un nombre quelconque, on écrit , à partir de la gauche , chaque classe, comme si elle était seule , et l’on a soin de remplacer par des zéros les ordres d’unités qui peuvent manquer.

Lecture d’un nombre : Soit à lire 57 030 501

Les trois premiers chiffres de droite correspondent à la classe des unités ;les trois suivants à la classe des mille , les deux autres à la classe des millions . D’où ce nombre se lit : 57 millions 30 mille 501 unités.

Pour « lire » un nombre écrit en chiffres , on le partage, à partir de la droite , en tranches de trois chiffres , puis on lit et on énonce , en commençant par la gauche et en allant vers la droite ,chaque tranche comme si elle était seule , en lui donnant le nom de la classe d’unités qu’elle représente .

Valeur d’un chiffre :

Chaque chiffre a deux valeurs dans le nombre :

1°) la valeur absolue , qui est celle qu’il a par lui-même lorsqu’il est seule ;c’est la valeur de ce chiffre considéré isolément .

2°) la valeur relative , qui est celle qu’il a par le rang qu’il occupe., c’est la valeur qui donne le rang qu’il occupe dans le nombre.

Exemple : dans 724 , « 7 » a pour valeur absolue « 7 » et pour valeur relative 7 centaines ou 700.

Un nombre est égal à la somme des valeurs relatives des chiffres qui le composent . Cela résulte des principes mêmes de la numération.

On a , en effet ; 5763 = 5 mille + 7 centaines + 6 dizaines + 3 unités

Rendre un nombre entier 10 ; 100 ; 1000 fois plus grand.

Soit le nombre 17 ; si on écrit à la droite 1 ; 2 ; 3 ;..zéros , on obtient 170 ; 1700 ; 17 000 ; c’est à dire un nombre dans lequel la valeur relative de chacun des chiffres qui le composent est devenue 10 ; 100 ; 1000 ; ..fois plus grande. La somme des valeurs relatives , c’est à dire le nombre lui-même est devenu 10 ; 100 ; 1000 fois plus grande .

D’où la règle : pour rendre un nombre entier 10 ; 100 ; 1000 ; fois plus grand , il suffit d’écrire 1 ;2 ;3 ;….zéros à la droite de ce nombre .

Rendre un nombre entier , terminé par des zéros 10 ; 100 ; 1000 fois plus petit.

Si , sur la droite d’un nombre entier , on supprime 1 ; 2 ; 3 ;…zéros , on obtient un nombre dans lequel la valeur relative de chacun des chiffres est devenue 10 ; 100 ; 1000 fois plus petite . La somme des valeurs relatives, c’est à dire le nombre lui-même , est devenu 10 ; 100 ; 1000 ; … fois plus petit . D’où

Règle : pour rendre un nombre entier terminé par des zéros 10 ; 100 ; 1000 ;..etc. fois plus petit , il suffit de supprimer sur la droite de ce nombre 1 ; 2 ; 3 ; etc. ;zéros.

Pour remplir un chèque (le prix est un prix entier )

Dont sont exclus les centimes

Conseil si vous devez remplir un chèque :

Vous écrivez la partie entière en lettres suivi des mots "francs et " et la partie décimale ( après la virgule ) avec des chiffres suivi du mot " centimes"

Exemple: 230,51 €

On peut écrire:

Deux cents trente Euros et 51 centimes

Ou alors vous écrivez tout en lettres:

Deux cents trente Euros et cinquante et un centimes

A propos de l’orthographe de certains mots :

Les règles d ‘orthographe sont :

Million et milliard prennent la marque du pluriel.

Mille est invariable

exemple : 67 140 000 s’écrit soixante sept millions cent quarante mille.

Cent prend la marque du pluriel ;

Sauf : il est invariable dans certains cas particulier : il est invariable quand il correspond à une numérotation : page : trois cent ; l ' an mille trois cent)

exemple :

637 s’écrit « six cent ( s ) trente sept »  ; 600 s ’ écrit « six cent(s) »

Vingt : il en est de même que pour « cent »

Exemple :

"80" s ' écrit "quatre vingt " ;

85 s ' écrit "quatre vingt (s) cinq"

Donc , pour représenter le nombre :

« 2 mille , 3 centaines , 5 dizaines , 8 unités » il suffit d’écrire : 2 358 : le rang des chiffres indique les ordres.

TRAVAUX AUTO - FORMATIFS

CONTROLE : ( tout niveau) - ( plus facile voir « évaluation n°2 )

Qu ‘est qu ’ un nombre ?

Qu’est ce qu’une grandeur ?

A quoi sert le nombre ?

Que signifie « numération » ?

Numération orale :

Combien a t on imaginé de mots pour désigner des quantités (environ) ?

En combien a t on réuni les quantités ?

Quel est le nom donné à chacun des premiers nombres ?

Un nombre s’écrit avec des ?........................

Citer les quatre premières classes de nombres entiers :

Chaque « classe » est divisée ; en combien de parties ; précisez !

Représenter le tableau permettant de nommer un nombre !

Pourquoi dit - on que notre système de numération est « décimal » ?

Orthographe :

« Million et milliard » prennent ................................................

« Mille » est ...............................................................................

« Cent » et « vingt » ....................................................................................

(même avec une faute d’orthographe votre chèque sera « encaissé » )

EVALUATION n°1 ( classe de 6^ème )

.

A) Les positions des chiffres

a. Ecriture de position

¤ Il existe ………………… CHIFFRES : ………nommer les !

Un MOT s’écrit avec des ……………………… Un NOMBRE s’écrit avec des ………………………

Un nombre entier s'écrit avec des …………………., il ne possède pas de ………….. :

Il est la partie ……………… d’un nombre décimal

Dans une liste de nombres , on doit les séparer par le signe : ………………………….

2. Les écritures d'un nombre

a. Ecriture avec des lettres

¤ Million et Milliard sont des noms, ils prennent un « s » au pluriel.

Vingt et Cent prennent un « s » au pluriel s'ils ne sont pas suivis d'un autre nombre.

Mille est invariable, il ne prend jamais de « s » au pluriel.

Ex 3 : Ecris en lettres les nombres suivants : 600 ; 540 ; 287 ; 80 ; 1 407 ; 7 03 - 2 005 076

Compléter le tableau ci-dessous :

4^ème Classe des ………….			3^ème classe des ……………			2^ème classe des ………………..			1^ère classe des …………………..
12^ième ordre			9^ième ordre			6^ième ordre					1^er ordre
	2	8	7	5	0	3	9	1	6	3	8

Activité : Lire et écrire les nombres :
A compléter... Attention aux fautes !!!
Nombres	Ecriture (attention aux fautes )
2084
	trois milles douze unités
7280
	mille deux cents neuf unités
9021
	trente deux milles neuf cents seize
201
	neuf milles cent deus unités
1 741
	cent quatre-vingts deux
75 879
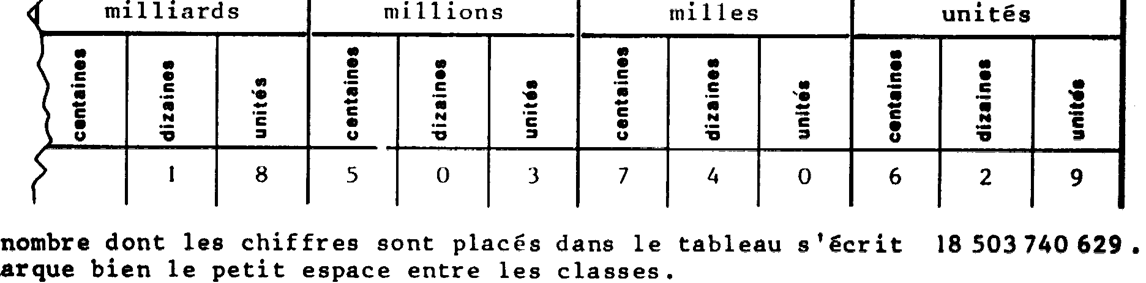
Dans le tableau ci-dessus est placé un nombre : reporté le nombre dans la case ci-dessous .	Ecrire en chiffre le nombre se trouvant dans le tableau ci-dessus ( de numération des nombres entiers)

C ) Compléter les chèques « fac-similer » ci-dessous :

.

Evaluation n°2

1°) Lire à haute voix 843 546791 71 043 4230040 500 008003 2°) Ecris avec des chiffres les nombres suivants : Quatre milliards cinq cent trente sept millions huit cent dix neuf mille treize : Deux cent vingt quatre mille dix sept : ___ ___ - ___ Vingt mille cinquante quatre Trente deux milliards onze millions cinquante mille vingt sept : - ___ NOMBRES de 1 à 100 : Combien y a - t - il de dizaines et d’unités dans ? quinze : trente : soixante - neuf : soixante dix huit : soixante seize : soixante dix huit : quatre - vingt - douze : Comment nomme - t - on un nombre composé :? de 4 unités et une dizaine : de 8 unités et une dizaine : de une unité et quatre dizaines : de trois unités et sept dizaines : de sept unités et huit dizaines : Comment nomme - t - on le nombre obtenu en réunissant ? 20 unités 1 dizaine et 9 unités 60 unités, 1 dizaine et 7 unités : Placer par ordre de grandeur croissante les nombres suivants : 80 ; 18 ; 21 ; 79 ;51 ; 49 Parmi les nombres de deux chiffres , quel est le plus grand ; quel est le plus petit ? Quels sont les nombres compris entre 30 et 40 qui contiennent plus de dizaines que d’unités ? Combien y a t - il de nombres à un chiffre et de nombres à deux chiffres ?. NOMBRES de 100 à 1 000 : Combien y a - t il de centaines , de dizaines et d’unités dans : deux cent dix sept ? Huit cent quarante huit ? cinq cent quatre - vingt ? Cent soixante douze ? cent quatre vingt treize ? neuf cent sept ? Placer par ordre croissant les nombres suivants : 501 ;178 ; 689 ; 210 ; 596 ;579 Placer par ordre décroissant les nombres suivants : 404 ; 98 ; 289 ; 700 ; 596 ; 579 Parmi les nombres de trois chiffres , quel est le plus grand ? quel est le plus Petit ? Placer par ordre de grandeur croissante les nombres que l’ on peut former : 1°) en associant les chiffres 1 ; 8 ; 5 2 ° en associant les chiffres 3 ; 1 ; 7 Numération suite exercices: Comment s'appelle l'unité du 2ème ordre ? du 4^ème ordre ?du 1er ordre? du 5^ème ordre ? du 7 ^èmeordre ? Un nombre est formé de 3 mille et 7 dizaines ; combien contient - il d ' unités ? Combien en contiendrait - il s 'il était formé de 7 dizaines de mille et de 5centaines ? Quel est le nombre formé avec trente centaines et neuf unités? avec 6mille et 70 dizaines ; 27 dizaines de mille ; 15 mille et 15 dizaines. Quel est le plus grand nombre de 4 chiffres ? de 6 chiffres? Quel est le plus petit nombre de 5 chiffres ? de 7 chiffres ? Combien doit - on écrire de zéros à la droite du chiffre 1 , si l'on veut représenter : une dizaine? un mille ? Une dizaine de millions ? une centaine de mille ? Nommer les ordres d ' unités qui contient un nombre de 5 chiffres ; de 8 chiffres . Quel est le nombre qui suit : 479 : 899 : 3 099: 8 009 : 11 099: Quel est le nombre qui précède : 10 000: 10 100 20 020: 21 000 : 100 100 : 101 000 :