Réduction au même dénominateur :
Ci-dessous :
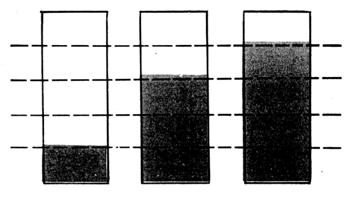
Observons l’ éprouvette que l’on remplit successivement ;
Les
éprouvettes sont graduées « également » en 5 parties égales. Une
éprouvette peut être remplie aux
![]()
A) Les fractions ont le même dénominateur :
|
La première est remplie au |
|
|
|
On
remarque que : Lorsque
deux fractions ont le même dénominateur , la plus grande est celle qui a le
plus grand numérateur. |
B ) Autre
exemple : les fractions ont des dénominateurs différents :
On veut comparer :
![]()
|
On divise une bande en 3
parties égales., on en prend 2 parties
sur 3 soit les |
|
|
|
|
|
|
|
On divise la même bande
en 4 parties égales on en prend 3 parties
sur 4 soit la fraction : |
|
|
|
|
|
|
|
|
|
|
Pour comparer les fractions 2/3 et
3/4 , on remplace par des fractions égales ayant le même dénominateur :
1 . Classer chaque série de fractions de la plus
petite à la plus grande.
![]()
2. Réduire au même
dénominateur , et comparer :
![]()
![]()
![]()
On en conclut que : il faut simplifier les fractions , quand
cela est
possible, AVANT de chercher aux
(deux) fractions un même dénominateur . ( on dit aussi que l’on
cherche le dénominateur commun.)
3. Simplifier, puis réduire
au même dénominateur.
![]()
4. Simplifier , si cela est possible , puis
réduire au même dénominateur.
![]()
Examiner les fractions 7 / 9
et 5/6 , on leur trouve pour
dénominateur commun , par le moyen habituel ; mais « 18 » est un dénominateur commun ,
plus petit que « 54 » ;
![]()
5 . Réduire les fractions suivantes au
dénominateur commun indiqué :
![]()
6. Réduisez les fractions suivantes au même
dénominateur le plus petit possible (c’est parfois un des dénominateurs)
![]()
7. Simplifiez, puis réduisez au même
dénominateur, le plus petit possible
![]()
8. On peut réduire au même dénominateur plusieurs fractions, on
multipliant les deux termes de chacune d’elles par les dénominateurs des autres
(après simplification s’il y a lieu). Ainsi pour
![]()
Réduire ainsi :
![]()
9. Combien
de minutes font:
|
|
|
|
|
Classez ces 4 fractions de la plus petite à la plus
grande : a) selon les résultats
obtenus; b) en les exprimant on soixantièmes
d’heure.
10. Une station d’essence comporte 2 citernes de chacune
a) on
comparant les deux fractions;
b) on
comparant leurs valeurs décimales;
c) on
calculant ce que chacune contient, en litres.
11. Les rectangles ci-dessous sont égaux. Reproduisez-les.
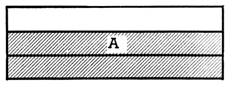
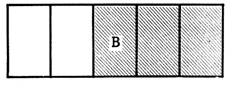
Quelle fraction de chacun d’eux est coloriée?
Pour comparer ces surfaces,
reportez sur chaque rectangle les parallèles de l’autre : en combien de parties égales chaque rectangle est-il alors
divisé? Comptez, dans chacun, les
parties coloriées ;exprimez-en le nombre en fraction du rectangle : quelle est la plus grande surface coloriée ?
12. Les terres ensemencées d’une ferme ont une
surface de
a) Sans
calculer les surfaces ensemencées, dites quelle est la plus grande : celle du
blé ou colle des autres céréales?
b) Vérifiez on calculant Ces surfaces,
c) Quelle est la surface consacrée aux plantes
sarclées ? Quelle fraction de la surface totale représente-t-elle ?
Simplifiez-la.
13. Une camionnette pesant

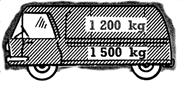
a) Combien
pèse, pleine, la camionnette ? la fourgonnette ?
b) Quelle fraction du poids on charge représente la
charge utile de chaque véhicule ? Simplifiez et comparez ces fractions.
c) Lequel,
des deux véhicules, a le meilleur rendement ?