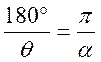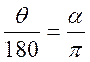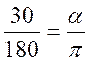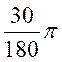Les angles orientés

Pré requis:

Les unités de mesure d’angles

 

 

 

Position d’un point

3D Diamond

 

 

Les vecteurs

3D Diamond

 

 

ENVIRONNEMENT du dossier:

 

Index  warmaths

Objectif précédent :

Le radian  Sphère metallique

Objectif suivant :

Extension « arc et angle » en trigonométrie.

Retour à la liste des objectifs de formation

 

 

 

 

DOSSIER : les ANGLES ORIENTES.

-       I) Mesure d’un angle en radian.

-       II ) Détermination de la mesure  principale d’un angle orienté.

-        

TEST

 Filescrosoft Officeverte

COURS

                FilesOfficeverte

Devoir  Contrôle FilesOfficeverte

Devoir évaluation FilesOfficeverte

Interdisciplinarité

                        Filescrosoft Officeverte

 

Corrigé Contrôle  FilesOfficeverte

Corrigé évaluation  FilesOfficeverte

 

 

COURS

 

Mesure d’un angle en radian

Pré requis Boule verte

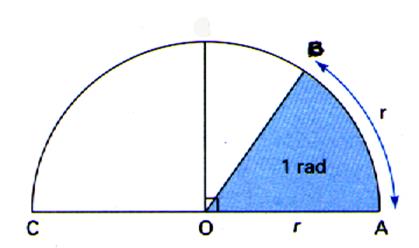
Un angle de 1 radian est un angle au centre qui intercepte un arc de cercle de longueur « r » sur un cercle de rayon « r ».

Info :

-L’angle plat a pour mesure 180°

-       la longueur de l’arc AC est pr ;

-       on en déduit que la mesure de l’angle plat en radian est donc : « pi »

-        

c26

Si l’on désigne par q la mesure en degré et a la mesure en radians d’un même angle.

On peut écrire :   nous sommes en présence d’une proportionnalité. (voir le tableau de proportionnalité ) d’où :

 

 

II ) Détermination de la mesure  principale d’un angle orienté :

 

Se souvenir que l’unité d’angle sera le radian , le deuxième support est le cercle trigonométrique . (c’est un cercle orienté de rayon 1. Dont un point se déplace sur sa circonférence  dans le sens + s’il tourne dans le sens inverse des aiguilles d’une montre)

                

 


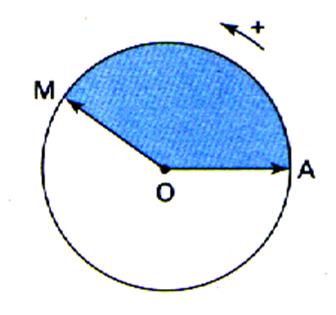
 Nous plaçons deux points « A » et « M » sur le cercle .nous obtenons deux vecteurs      et   OM      ayant même origine « O » . ;

 

 


ces deux vecteurs forment l’angle orienté  noté  ( OA ; OM )

 

 

La mesure principale d’un angle orienté est un nombre appartenant à l’intervalle ] -p ;p ].

 

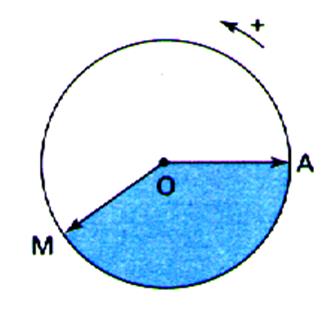
Exemples :considérons le déplacement du point « A » vers  «M »

 

Le déplacement de A s’effectue dans le sens positif.

On pourrait dire que si « A » se déplace vers « M » par le plus court chemin.

     L’aire « bleue » représente :          a = +  

c25

Le déplacement de A s’effectuera dans le sens négatif.

               « A » se déplace vers « M » par le plus court chemin.

     L’aire « bleue » représente :          a = -

c24

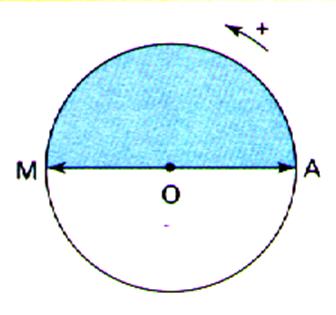
Cas particulier : A et M sont diamétralement opposés.

a = p

c23

 

 

 

 

 

 

TRAVAUX AUTO _ FORMATIFS

 

 

CONTROLE:

 

Donner les caractéristiques d’un angle orienté.

 

 

EVALUATION:

 

Calculs

 

Donner en fonction de « pi » la mesure des angles suivants : 30° ;45°,60°,90°,120°,135° à partir de la relation.

 

 Si l’on désigne par q la mesure en degré et a la mesure en radians d’un même angle.

 

 

Calculer en degrés la mesure des angles suivants : 1 rad ; rad ;rad

 

 

 

 

 

 

Interdisciplinarité

Problème  1

 

Un avion a parcouru 250 km suivante la demi-droite ( O t ) , Quelle est sa position dans le repère (  ) ?

c21

 

 

Problème  2

 

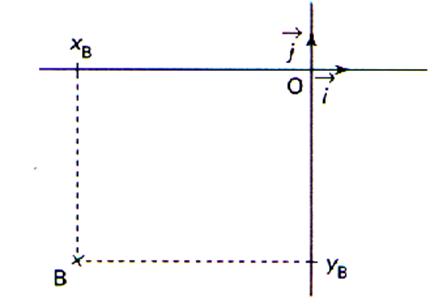
Un navire a déclenché sa balise de détresse qui nous fournit sa position. Il est situé en B dans le repère (  ) , à quelle distance se trouve – t- il ?

Quelle direction doit-on suivre pour le secourir ?

c22

 

 

 

 

 

 

Calculs   corrigé.

 

Donner en fonction de « pi » la mesure des angles suivants : 30° ;45°,60°,90°,120°,135° à partir de la relation Si l’on désigne par q la mesure en degré et a la mesure en radians d’un même angle.

 Pour 30° : ; a == rad

 

 

                    

Calculer en degrés la mesure des angles suivants : 1 rad ; rad ;rad

180° ; 72° ;60°

 

 

/body>