Pré requis:

Les unités de mesure d’angles
Les secteurs circulaires
Les secteurs angulaires
Position d’un point
Les vecteurs

ENVIRONNEMENT du dossier:

Index warmaths.	Objectif précédent :   Le radian   Les angles orientés	Objectif suivant : Le cercle trigonométrique Direction : les fonctions circulaires…	Retour à la liste des objectifs de formation

DOSSIER : Extension de la notion  d’ arc et angle.

Chapitre 1 :

I) Unité d’arc.

II ) Unité d’angle– unités correspondantes.

  Voir : Changements d’unité.

Chapitre 2 :

III) Cercle orienté

IV) Arc orienté. ( sa mesure algébrique)

V) Arc généralisé. Arc trigonométrique.

VI) Mesure algébrique de tous les arcs trigonométriques AB

VII) Théorème.

VIII) Formules de Chasles pour les arcs.

Chapitre 3 : Angle

I) Plan orienté

II) Angle orienté et sa mesure algébrique.

III)Angle généralisé et angle trigonométrique.

IV ) Angle au centre et arc intercepté.

V )  Les 2 conséquences.

Dont la Formule de Chasles pour les angles

 

 

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

 

 

COURS

 

Chapitre 1 :

 

I) Unité d’arc.

En trigonométrie on prend généralement pour unité l’arc de 1 radian, dont la longueur est égale au rayon.

Le cercle entier, qui a pour longueur 2 π  R , à pour mesure  2 π radians.

Le demi cercle a pour longueur (2 π / 2)   soit  π radians  ( = 2 quadrants = 180° ,= 200 gr)   .

 

Sur un cercle de rayon R ,un arc de   radians à pour longueur  R

 

II ) Unité d’angle– unités correspondantes.

 

L’angle de 1 radian est l’angle qui, dans la position d’angle au centre,intercepte un arc de 1 radian.

Un angle plat mesure π radians , un angle droit  radians.

Plus généralement,on appelle « unités correspondantes » celles qui se correspondent par angle au centre et arc intercepté, par exemple degré -angle (au centre)et degré arc (intercepté).

 

Voir : Changements d’unité.

Ils découlent  de la règle fondamentale : le rapport de deux grandeurs est égal au rapport des nombres qui les mesurent avec la même unité,d’où, en appelant « r » , « d », « g » les mesures d’un arc en radians, en degrés et en grades :

 

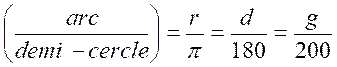
Voici quelques changement d’unités usuels :

 

Radians (arcs ou angles)	2 π	π
Valent :	360°	180°	90°	60°	45°	30°
	400 gr	200 gr	100 gr	(200/3)  gr	50 gr	(100/3) gr

 

 

Chapitre 2 :  ARCS.

 

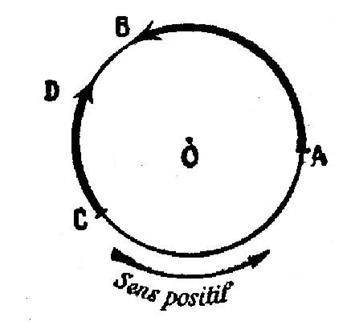
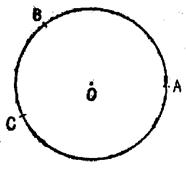
III) Cercle orienté :

Un cercle orienté est un cercle sur lequel on a choisi un sens de parcours comme sens positif ; le sens contraire s’appelle « sens négatif ».

 

IV) Arc orienté. ( sa mesure algébrique)

 

On appelle « arc orienté » un arc sur lequel on a choisi un sens. Si c’est de A vers B ; « A » s’appelle « origine »  et « B » l’extrémité.

On écrit    , qui se lit :arc orienté AB.  ( la flèche est courbe)

 

Le cercle qui porte l’arc étant orienté et une unité d’arc étant choisie, on appelle « mesure algébrique » d’un arc orienté AB le nombre ayant :

1°) comme valeur absolue : la mesure de l’arc géométrique AB ;

2°)Pour signe ,

     + si l’arc a le sens positif du cercle ;

-   s’il a le sens négatif du cercle.

On représente cette mesure par AB surmonté d’un arc (qui se lit : AB algébrique)

 

. En degrés , la mesure algébrique d’un arc est comprise entre  - 360 °  et + 360°

  En radians , la mesure est comprise entre  - 2 π  et  +2π.

 

Arc généralisé – Arc trigonométrique.

 

Arc généralisé :

Imaginons un point « M », mobile sur un cercle,partant d’un point « A » dans un sens quelconque,mais invariable une fois choisi,et pouvant, dans ce mouvement, franchir le point « A » un nombre quelconque de fois. Quand ce mobile « M » s’arrête en un point « B » ,on dit qu’il a parcouru un « arc généralisé ».

 

Représentation concrète d’un arc  généralisé .  Un fil enroulé plusieurs fois sur un disque circulaire donne un représentation concrète d’un tel arc.

 

    Arc trigonométrique :

On appelle « arc trigonométrique » un arc généralisé orienté.

La mesure d’un arc trigonométrique est un nombre algébrique quelconque.

Exemples :

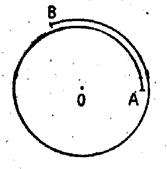
	L’arc AB = (360°+120°)  = + 480°
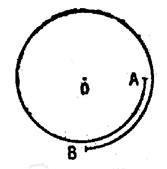
	L’arc AB = (-360°- 90°)  = - 450°
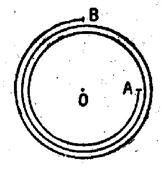
	L’arc AB = (- 720°-270°)  = - 990°

 

Mesure algébrique de tous les arcs trigonométriques AB

 

Soit « a » la mesure , en radians, de l’arc géométrique positif AB (inférieur à un cercle) soit 2 pi.

 

1°) Imaginons un mobile partant de « A » dans le sens positif ;

la 1^ère fois qu’il arrive en « B » la mesure algébrique de l’  arc parcouru est « a » ;

la 2^ème fois, la mesure algébrique  est « a + 2 π »               ( « a » + 1 cercle)

la 3^ème fois elle est de « a + 2 (2 π) »                        ( a + 2 cercles)

la 4^ème fois, elle set de  «  a + 3 (2 π) »   ,………………et ainsi de suite.

 

2°) Supposons maintenant que le mobile parte de « A » dans le sens négatif ;

la 1^ère fois qu’il arrive en « B » , il a parcouru le cercle entier moins l’arc « a », ,c'est-à-dire un arc géométrique « 2π – a » ,dont la mesure algébrique est «  -  (2π – a) »  ou  «  a –2π » ;

la 2^ème fois qu’il arrive en « B » , il a parcouru 2 cercles entier moins l’arc  « a » , c'est-à-dire un arc dont la mesure arithmétique est «  2 (2π ) – a » , et dont la mesure algébrique est – (2 (2π ) – a) =  « a – 2 (2π ) » ; 

la 3^ème fois , la mesure algébrique de l’arc parcouru est :   «  a – 3 (2 π) »

Et ainsi de suite.

 

En résumé :

Les mesures algébriques de tous les arc AB sont :

………….a – 6 π       a - 4 π      a - 2 π      a   a +2 π   a + 4 π….

 

Il en résulte  que deux quelconques d’entre elles ,  et ’ , diffère d’un multiple de 2 π ;autrement dit :  ’  =  + k 2 π

« k » étant un entier algébrique quelconque. D’où  l’énoncé du théorème.

 

Théorème : Pour que deux arcs d’origine « A » aient la même extrémité ,il faut et il suffit que leurs mesures algébriques soient liées par la formule

 

’  =  + k 2 π   radians

ou

’  =  + k (360)  degrés

Formule de Chasles pour les arcs :

Si deux arcs trigonométriques  , l’arc  AB et l’arc BC sont de même sens , leur ensemble (somme) constitue un certain arc trigonométrique AC tel que :

 

L’arc AB + l’arc BC= l’arc AC

 

Si maintenant on prend l’un quelconque des arcs AB, l’un quelconque des arcs BC et l’un quelconque des arc AC , chaque terme de l’égalité précédente varie d’un nombre entier des cercle , de sorte qu’on a :

L’arc AB + l’arc BC= l’arc AC   à  k fois 2 π  près.

 

 

Chapitre 3 : ANGLES

 

Plan orienté. :

On appelle « plan orienté » un plan sur lequel on a choisi un des deux sens possibles de rotation comme sens positif ; et le sens contraire que l’on appelle « négatif »

 

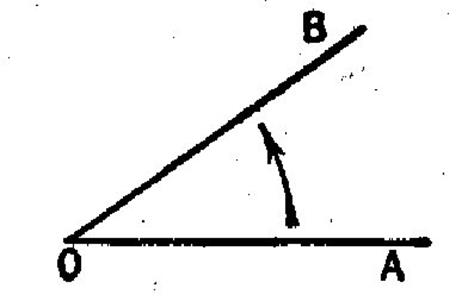
Angle orienté et Sa mesure algébrique :

 

On appelle « angle orienté » un angle balayé dans un sens déterminé. Si c’est de OA vers OB , OA s’appelle « côté origine » et OB s’appelle « côté extrémité » . On écrit    ou    Le plan qui porte l’angle étant supposé orienté,et une unité d’angle choisie,on appelle « mesure algébrique » d’un angle orienté AOB tracé dans un plan orienté le nombre algébrique ayant : 1°) pour valeur absolue la mesure de l’angle géométrique ; 2°) pour signe +  si l’angle a le sens positif du plan ; -  si l’angle a le sens négatif du plan.

Cette mesure algébrique, que l’on représente par    ou    est un nombre compris entre -2 π  et  + 2 π , en radians , ou entre  - 360° et + 360 ° , en degré.

 

 

Angle généralisé et Angle trigonométrique.

 

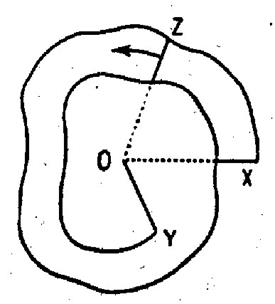
Angle généralisé : Imaginons une demi droite OZ mobile autour du point O  et une demi droite fixe OX ; OZ tourne à partir de OX dans un sens quelconque mais invariable un fois choisi,et peut,dans ce mouvement, franchir la demi-droite OX un nombre quelconque de fois. Quand elle s’arrête dans une certaine position OY , on dit qu’elle a balayé un angle généralisé ;   Un tel angle n’est pas nécessairement orienté ; nous aurions pu supposer en effet que la demi droite qui l’ a engendré soit partie de OY pour arriver sur OX.

Sur la figure on a supposé le pourtour de l’angle découpé, pour laisser vois les divers « feuillets ».

 

Angle trigonométrique :

 

On appelle « angle trigonométrique » un angle généralisé orienté . La mesure d’un angle trigonométrique est un nombre algébrique quelconque.

 

 

Angle au centre et arc intercepté.

 

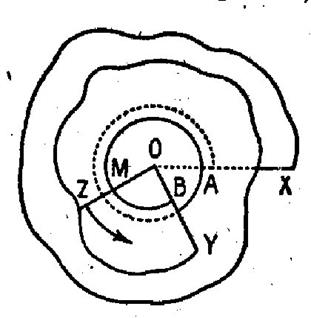
Soit M un point d’un cercle et OZ la demi droite OM . Si le point M décrit un arc trigonométrique AB, la demi droite OZ  engendre un angle trigonométrique AOB. Nous dirons encore que  est un angle au centre , et l’arc AB est l’arc intercepté.   Si on convient d’orienter le cercle et le plan dans le même sens et de prendre des unités correspondantes ( info ?), on voit aisément que «  Tout angle au centre a même mesure que l’arc intercepté ».   Et donc :   = l’arc AB

 

V) Conséquences :

 

Conséquence 1 :

Deux demi-droites OA ,OB définissent une infinité d’angles trigonométriques AOB ; les mesures algébriques  de tous ces angles sont de la forme :

 

+ k 2 π                      ( k , est un entier algébrique)

 

  étant l’une quelconque d’entre elles.

 

Conséquence 2 :

 

Formule de Chasles pour les angles :    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

TRAVAUX AUTO _ FORMATIFS

 

 

CONTROLE:

A élaborer…

 

 

EVALUATION: