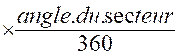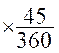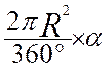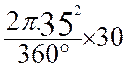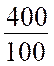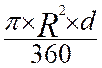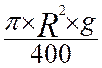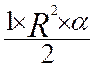Les angles « présentation »

Notion d’arc :

Le cercle

Index   warmaths

Objectif précédent :

1°)le rapporteur d'angle.

2°) Aire d’un secteur circulaire :

Objectif suivant

1°)application :  Statistique : les diagrammes circulaires

2°) Extension « arc et angle »

3°) Le cercle trigonométrique

Liste de cours sur « les angles »

DOSSIER : LES SECTEURS CIRCULAIRES et calculs de l’aire d’un secteur circulaire..

-       Représentation graphique.

-       Aire d’un secteur  circulaire . (divisé en degré) 

-       Formule : calcul de l’ aire  d’un secteur circulaire ( en fonction du degré ; du grade ou de radian)

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

COURS

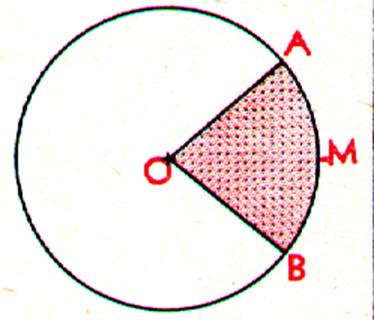
Représentation graphique du secteur circulaire

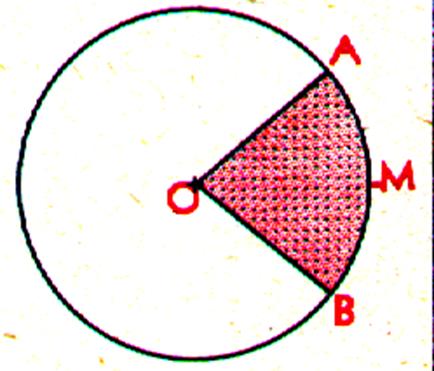
La partie  « ombrée » représente le secteur circulaire d’un disque .

AIRE D’UN  SECTEUR CIRCULAIRE

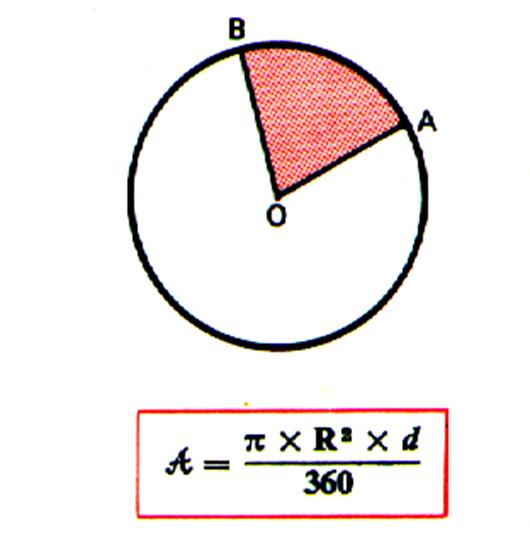
                                      On obtient l’aire d’un secteur circulaire  en multipliant l’aire du disque  par le nombre de degrés de l’arc et en divisant le produit par 360.

Secteur circulaire :

SOS ARC et angle

On appelle « secteur circulaire » l’aire comprise entre un arc et les deux rayons ( OB et OA )  qui aboutissent à ses extrémités.

Aire : on obtient l’aire d’un secteur circulaire en multipliant l’aire du disque par le nombre de degrés de l’angle du secteur et en divisant par 360.

A = p r²

Application

                      Trouver l’aire d’un secteur circulaire dont le rayon du cercle a 5 m et dont l’angle du secteur égale 45°.

1° aire du disque = 5² 3,1416 = 78,54 m²

2° aire du secteur :  78,54 =  78,54 = 9,8175 m²

Autre définition :  Segment circulaire

Info plus ++++

On appelle segment circulaire l’espace compris entre un arc et la corde qui la sous tend

Le secteur circulaire peut être ( très souvent le cas ) exprimé en degré ; ou en grade  et en radian  :

Calcul 1 : Calcul de l’aire d’un  secteur  circulaire  dont l’angle est exprimé en degrés :

Formule à utiliser        :  A  = °

Explication :   On divise l’aire du disque en 360 parties égales ; pour multiplier par le nombre degrés de l’angle au centre de l’arc.

Si l’angle alpha(  )vaut 30 ° le rayon ( OA ou OB ) 35 mm :

On sait que A = ° ;

soit : A = ° =  641,08333

soit 641 mm²

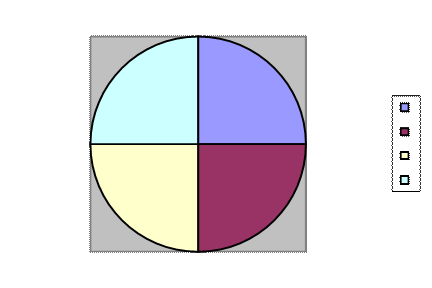
En statistique une des représentations graphiques des pourcentages est le « diagramme circulaire » .  La circonférence est divisée en 100 parties égales ;

Relation entre % et valeur en degré :

360° représente 100%   ;  soit  ;       Le 1% représente 3,6° d’angle 

Relation entre % et valeur en grade :    400 gr. représente 100%   ;  soit  ;

Le 1% représente 4 grades d’angle  .

INFO Plus ++++

Calcul d’aire d’un secteur angulaire

Rappel§§§

Suivant les unités de mesure des angles nous obtenons des « formules » différentes

Angle exprimé en « degré » ; symbole  « d » représente le nombre de degrés

A = 

Angle exprimé en « grade» ;    « g » représente le nombre de grades

A = 

Angle exprimé en « radian » ;    « a »  représente la mesure en radians du secteur angulaire.

A = 

ci-dessous : Applications des  secteurs circulaires ( arcs et aires)  utilisés en statistique .