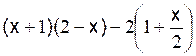Pré requis :
|
voir les définitions de bases abordées dans les
égalités EG1 et EG2 |
|
|
Collège |
|
|
Collège |
|
|
Algèbre convention d '
écriture ;… |
|
|
Il faut savoir
décomposer un nombre entier sous forme de produit. |
Objectif : Savoir factoriser et ou développer des expressions algébriques.
Environnement du
dossier:
|
Objectif
précédent : |
Objectif
suivant : |
DOSSIER « algèbre »:
FACTORISER
|
|
|
|
|
|
|
|
|
|
COURS |
Interdisciplinarité |
|
Ce cours « factoriser -
développer » ou « développer
factoriser » fait parti d’un des chapitres de la leçon qui porte sur
le « calcul littéral » en algèbre.
Ces chapitres sont entre autre : le
développement d’un produit, les équations, les égalités ; la résolution
d’équations , les problèmes en algèbres.
Approche :
Soit le nombre 15 = 3 fois
5 ; et le nombre 18 = 3 fois 6
je décide d’additionner 15
+ 18 cela revient à faire
l’addition ( 3 fois 5) + (
3 fois 6 ) que l’écrit : ( 3 x 5 )
+ ( 3 x 6 )
nota : Vocabulaire : a) les
nombres « 3 », « 5 »,
« 3», « 6 » sont appelé « facteur » . b) ( 3 x
5 ) et ( 3 x 6 ) sont appelés « terme »
Observation : le nombre « 3 »
(appelé : facteurs) existe dans les deux termes, on dira : le nombre « 3 » est le facteur
commun au deux termes ( 3 x 5 ) et ( 3 x 6 )
De
quoi se compose un facteur ? ( un « terme ») :
Un facteur peut être un nombre, une lettre, il n’est
jamais seul , il est associé au nombre ou a une autre lettre . Dans le cas ou
l’expression possède des parenthèses séparées par le signe
« virtuel » de la multiplication alors chaque parenthèse et son contenu est aussi
appelé facteur.
Exemple :
x Þ puisque
« x » peut être
multiplié par l’élément neutre « 1 » ; x = 1
fois x
donc « x » est un facteur ;
2 x Þ 2 et
« x » sont des facteurs.
( 2x ) ( x +3) Þ (2x)
et ( x +3) sont appelés
« facteurs »
Différence
entre un terme et un facteur:
les termes sont situés à droite et à gauche du signe opératoire « plus » ou « moins »,les
facteurs sont situés à droite et à
gauche du signe ( x ;
appelé « croix » qui signifie
« multiplier »).
Termes
semblables:
On appelle "termes
semblables" d'un polynôme des termes qui ne diffère que par les coefficients.
Ainsi l' expression 8a2 +3bc + 5d2
- 4a2
Est un polynôme .( 8a2 , -4 a2 sont des termes semblables.)
Vocabulaire:
Le signe
opératoire de la multiplication ,en
forme de « croix » , peut se
traduire par plusieurs
« mots »:
Par le mot
« fois » : 3 ´ 7 se lit : ( 3 fois 7)
Par le groupe de mots :«
multiplié par » : 3 ´ 7 se lit
« 3 multiplié par 7 »
Par le groupe
de mots :« fois entre parenthèses » : pour 3 (
5+2) on lit ( 3 fois entre
parenthèses « 5 + 2 »
Par : « facteur
de » pour 3 ( 5+2) on peut
lire « 3 facteur de
5+2 »
d'où la
convention d' écriture :
Dans les expressions algébriques
le signe « multiplier » n ‘ est jamais représenté.
On ne trace pas la « croix » pour éviter
toute confusion avec la lettre « x »,qui
est couramment utilisée pour
représenter « l’inconnue » .
A
savoir qu ' en l’absence de signe ,il y a toujours
« produit » entre:
►un nombre et une lettre
: 3x ;lire
« trois fois ixe »
(le mot « fois » doit être remplacé par
« multiplié par » )
►deux lettres : ab
; lire « a fois
b » ou « a » facteur
« b »
► un nombre et une racine: 3![]() ;lire « 3
fois racine carré de 18 »
;lire « 3
fois racine carré de 18 »
►º un nombre et une parenthèse
: 3 ( 2x +
1) ; lire « 3 fois entre parenthèses 2 ixe plus un » ou
aussi « 3 facteur de 2ixe plus
un »
les groupes de mots « fois
entre parenthèses » et « facteur de » ont la même signification .
►ºune lettre et une parenthèse:
x ( 2x
+2) , lire « ixe facteur
de 2ixe plus 2 »
►ºentre deux parenthèses : (2x+1)(3x+2) , lire
« 2ixe plus un » entre parenthèses facteur de « 3 ixe
plus 2 » )
NOTA : Les développements de produits types à retenir sont :
|
a ( b + c) = a b + a c |
a ( b - c ) = ab - ac |
( a + b ) ( c + d ) = ac + a d + b c + b d |
Remarque : La factorisation est le travail inverse du développement.(par le développement on peut vérifier que la factorisation est bonne)
Pré requis : On demande de développer
et puis réduire chacun des produits
suivants.
|
|
Résultat : |
|
Résultat : |
|
A = ( x + 3 ) ( x - 5) |
|
C = ( -4 x + 1) ( 2 - x) |
|
|
B = ( x + 4 ) ² |
|
D = ( x - 5 ) ² |
|
Remarque : ( x + 4 ) ² est égal
à ( x +4 ) ( x + 4)
Réponses : x² + 8x +16 ; x² - 2x - 15 ;
4x² - 9 x +2 ; x² - 10x + 25
Attention : avant de vouloir développer ; il faut savoir
« identifier » si l’expression est « développable » :
il faut
se poser la question suivante :
-
est ce que l’expression donnée est un produit ? on peut alors développer.
-
Est ce que c’est une suite de termes ? alors
on ne peut pas développer , on peut simplifier.
Expérience : Regarder les expressions suivantes, elles sont
différentes, une seule est développable ,
laquelle ? :
|
Somme
de deux termes |
Produit
de facteurs |
Différence
de deux termes |
|
A = ( x + 3 ) + ( x - 5) |
B = ( x + 3 ) ( x - 5) |
C = ( x + 3 ) - ( x - 5) |
Dans deux des cas on passe à une simplification d’écriture
SIMPLIFICATION :
Exemples de simplifications d’écriture :
La suppression de parenthèses précédées d’un signe
+ ou - est une simplification il faut se souvenir que :
( x +
5 ) = x + 5 ; + ( x +3) = x +
3 ; + ( x - 2 ) = x -2 ; + ( - x - 3) = - x - 3 ;
- ( x +
5 ) = - x - 5 ; -( x +3)
= - x - 3 ; - ( x - 2 ) = - x +2 ; - ( - x - 3) = + x + 3 ;
Simplifications d’écritures :
|
Départ |
Simplification et
on regroupe (réduit) |
Commentaire : |
|
A = ( x + 3 ) + ( x - 5) |
A = x + 3 + x
- 5 =
2x - 2 |
On supprime les parenthèses |
|
C = ( x + 3 ) - ( x - 5) |
C = x + 3 - x
+ 5 = 0x + 8 = C = 8 |
On supprime les parenthèses |
|
D = ( x - 1) - ( 2x - 3) |
D = x - 1 - 2x
+ 3 = - x +2 |
On supprime les parenthèses |
|
E = 2 ( 3 +x ) - ( 2x +1) |
E = 6 + 2x - 2x - 1 E = 0x + 5 = 5 |
On développe le premier terme , on supprime
les parenthèses. |
|
F = - 5 ( 4x - 1) + 3 ( 2x -1) |
F = - 20x + 5 + 6x -3 F = - 14 x +2 |
On développe le premier terme , on supprime
les parenthèses. |
|
G= ( 3x +1)- (5x +2) + ( 2x -3) |
G= 3x +1 - 5x -2 + 2x -3 G = 0x - 4 = -4 |
on supprime les parenthèses. |
|
H = ( x² + x +1) - (2x²- x) |
H = x² + x +1 - 2x² + x H = - x² +2x +1 |
on supprime les parenthèses. |
|
K = ( 5x² - x) - ( 2x² +3x - 1) +2 |
K = 5x² - x - 2x²-3x+1 +2 K= 3x² - 4x +3 |
on supprime les parenthèses. |
Nous avons vu pour simplifier il faut parfois développer puis
ensuite « réduire ( qui est une sorte de
factorisation) » pour « simplifier ».
Niveau + : on demande de simplifier l’écriture proposée.(on est parfois obligé de développer , pour n’avoir qu’ une suite de
termes)
|
Exercices. |
Résultat : |
Commentaire : |
|
A = 3 ( x -5) - x ( x -2) |
A = 3 x -15 - x² + 2x A= -x² + 5x - 15 |
On développe les deux termes , on supprime
les parenthèses. |
|
B= x² - 3 - (x - 1) ( x +1) |
B= x² - 3 - (x - 1) ( x +1) B = x² - 3 - ( x² -1) B = x² - 3 - x² +1 B = 0 x² -2 = -2 |
On développe le troisième terme, on supprime les parenthèses. |
|
C = - ( x +2) x + 3 ( x - 5) |
C = - ( x +2) x + 3 ( x - 5) C =- x - 2 + 3x - 15 C = 2x - 17 |
On développe le deuxième terme, on supprime les parenthèses. |
|
D = |
D = ( x + 1 ) ( 2 - x ) - 2 - x D = 2x - x² +2 - x - 2 -x D = x² +0x +0 D = x² |
On développe les deux termes, |
|
|
|
|
Le mot « factoriser » doit être associer au mot
« facteur » (voir
objectif sur l’égalité) |
|
Par définition :
« Factoriser » est une activité mathématique qui consiste à transformer une somme
( ou expression) algébrique pour la mettre sous la forme « d’un
"produit" de facteurs ».
On dit aussi que
« factoriser » c’est écrire une somme ou une différence sous
la forme d’un produit. On dit encore : écrire sous la forme d’un produit
de facteurs du premier degré.
Le facteur commun peut être :
|
Cas : |
Exemple |
Commentaire. |
|
1 - un
nombre |
T = 10a +25 T = 5 fois 2a + 5 fois 5 T = 5 ( 2a + 5) |
On applique la formule : a b + a c = a ( b + c) On met « 5 » en facteur. |
|
R = R = 5 fois 3a + 5 fois 4 R = 5 ( 3a +4) |
Remarque : on a aussi : a b - a c
= a ( b - c ) |
|
|
2 - Un
nombre et une lettre. |
T = 14 a² - T = 2 fois 7 fois « a » fois
« a » - 3 fois 7 fois « a » T = 2a (
7a) - 3 ( 7a) T = ( |
On recherche si
le produit de facteurs communs
existe :ici c’est « 7a » |
|
3 - Une
expression du type « ax+b) |
T = 5 ( x + 3) ( 3x - 4) + ( 7x -5) ( x +3 ) T = ( x + 3) [ 5 ( 3x -4) + (7x - 5) ] T = ( x + 3) [ 15 x - 20 + 7x - 5 ] T = ( x + 3 ) ( 22 x - 25 ) |
On recherche le facteur commun : ( x+3) On met (x +3) en facteur . On utilise la forme ab +ac = a ( b + c ) On développe l’intérieur des crochets . On réduit le deuxième facteur. |
La
factorisation n’est possible que si l’on identifie un « facteur commun » .
Ce
facteur est soit "évident" ou on le découvre
après avoir fait la décomposition de chaque terme de l’expression algébrique.
(La factorisation n’est pas toujours possible
ou toujours évidente si l'expression algébrique n'est pas transformée
en somme algébrique)
Procédure permettant de
factoriser « une somme »:
Exemple : factoriser 3x+15
a ) Décomposer sous forme de produit chaque terme
de l’expression:
3x = 3 fois x
15 = 3 fois 5
b ) Identifier dans les termes quel est le chaque
facteur commun ou le produit de facteurs
communs (on dit aussi de même indice).
Facteur commun =
3
c )
Sortir le facteur commun : Ecrire le facteur ou le produit de
facteurs commun ; ouvrir une parenthèse, réécrire l’expression donnée en
remplaçant dans la décomposition de chaque terme , le ou les facteurs
communs, par l’élément neutre « 1 »
puis fermer la parenthèse .
3 ( 1![]() x + 1
x + 1![]() 5)
5)
Pour chaque terme (se
trouvant dans les parenthèses ) remplacer la décomposition par un nouveau
produit.
puisque : 1![]() x = x et 1
x = x et 1![]() 5 = 5
5 = 5
on remplace ( 1![]() x + 1
x + 1![]() 5) par (x + 5)
5) par (x + 5)
d ) Rendre compte :sous
forme d’une égalité :
3x + 15 = 3 ( x + 5 )
où le premier membre :
l’expression à factoriser : 3x + 15
le deuxième membre
est la factorisation terminée.: 3 ( x + 5 )
Conclusion
3x + 15 = 3 ( x + 5 )
Modèle mathématique(à
retenir)
Puisque ab + ac = a ( 1 ![]() b + 1
b + 1 ![]() c )
c )
On
retiendra que la forme : ab
+ ac = a ( b + c )
Remarque : Avant de procéder à la factorisation il
faut d’identifier un facteur commun:
Activité : RECHERCHE du FACTEUR
COMMUN
(Pour chaque cas , il faut appliquer la procédure
vue précédemment)
a) le facteur commun peut être un
nombre:
5 x + 15 =
donne « 5 ( x + 3 ) »
b) le facteur commun peut être une lettre
3x 2 +x =
donne « x ( 3 x + 1
) »
c ) les produits de facteurs sont
communs :
1°
) deux
termes de signe « + »
|
|
« ab + ab » = « 2 ab » |
|
ab + ab est égal à 2ab |
= ab ( 1 + 1 ) = ab (2 )
lire « a b fois 2 » qui s’écrira par convention (on place
le nombre en tête, dit aussi « le
coefficient » d’abord ) « ab + ab » a pour
forme factorisée « 2 ab » |
2 ° ) Et
deux termes de signe
« - »
|
|
« -ab - ab » = « -2 ab » |
|
-ab - ab = ?
que l ‘on peut écrire = 1 fois
(-ab) + 1 fois ( - ab) = 1 (-ab) + 1 ( - ab) -ab - ab est égal à -2ab commentaire : on a pris comme facteurs communs
le produit « ab » avec le
signe «- » ce qui ne sera pas possible dans le cas suivant… |
= 1 (-ab) +
1 ( - ab) = -ab ( 1 + 1 ) = - ab (2 )
lire « - a b fois 2 » qui s’écrira par convention (on place
le nombre en tête, dit aussi « le
coefficient » d’abord ) « -ab - ab » a pour
forme factorisée « -2
ab » |
3
° ) Deux termes de
signe « contraire »
|
|
« ab - ab » = « 0 » |
|
ab - ab que l ‘on peut écrire = ( +1
fois (ab)) + (- 1 fois ( ab)) = (+1 (ab)) + (- 1 ( ab)) ab - ab est égal 0 commentaire : on prend « ab » comme facteurs communs ,
remarquez que dans le cas précédent on a pris « - ab » comme facteurs communs parce que les deux termes
étaient négatifs. |
= ( +1 (ab) )+ ( - 1
( ab)) = -ab ( 1 +
1
) = - ab (2 )
lire « - a b fois 2 » qui s’écrira par convention (on place
le nombre en tête, dit aussi « le
coefficient » d’abord ) « ab - ab » a pour forme factorisée « 0 » |
d) Ce peut être un produit de facteurs:
9x2 -3x
= ; 3 x est le facteur commun ;
= 3 x ( 3 x -1)
e )le facteur commun peut être «le groupe de termes entre
parenthèse »
( x-1) 2 - (x- 1)
= (x-1
) [ (x-1) - 1 ] ; (x-1 ) est le facteur commun
(
2 x + 1 )2 + (2 x + 1) (x + 3) = ; (2
x + 1) est le facteur commun
( x+1) ( x +2) – 5( x +2)
= ; ( x +2) est le facteur
commun
f ) Grouper des termes semblables :
pour
cette somme algébrique, il est nécessaire de grouper les monômes semblables :
=3 ax2 - 1 + 6x + 5 –
3x – a x2
a) on groupe les termes en « x2 » :
3 ax2 – a x2 ; a x2 (
3 - 1 ) = a x2 ( 2
) = 2 ax2
b) on groupe termes en « x » :
6x – 3x = x (
6 –3) =
x (3) = 3x
3 ax2
- 1 + 6x + 5 – 3x – a x2
devient = 2 ax2 + 3x + 4
FACTORISATION d ’ un polynôme ( trinôme) du second degré: (forme : ax2 +bx +c )
(contenant
au plus trois termes dont un terme est
du second degré )
Exemple :x2
+ 2x -3
Nous
remarquerons qu’ il n’y a pas de facteur commun dans les trois termes ;;
La factorisation de cette forme n’est pas possible directement. On fera
appelle à d’ autres connaissances .
Ces connaissances sont abordées dans les deux
objectifs suivants :
|
Objectif : ( factorisation à partir des identités remarquables. Dit aussi
« égalités » remarquables) |
|
|
Objectif :
( factorisation des
polynômes du second degré) |
Remarque : on peut factoriser l’équation
dit « incomplète »
du second degré de la forme :
Dans ce cas on dit que le facteur commun est
« littéral ».
Soit le modèle a x² + b x qui devient x ( ax + b)
Exemples :
factoriser 4x² + 3x :
Le
facteur commun est « x » :
4x² + 3x devient x ( 4 x + 3)
factoriser 2x² + 8x
Le
facteur commun est « 2 x » :
2x² + 8x devient 2x ( x + 4)
( pour vérifier il suffit
de développer la forme factoriser)
INFORMATION :
Ces factorisations sont utilisées lorsque l’on veut « résoudre une
équation »
TRAVAUX AUTO _ FORMATIFS
|
1°) Quel
est le signe opératoire qui n’apparaît pas dans une expression
algébrique ? |
|
|
2°) Comment reconnaît - on un facteur ? |
|
|
3 °)Que peut-être « un facteur commun »
? |
|
|
4°)
Traduire en langage littéral: |
|
|
3 |
|
|
3x |
|
|
Ab |
|
|
x2y |
|
|
3(2x+1) |
|
|
2(x-3) |
|
|
x(x+1) |
|
|
(a+b)2
= (a+b) (a+b) |
|
|
(a-b)(a-b) = (a-b)2 |
|
|
(a+b)(a-b) = a2 - b2 |
|
|
5°) Donner la procédure qui permet d’opérer une factorisation : |
|
SIMPLIFICATION :
1°) Simplifier : (supprimer les parenthèses)
( x + 5
) = ………. + ( x +3)
= …….. ; + ( x - 2 ) = ……… ; + ( - x - 3) = …….. ;
- ( x + 5
) = ……… ; -( x +3)
= ……… ; - ( x - 2 ) = …….. ; - ( - x - 3) = ……….. ;
2°) Simplifications d’écritures :
|
Départ |
Simplification et on regroupe (réduit) |
|
|
A = ( x + 3 ) + ( x - 5) |
|
|
|
C = ( x + 3 ) - ( x - 5) |
|
|
|
D = ( x - 1) - ( 2x - 3) |
|
|
|
E = 2 ( 3 +x ) - ( 2x +1) |
|
|
|
F = - 5 ( 4x - 1) + 3 ( 2x -1) |
|
|
|
G = ( 3x +1)- (5x +2) + ( 2x -3) |
|
|
|
H = ( x² + x +1) - (2x²- x) |
|
|
|
K = ( 5x² - x) - ( 2x² +3x - 1) +2 |
|
|
3°) Niveau
+ : on demande de simplifier l’écriture proposée.
|
Exercices. |
Résultat : |
|
|
A = 3 ( x -5) - x ( x -2) |
|
|
|
B= x² - 3 - (x - 1) ( x +1) |
|
|
|
C = - ( x +2) x + 3 ( x - 5) |
|
|
|
D = |
|
|
FACTORISATION :
|
Série 1 |
Niveau 5e |
|
Factoriser les expressions suivantes: |
|
|
5 + 35 = |
|
|
5 +25 = |
|
|
2x + 6 = |
|
|
6x + 3 = |
|
|
3x +5x = |
|
|
11x -8x = |
|
Remarque : il faut se souvenir qu ‘ une
« puissance » est une écriture
« condensée » de la multiplication , dit aussi
" produit de facteurs communs ".
Série 2
|
|
|
x2 + x = |
|
|
x3 +x2 = |
|
|
3x2 + 6= |
|
|
2 x2 +22 = |
|
Série 3 ( niveau 3e)
|
|
|
( x+1) ( x +2) – 5( x +2) = |
|
|
( 2 x + 1 )2 + (2 x + 1) (x + 3) = |
|
|
3 x (x + 2 ) + x ( x + 2 ) = |
|
|
(x+1) (2x+3) + (x + 1 ) ( 5 x +7 ) = |
|
|
( x - 1 ) 2 + ( x- 1 ) ( x + 3 ) = |
|
Série 4
|
Exercices |
Résultat |
|
Exercices |
Résultat |
|
A = 7a+21 |
|
A = 27 x - 36 |
|
|
|
B = 14a - 35 |
|
B = 2x + 2 |
|
|
|
C = |
|
C = 24 x - 9 |
|