Pré requis:

Expression et somme algébrique (calcul numérique) niveau 1

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : Voir les expression algébriques

Objectif suivant : Suite les expressions algébriques ;

Tableau 302 Liste des cours d’algèbre….

DOSSIER : N°3 : ALGEBRE (Définitions, vocabulaire ;…. suite) 

Définition des expressions : Monôme ;binôme ; trinôme ; polynôme ; polynômes entier ou rationnel ; termes ; termes semblables. « valeur numérique d’un polynôme » ;

TEST

COURS

Devoir Contrôle

Devoir niveau I évaluation

Interdisciplinarité

Corrigé Contrôle

évaluation Corrigé

Evaluation niveau II	corrigé:
Evaluation niveau III	corrigé :

INFORMATIONS:

* Ne pas confondre le signe + du nombre relatif avec le signe opératoire de l’addition (+) ,pour savoir si le signe " + " est un signe opératoire ou le signe " + " appartenant à une valeur absolue ,nous devrions savoir si le nombre précédé du signe « plus » (appelé valeur numérique dit aussi valeur arithmétique ) est un nombre relatif (il appartient à l’ensemble des nombres relatifs).

Se souvenir :

1. Le résultat de l’addition s’appelle «  la somme »

2. Le résultat de la soustraction s ’appelle « la différence »

3. Le résultat de la multiplication s’appelle « le produit »

4. Le résultat de la division s’appelle « le quotient ».

5.

Rappels "informations"

COURS

Monôme :

On appelle "monôme " une expression algébrique qui ne renferme ni le signe + ni le signe - .

Exemples : 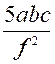;  ; 3 x² ; 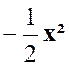sont des monômes.

Les multiplicateurs 5 et 2 , sont appelés « coefficients » ; on les écrit toujours avant les lettres .

Une lettre qui n'est pas précédée d'un coefficient est considéré comme ayant le coefficient 1 : Exemple : a² équivaut à 1 a²

Polynôme :

On appelle "polynôme " une expression composée de plusieurs "monômes" réunis par les signes + et - ; les monômes qui composent un polynôme sont appelés les "termes" du polynôme.

Termes semblables:

On appelle "termes semblables" d'un polynôme des termes qui ne diffèrent que par les coefficients.

Ainsi l' expression 8a² +3bc + 5d² - 4a²

Est un polynôme .( 8a² , -4 a² sont des termes semblables.)

Remarques :

Un polynôme est une expression algébrique ,que l'on devrait transformer en somme algébrique: ainsi le polynôme s' écrira :

( +8a² ) + (+3bc) + ( + 5d² ) + ( -4 a²)

Ainsi les termes du polynôme sont : ( +8a² ) , (+3bc) , ( + 5d² ) , ( -4 a²)

Dans un polynôme (ou expression algébrique): 8a² +3bc + 5d² – 4 a²

On considère ordinairement comme faisant partie d'un terme le signe qui le précède. Les termes du polynôme précédent sont : 8a² ; +3bc ; + 5d² ; -4 a²

8a² ; -4 a² sont des termes semblables.

Lorsque le premier terme d'un polynôme n'est pas précédé d'un signe , il est considéré comme précédé du signe +

Ainsi : a² + ab - b² équivaut à + a² + ab - b²

Inversement , si , à la suite d'une opération , on est amené à écrire comme premier terme d'un polynôme un terme précédé du signe + , on se dispense d'écrire ce signe devant le premier terme .

Les termes précédés du signe + sont dits "positifs"

Les termes précédés du signe - sont dits "négatifs"

Binôme :

On appelle "binôme" un polynôme qui n'a que deux termes .

Ainsi , le polynôme a² - b² est un binôme .

Trinôme :

On appelle "trinôme" un polynôme qui n'a que trois termes .

Ainsi , le polynôme ax² - bx + c est un trinôme .

Polynôme entier ou rationnel :

On dit qu'un polynôme est entier ou rationnel ou plus simplement entier ,quand les différents termes qui le composent sont rationnels et entiers.

Valeur numérique d'un terme :

On appelle " Valeur numérique d'un terme " le nombre obtenu en remplaçant les lettres par les valeurs numériques qui leur sont attribuées .

Ainsi , soit le terme 4 a²b³ :

sa valeur numérique pour a = 5 et b par b = 6 est le nombre que l'on obtient en remplaçant "a" par 5 et "b" par 6 et en effectuant les calculs indiqués , c'est à dire le nombre

4 5²6³ = 21 600

Valeur numérique d'un polynôme :

La valeur numérique d'un polynôme est l' excès de la somme des valeurs numériques des termes précédés du signe + , sur la somme des valeurs numériques de termes précédées du signe - ( somme algébrique ).

Pour le calcul , l'ordre des termes n'intervient pas sur le résultat.

Si la somme des valeurs positives est supérieure aux valeurs négatives le calcul ne pose pas de problème . Si la somme des valeurs positives est inférieur aux valeurs négatives le calcul de la valeur numérique peut poser problème,(voir l'objectif de formation sur l' addition de deux nombres de signe contraire)

Lorsque, dans un polynôme , figurent des termes semblables , on groupe ensemble ces termes en effectuant une factorisation .

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Lire les définitions.

EVALUATION: NIVEAU I

Faire le calcul des sommes algébriques suivantes: (montrer les étapes successives de transformation; l’utilisation de la calculatrice est autorisée comme moyen de vérification ,mais attention il faut bien connaître sa machine, elle peut vous donner un résultat qui n’est pas conforme)

Première série:	Transformation expression en somme algébrique:
a) 3,7+ 5,9 - 50,4 =
b) - 4,8 +13,9 -3,1- 5,3 + 6,4 =

Deuxième série :

c) 9 = 3,7+ ( 8,2 - 6,3 ) =

d) 9 + 3,7 - (7,9 -12,2) =

e) ( 8,2 - 6,3 ) - ( 7,9 - 12,2) =

f) +3,7+ ( 8,2 - 6,3 ) - ( 7,9 - 12,2) =

Evaluation VI : niveau C.C.

SUJET : 4	TC2	E	T	C
Calculer la valeur numérique de l’expression A suivante : A = 2 a – 3ab + 2 ( b + c)
1°) pour a = 2,5 ; b = 0 ; c = 4,9
2°) pour a = 8,2 ; b = 7,1  ; c = 75,3
3°) pour a = 3,1 ; b = 10,05 ; c = 47,39

SUJET :5	TC2	E	T	C
Soit l’expression L = 2x + y + 3 ( y –z ) Calculer L dans les cas suivants :
1°) L en cm et x = 0,51 dm ; y = 0,137 m ; z = 5 mm
2°) L en m et x = 15710 mm ; y = 2000 cm ; z = 1,24 dam
3°) L en km et x= 5028 m ; y = 102, 57 hm ; z = 3km 28 dam 7m