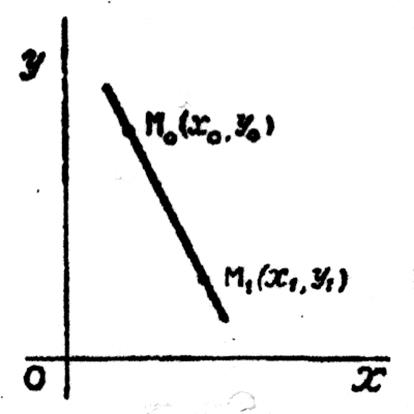Info pédagogique : cours niveau V
Ce cours est à maîtriser entièrement par les élèves Bac
prof. :
1°) il faut savoir
tracer une droite à partir d’un point
donné et connaissant la pente de
cette droite.
2°) savoir tracer la droite
tangente en un point d’une
courbe et connaissant sa dérivée en ce
point.
Pré requis:
|
|
|
|
|
ENVIRONNEMENT du dossier:
AVANT :
|
APRES : 1°) Les droites croissante ; décroissante,.. |
Complément
d’Info :
|
||
|
|
|
|
|
|
TITRE : LE COEFFICIENT DIRECTEUR « m »
d’une DROITE d’équation « y = m x +
p »
-
Activités : Tracés de droites
-
Le
coefficient directeur et « tangente »
-
Tracer
une droite connaissant un point et son coefficient directeur.
-
Calcul
du coefficient directeur d’une droite.
-
Relation :entre « coefficient directeur » et
« tangente »
-
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique |
Physique Chimie Electricité |
Statistique. |
|
COURS
|
|
Activités : Tracés de droites |
|
Dans tout ce qui suit le plan est muni d’un repère ( O, I, J) ou ( O , ![]() ,
, ![]() )
)
Première série de tracés :
|
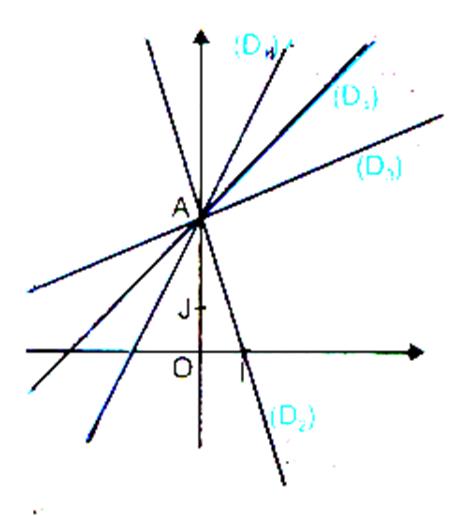
On a tracé les quatre
droites (D1) ; (D2) ;
(D3) ; (D4) suivantes données par leur équation de
la forme : y = m x + p |
|
|
D1) ; y = 2 x + 3 |
|
|
(D2) ; y = -3x +3 |
|
|
(D3) ; y = |
|
|
(D4 ; y = x +3 |
|
- Que constate-t-on ?
on constate que les droites ont
un point commun ;
- Quelles sont les coordonnées du
point « commun » ?
les
coordonnées du point A est ( 0 ;+3)
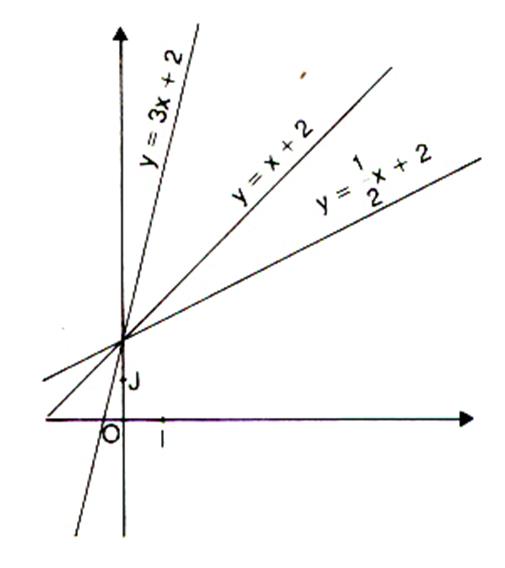
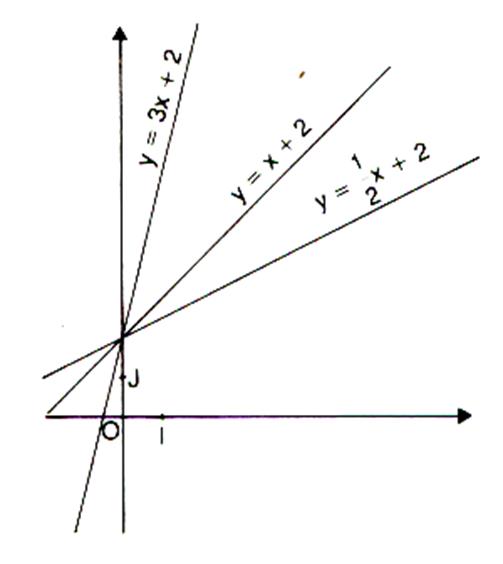
Deuxième série de tracés :
On a tracé les trois droites (D1) ; (D2) ;
(D3) ; suivantes données par leur équation de la forme : y
= mx + p
|
(D1) |
(D2) |
(D3) |
|
|
y =
3 x + 2 |
y =
x + 2 |
y = |
|
|
|
|||
Imaginons
que ces droites représentent le profil d’une route en montagne.
Classer dans l’ordre croissant de
celle qui monte le moins à celle qui monte le plus : (D3) ; (D2) ; (D1)
Que est la relation ( valeur ) dans l’équation
qui lie l’inclinaison ; la
« pente » et le tracé : ![]() ; 1 ; 3
; 1 ; 3
Comparer les valeurs numériques et ces inclinaisons de droites : plus le nombre est
grand plus la pente ( l’inclinaison) est grande .
On obtient deux classements identiques , le
coefficient « m » de l’équation
y = mx + p renseigne sur la direction
de la droite .
Définition du coefficient directeur :
Si une
droite a pour équation y = m x + p , le nombre « m » est appelé « coefficient
directeur de la droite »
Remarque :
le coefficient directeur peut être positif ou négatif.
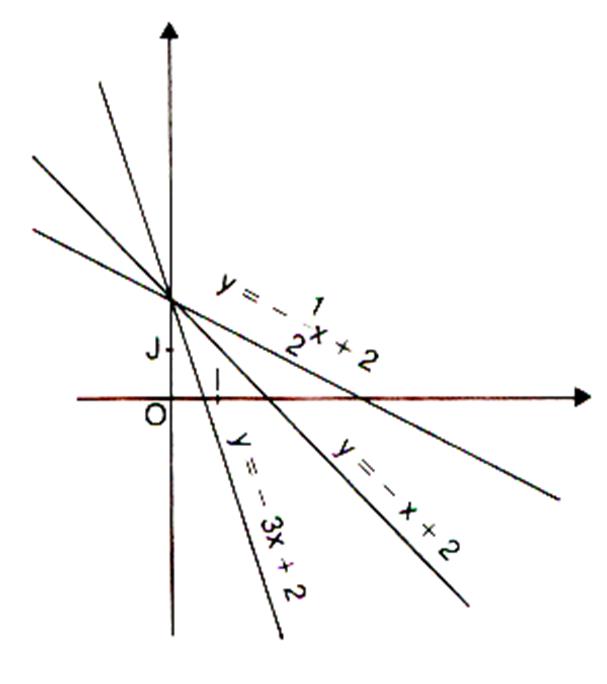
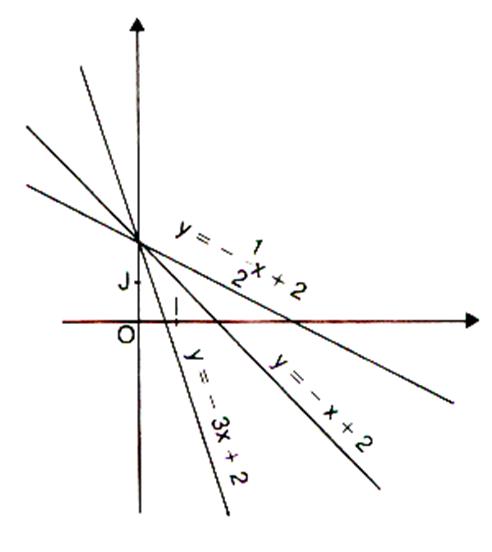
troisième série de tracés :On a
tracé les trois droites (D1) ;
(D2) ; (D3) ; suivantes données par leur équation
de la forme : y = m x + p
|
(D1) |
(D2) |
(D3) |
|
|
y = -3 x + 2 |
y = - x + 2 |
y = - |
|
|
|
|||
Imaginons
que ces droites représentent le profil d’une route en montagne.
Classer dans l’ordre de celle qui descend le moins à celle qui monte le plus .
Que est la relation ( valeur ) qui lie la « pente » et le tracé.
Remarque :
le coefficient directeur peut être positif ou négatif.
Que
l’on note : m >
0 et m <
0
|
Cas m <
0 |
Cas m >
0 |
|
|
|
En conclusion :
Le coefficient directeur indique comment varie l’ordonnée d’un point de
la droite ( D) si l’abscisse augmente d’une unité .
Soit ( D
) une droite de coefficient directeur « m » : si l’abscisse « x » augmente de « 1 » , alors
« y » augmente de la valeur de « m ».
II)Tracer
une droite dont on connaît un point (ses coordonnées) et le coefficient
directeur de cette droite.
« Construire
une droite sans chercher son
équation » :Dont on connaît le coefficient
directeur et les coordonnées d’un point appartenant à la droite ( D )
|
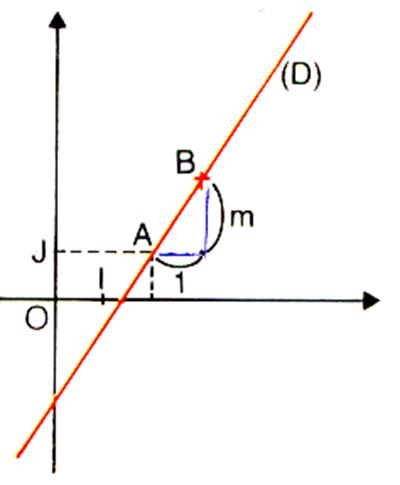
Procédure : Equation de
la forme « y = m x +p » |
Application : |
|
On connaît « m » et A ( xA; y A) |
Soit m = 3 ; et A ( -1 ; +2 )
|
|
On place le point A |
Placer A ; coordonnées x A = -1 ; y A=
+2 |
|
On place un point B dont les coordonnées sont (xA + 1) ; (y A +
m ) |
On place un point B dont les coordonnées sont : ( x A
+ 1) ; (y A + m ) soit
(-1 + 1) ; (2 + 3 ) ; soit les coordonnées de B ( 0 ; 5) |
|
On trace la droite ( D) qui passe par les deux points
|
|
Remarque :
( D) est une droite de coefficient directeur « m ».
Si l’abscisse augmente de « 1 » ,
l’ordonnée augmente de « m ».
Si l’abscisse augmente de « 3 » ,
l’ordonnée augmente de « 3m ».
Si l’abscisse augmente de « a » ,
l’ordonnée augmente de « am ».
|
II
) Relation :entre « coefficient
directeur » et « tangente » |
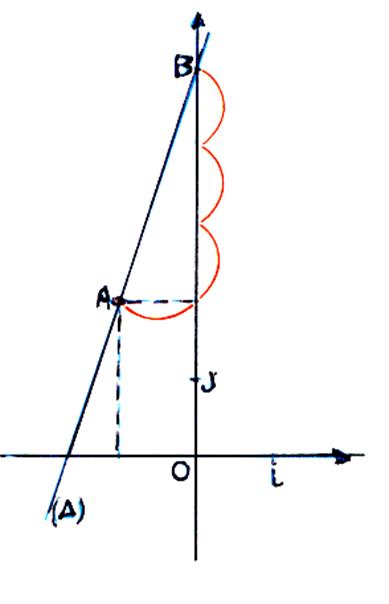
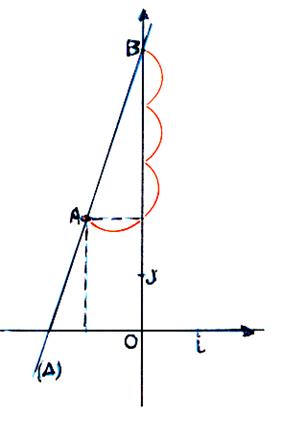
Activité :
Le repère ( O ; I ; J ) est
orthonormal .
1°) Construire une droite d’équation : y = 2x –1
2°) si x= 0 alors y = -1 :
la droite (D) coupe l’axe ( OJ) en « A » de coordonnées ( 0 ;-1).
3°) tracer la parallèle à ( O I ) menée par
« A »
4°) tracer la parallèle à (O J ) menée par I ( 1 ; 0 )
suite de
questions :
5°) Trouver les coordonnées du point « B »
( la droite ( I B ) coupe ( D ) en « C » )
6°) trouver les coordonnées du point « C »
7°) Pourquoi le triangle ABC est « rectangle » en B ?
8°) calculer AB ; puis BC ; puis tan ![]()
Réponses :
1°) Les droites sont parallèles aux axes ; le repère est orthonormal ,cela signifie que les axes
sont perpendiculaires et que OI = OJ =
1 unité.
2°) Tan a
= ![]() = m
= m
3°)on trouve : tan ![]() = 2 ; qui est égal au « m » de
l’équation y = 2x -1
= 2 ; qui est égal au « m » de
l’équation y = 2x -1
d’où la
propriété suivante :
Si ( D) est une
droite de coefficient directeur « m » positif et si l’angle a mesure l’angle aigu formé par ( D ) et l’axe des
abscisses alors : Tan a = m
|
III)
Calcul du coefficient directeur d’une droite : |
|
|
Problème :on veut calculer le
coefficient angulaire de la droite (non parallèle à l’axe Oy)
passant par deux points M0 et M1 .(on dit aussi :
« droite définie par deux points ») M0 à pour coordonnées ( x0 ; y0) et M1 a pour coordonnées ( x1 ;
y1) . L’équation de la droite passant par M0 et M1 est
de l a forme « y = mx +b » Cette droite passe par M0 : donc y0
= mx0 +b Cette droite passe par M1 : donc y1
= mx1 +b |
|
Calcul : on obtient un système : 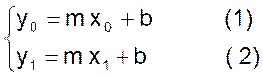
Attention !!!: On calculera (2) moins (1)
parce que l ‘abscisse le plus
éloigné du point « Origine » appartient à « M1 » :
Aussi y1
- y 0 = mx1 +b
- ( mx0
+b)
y1
- y 0 = mx1 +b
- mx0 - b
y1
- y 0 = mx1 - mx0
y1
- y 0 = m (
x1 - x0 )
puisque ( x1 - x0 )
≠ 0 on peut écrire que 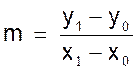
On obtient le théorème suivant : Le coefficient angulaire de la
droite passant par deux points est égal au quotient de la différence des
ordonnées des deux points par la différence correspondante de leurs abscisses.
Activité :
Exercice 1 : chercher le coefficient angulaire de la droite AB définie par les points A ( x= - 2 ; y = +3) et B ( x = + 2 ; y = +1)
►cette équation est de la forme y = mx +b ,
Les inconnues du problème sont « m » et « b »
On obtient deux équations en « m » et « b » en remplaçant
« x » et « y » par les coordonnées de « A » , puis par les coordonnées de « B ».
On remarque que « x B
> x A » on
écrira que m = 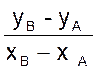
Recherche de « m » :
Première méthode :
Pour A : +3 = -2
m + b
( 1) ;
pour B : +1 =
+2 m + b (2)
On pose (2) - (1)
( +1) - ( + 3 ) =
( 2 m + b ) - (- 2m + b )
(+ 1) + (- 3) = 2 m + b + 2m - b
-
2 =
4 m
m = ( - 2 / 4 )
m = - 0,5
Deuxième méthode : on utilise le théorème
,on sait que : 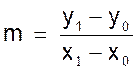 ; on adapte au point « A » et
« B » ; on obtient : m
=
; on adapte au point « A » et
« B » ; on obtient : m
= 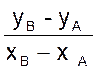
on remplace les lettres par les
valeurs et l’on calcule :
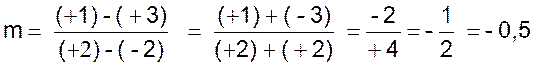
► par la suite on demandera de rechercher
l’équation de la droite passant par « AB ».
pour cela on remplacera la valeur de « m » dans une des
équations ( 1) ou ( 2) pour trouver par calcul la
valeur de « b » .
exemple :
(1) :
+3 = -2 m +
b ; +3
= -2 ( -0,5) + b ;
+ 3 = 1 + b ; b = 3 -
1 ; b = 2
(2) +1
= +2 m + b ; +1 = + 2 ( - 0,5) + b ; +1 = -1 + b ; b = 1 + 1 ; b = 2
on remarque que l’on trouve la
même valeur pour « b » ( ce qui est normal).
Conclusion : l’équation de la droite passant par « AB » est y = - 0,5 x
+ 2
|
Fin du cours : |
Pour en savoir +++Info : voir « résumé » |
TRAVAUX AUTO FORMATIFS.
- Donner la procédure permettant de
tracer une droite à partir d’un coefficient directeur et un point appartenant à
la droite .
Tracer
une droite : dont on connaît m =
3 ; et A ( -1 ;
+2 )
corrigé CONTROLE:
Donner la procédure
permettant de tracer une droite à partir d’un coefficient directeur et
un point appartenant à la droite .
|
Procédure : Equation de la forme « y = m x +p » |
|
On connaît « m » et A ( xA; y A) |
|
On place le point A |
|
On place un point B dont les coordonnées sont (xA + 1) ; (y A
+ m ) |
|
On trace la droite ( D) qui passe par les deux points |
corrigé EVALUATION:
Tracer une droite : dont on connaît
m = 3 ; et A ( -1 ; +2 )
|
Soit m = 3 ;
et A ( -1 ;
+2 ) |
|
Placer A ; coordonnées x A= -1 ; y A=+2 |
|
On place un point B dont les coordonnées sont : ( xA + 1) ; (y A + m )
soit (-1 + 1) ; (2 + 3 ) ; soit les coordonnées de
B ( 0 ; 5) |
|
|