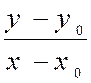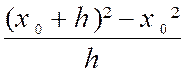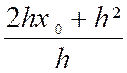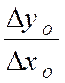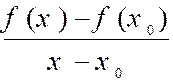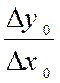la tangente en un point d'une courbe.

Pré requis :

Tangente .
Lecture : exemple N°8 ; Notions sur les « limites »

Environnement du dossier :

Index « warmaths »

Objectif précédent :

1. Coefficient directeur d’une droite

2. Tangente à un cercle.

Objectif suivant

1°) la fonction linéaire

2°) Application aux problèmes sur les tangentes à une courbe.

1°) La trigonométrie : sommaire

2°) Les dérivées (sommaire)

	DOSSIER : « TRIGONOMETRIE » et « recherche du nombre Dérivé »
	TANGENTE en un point d’une courbe. Pour conclure par la définition de « la dérivée »

	I ) Nombre dérivé et tangente ; pour établir la définition de « la dérivée ».
	II ) Dérivée d’une fonction( définition) .
	( Notation )

TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité Calcul : fonction linéaire. Calcul : fonction affine	Corrigé Contrôle	Corrigé évaluation

COURS

Ce cours conduit à la définition du nombre dérivé (dit aussi : dérivée)
Nombre dérivé et tangente ; pour établir la définition de « la dérivée »
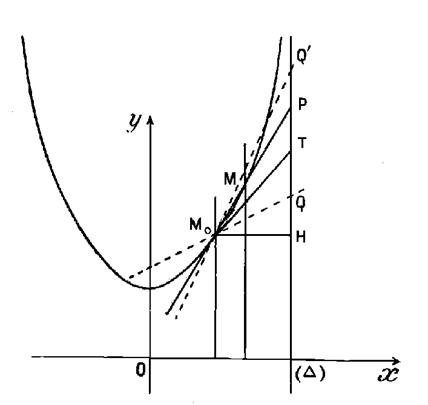
Considérons la courbe (ci contre) représentative de la fonction « » et soit le point « M₀ » appartenant à cette courbe dont l’abscisse est « x ₀ » La droite sécante « « M₀ M » qui joint le point « M₀ » à un autre point de la courbe d’abscisse « x » a pour pente : ( complétez le dessin ci-contre ….. )
Désignons par « » la différence « ₀ » on aura : « » ; qui s’écrit
Puisque « » alors

La pente est donc : = qui devient ( après développement et factorisation ) = = 2 x₀+ h
La pente est de « 2 x₀+ h »
Considérons la droite (delta) « » parallèle à « Oy » d’abscisse « x ₀ + 1 » ; la droite sécante la coupe en un point « P » et la parallèle à « Ox », menée par « M₀ », la coupe au point « H » ; le nombre mesure la pente de la sécante ; donc : « = 2 x₀+ h »
Portons le segment « HT » mesuré par « 2 x_O » : « = 2 x_O »
On aura : « = - = h »


Lorsque l’on donne à « » des valeurs voisines de « 0 » , le segment « TP » a une longueur voisine de zéro ( 0) , et lorsque « h » devient égale à zéro , le point « P » vient se confondre (on dit aussi : se superpose) avec le point « T » . La droite « M₀ M » ou « M₀ P » , qui pivote autour de « M₀ » , vient alors se confondre avec « MT » .

Or, dire que « » se rapproche de zéro ( 0) ou que « » tend vers zéro ( noté : ) , c'est-à-dire que le point « M » se rapproche du point « M₀ »,jusqu’à se confondre avec lui ; la sécante se confond alors avec la droite : « M₀ T» qu’on appelle « la tangente »,en « M₀ »,à la courbe. On dit aussi que , lorsque « h » a pour limite « zéro » , la pente « »a pour limite « 2 x₀+ » soit : « 2 » et la sécante a pour limite « M₀ T» .

Ainsi :
La tangente en un point d’une courbe est la position limite d’une sécante passant par ce point et un point voisin de la courbe, lorsque ce point vient se confondre avec le premier point.


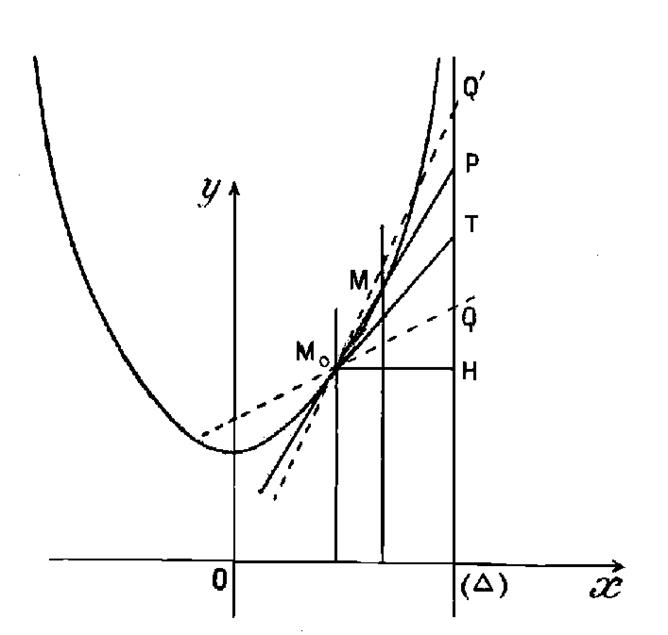
Remarque : (voir le dessin ci contre) Menons de part et d’autre de « M T» avec un même angle « » arbitrairement petit . Ces droites coupent « » aux points « Q » et « Q’ » ; on voit que , lorsque « h » est , en valeur absolue , inférieur à la plus petite des longueur « TQ » et « TQ’ » , la sécante « M₀ M» reste à l’intérieur de l’angle formé par les deux droites « M₀ Q» et « M₀ Q’», et contenant la bissectrice « M₀ T». Ainsi lorsque « h » est assez petit, la sécante fait avec la tangente un angle inférieur à tout angle arbitraire choisi « ».
Le nombre « h » s’appelle « accroissement de la variable « x » », on le désigne aussi par « « x_O» ; le nombre « y – y_O » est l’accroissement de la fonction : on le désigne par « k » ou « y _O»
La pente de la sécante est alors ou et la pente de la tangente est la limite du rapport lorsque « h » tend vers zéro , ou du rapport lorsque « x_O» tend vers zéro.
Ceci termine ce cours sur la tangente en un point d’une courbe……

	Pour arriver à la définition de la « dérivée »
	II ) Définition d’ une Dérivée d’une fonction.

Qui dit : Par définition :On appelle « dérivée d’une fonction » de la variable « » , pour une valeur « x_O» de cette variable, la pente de la tangente au point correspondant de la courbe représentative….

La dérivée est donc la limite de l’un des rapports :
		ou	ou	ou

Lorsque le dénominateur tend vers zéro. Cette limite est désignée par la notation : « » ou


Pour un monde plus juste : Ceux qui profitent peuvent partager et donner….. Aussi je vous demande d’ Aidez ce site à exister et à se développer en versant une participation financière à : warmaths – 1 b rue de l’abbaye _02120 Vadencourt.
Le papier nécessite du bois mais aussi de l’énergie et du pétrole afin d’être fabriqué , transporté, vendu , recyclé….. Contribuez au respect de l’environnement : imprimez les documents uniquement si vous en avez vraiment besoin.

TRAVAUX AUTO - FORMATIFS

CONTROLE

EVALUATION.