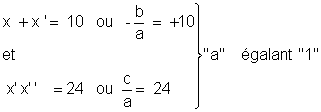|
Pour Aide et Formation Individualisée |
Série 3 |
|||
|
Matière :
MATHEMATIQUES |
« TRAVAUX » |
|||
|
|
|
|||
|
TITRE : le second degré et applications
en interdisciplinarité |
||||
|
|
||||
|
OBJECTIFS : - Savoir |
||||
|
I ) Pré requis: (pour remédiation ou
mise à niveau) |
|
|
|
|
ICI pour aller directement aux informations « cours » |
|
|
|
Info sur : La parabole .
: |
|
|
Leçon |
Titre |
||||||||
|
|
le second degré et applications en
interdisciplinarité ( suite 3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
Dans ce document vous
trouverez des applications du second degré.
Série 1 : EQUATIONS INCOMPLETES
de
la forme : y = ax²
Série 2 : EQUATIONS COMPLETES
de
la forme : y = ax² + bx + c
|
Série 1 : EQUATIONS INCOMPLETES
de la Forme y = ax² |
|
Physique N°1 : |
|
On
demande le temps que mettrait un caillou
tombant de la tour Eiffel sur le sol ,
sachant que la hauteur de la tour est
de 300 mètres et que la formule de la chute des corps est : Espace
parcouru noté (e) : ( « g » est l’accélération
gravitationnelle dont on prendra pour valeur 9,80 m .s-2
) et « t » est le temps) , on négligera la résistance de l’air. |
|
Solution : On
remplace dans l’équation (1) Ce
qui donne après transformation : Ici
la solution positive est la seule admissible . le caillou mettrait environ
7 secondes pour toucher le sol . On
apprend en Physique que les espaces parcourus par un corps qui tombe
librement sont « proportionnels
aux carrés des temps employés à les parcourir ».On
obtiendrait dans la représentation graphique
d’une demi - parabole .
|
Physique n°2 :
|
On
demande de calculer l’espace parcouru par un corps qui tombe : pendant
la première seconde ; puis après deux secondes ,
puis après trois secondes, etc. On
ne tiendra pas compte de la résistance de l’air.) |
|
|
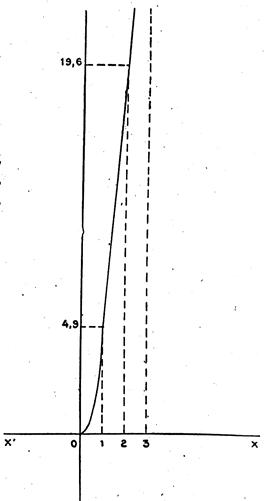
Solution : D’après la formule on a : Après la première
seconde : Après la deuxième seconde
: Après la troisième seconde :
Et ainsi de suite : Nous pouvons représenter
graphiquement cette fonction :
qui est de la forme y = a x² où « a » est représenté par
« 4,90 » |
|
|
En
remplaçant « x » et « y » par leurs valeurs ci dessus , et en portant celles - ci sur les axes on obtient des points d’intersections
. Si l’on joint ceux ci on trouve la
moitié d’une parabole ; car ici , on ne peut
pas envisager des valeurs négatives de « x » . (comme au Pb N°1
précédent). Commentaires :
1 : le coefficient de « x² » est ici « 4,9 »
représenté par « a » qui est donc un nombre positif. La parabole n’aura donc que la branche
positive. Commentaire
2 : cette branche appartient à une parabole qui est effilée ,
si l’on peut dire qu’une parabole dont le coefficient de « a »
serait égal à « 1 ». La
courbe précédente est la courbe de la chute des corps. On
peut y vérifier que les vitesses après chaque seconde sont proportionnelles
aux temps passés , ce qui se montre
expérimentalement en Physique. Effectivement :
L’ accélération : Dans
la première seconde , l’espace parcouru a été
de 4,90 m . Dans
la deuxième seconde , cet espace a été de 19,60 m - 4,90 m soit de
14,70 m ; c’est à dire de
4,90 m + 9,80 m
, après la première seconde la vitesse a donc augmenté de 9,80 m. Dans
la troisième seconde , l’espace parcouru a été de 44,10 m - 19,60 m soit de 24,50 m , c’est à
dire 4,90 m + 17,60 m
ou bien de 4,90 m + 2 fois 9, 80 m et ainsi de suite . La
vitesse augmente de 9,80 m à chaque
seconde. Ce nombre est appelé l’ accélération. |
|
|
Série 2 : EQUATIONS COMPLETES de la forme : y = ax² + bx + c |
||||||
|
Arithmétique . On achète un certain nombre de mètres de
tissu pour une somme de 600 euros. Si on avait payé le mètre 10 euros de moins ,
on aurait acquis 3 mètres de plus pour la même somme. On demande de calculer
le nombre primitif de mètres et le valeur primitif
du mètre. |
||||||
|
Soient
« y » le nombre primitif de
mètres et « x » le prix primitif du mètre. On
tire l’ équation ( 1 ) : x y = 600
(euros) D’autre
part , on peut aussi tirer de l’énoncé , la 2ème
équation ( 2 ) : ( x - 10 ) ( y + 3 ) = 600 (euros) Nous
tirons la valeur de « x » , dans
l’équation ( 1 ) et nous la portons dans l’ équation ( 2) , on a : ( 600 - 10 y ) ( y + 3 )
= 600 y 600 y - 10 y²
+ 1800 - 30 y = 600 y 10 y² + 30 y
= 1800 y² + 3 y
= 180 Nous
arrivons ainsi à l’équation complète du 2ème degré : y ² + 3 y
- 180 = 0 Première
façon de résoudre :
à partir de l’équation y² + 3 y
= 180 On
déclare que l’expression « y² + 3 y » est le commencement d’un carré parfait. On sait que le carré
d’une somme ( a + b)
est égal à : a² + 2 ab + b² Ici ,
« a² » est représenté par « y² » , de même
« 2ab » est représenté par « 3y », et par suite
« 2b » est représenté par « 3 » 2 b
= 3 On
peut avoir « b² » , ce sera : De
sorte que l’expression : y² + 3 y + Sera
le carré parfait de Ajoutons Ou :
Extrayons
la racine carrée des deux membres : |
||||||
|
|
|
|
||||
|
On
obtient deux réponses : |
||||||
|
|
|
|
||||
|
En
conclusion : la réponse positive est seule acceptable dans ce problème. Le
nombre primitif de mètres est donc bien 12 , et par
suite le prix primitif du mètre était
de : |
||||||
|
|
|
|
||||
|
Généralisation : |
||||||
|
Deuxième
façon de résoudre débouchant sur une généralisation. Nous
reprenons l’équation 10 y² + 30
y = 1800 Elle
peut se mettre sous la forme : 10 y ² + 30 y - 1800 = 0 Ou
encore sous la forme : 10
x ² + 30 x - 1800 = 0 Pour
plus de simplicité , on peut supposer que le nombre 1800
est positif , et l’on a :
10 x ² + 30 x + 1800 = 0 |
||||||
|
D’autre
part , nous remplaçons le coefficient
« 10 » par « a » , terme connu , le coefficient « 30 » par « b » ,
terme connu , et le nombre 1 800
, également terme connu , par « c ». On a l’équation type du 2ème
degré. a x² + b x + c = 0 |
||||||
|
Résolvons -
la , comme nous avons résolu
l’équation du problème : on a
successivement : a x²
+ b x = - c |
||||||
|
Divisons tout
par « a » : |
||||||
|
Complétons
le carré du premier membre en ajoutant aux deux membres la moitié du
coefficient de « x » , cette moitié étant
élevée au carré , et égalisons : |
||||||
|
Extrayons
la racine dans les deux membres : |
||||||
|
|
|
|
||||
|
Ou |
|
|
||||
|
Ou |
|
|
||||
|
Ou |
|
|
||||
|
Et
|
|
|
||||
|
Les
deux réponses sont : |
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
On
les appelle « les racines »
ou « les solutions » de l’équation. |
||||||
|
Règle : pour trouver la valeur de
« x » dans une équation
complète du 2ème degré mise sous la forme « a x² + b x + c = 0 » on
écrit que : « x »
est égal au coefficient de « b » changé de signe
, plus ou moins la racine carrée de la différence suivante ( carré du
coefficient de « x » moins 4 fois le produit du coefficient de
« x² » par « c »).
Le tout devra être divisé par deux fois le coefficient de « x² ». |
||||||
|
Remarque :
Trois cas peuvent de présenter dans le calcul des valeurs de « x’ »
et « x ‘’» |
||||||
|
1er
Cas : b² - 4 ac > 0 Dans
ce cas , l’ équation aura deux racines , c’est à
dire deux réponses , puisque la quantité sous le radical a une valeur
positive. |
||||||
|
2ème
cas : b² - 4 ac = 0 Dans
ce cas , la quantité sous le radical disparaît et on obtient : |
||||||
|
|
|
|
||||
|
|
|
|
||||
|
Il
n’ y a plus qu’une seule réponse , puisque les deux
racines sont égales. |
||||||
|
3ème
cas : b²
- 4 ac <
0 Dans
ce cas , la quantité sous le radical est négative ,
la racine ne pouvant pas être extraite
, il n’y aura pas de racines , c’est à dire « pas de réponses ». |
||||||
|
|
|
|
||||
|
Résoudre :
10 y² + 30 y =
1800 Soit
x ² + 3 y - 180 = 0 |
||||||
|
On
écrira : |
|
|
||||
|
|
|
|
||||
|
L’expression
|
|
|||||
|
|
|
|
||||
|
L’équation
x ² + 3 y - 180 = 0 a pour racines : x’
= 12 ; x ‘’ = 15 |
||||||
|
|
||||||
RELATIONS ENTRE LES COEFFICIENTS ET LES RACINES DE L’EQUATION
|
De
la forme « a x² + b x + c = 0 » |
||
|
Somme
des racines : Nous
savons que les racines de l’équation sont : |
||
|
|
|
|
|
|
|
|
|
Faisons
la somme de ces égalités , on peut écrire : x’
+ x ‘’ = |
||
|
Les
fractions à numérateurs irrationnels s’annulent , et
il reste : x’ + x ‘’
= |
||
|
On
en conclut que : la somme des
racines est égale au quotient changé de signe du coefficient (b) de « x » par le coefficient (a ) de « x² » |
||
|
Produit
des racines . |
||
|
|
||
|
Le
produit des numérateurs est :
|
||
|
Le
produit des dénominateur est : 2 a
´ 2 a = 4
a² |
||
|
En
dernière analyse on a : |
||
|
On
en conclut que : le produit des racines est égal au quotient du terme
connu, représenté par « c »
avec son signe , par le coefficient (a) de « x² » |
||
|
APPLICATION :
Conduisant à la
factorisation : Former
une équation du second degré , connaissant ses
racines ; Ces
racines sont :
+ 1 et |
||
|
On
a la « somme des
racines » : + 1 +
On
a le produit des racines
on
voit que , dans l’équation demandée ,
« a » est représenté par + 4 , « b » par «3 » et
« c » est représenté
par « -7 » . On
aura donc l’équation : 4 x² + 3x - 7 = 0
|
||
Problème de géométrie :
|
On
demande de calculer les deux côtés d’un rectangle ,
sachant que le périmètre est de 68 mètres et que la diagonale mesure 26
mètres. |
|
Solution : Soient
« x » et « y » les côtés du rectangle ; On a les
équations suivantes : 2 ( x + y ) =
68 ( 1 )
voir périmètre du rectangle « 2 ( L + l ) » x²
+ y² =
26 ² ( 2 )
voir « Pythagore » Nous
cherchons la valeur de « y »
dans l’équation (1) , et nous introduisons cette
valeur dans l’équation (2) . On a : x
+ y = y = 34 - x et x² + ( 34 - x ) ²
= 676 on
développe : x² + 1156 + x² - 68 x = 676 après
réduction on obtient : x²
- 34 x + 240 = 0 On
tire les valeurs de
« x » : Les
deux réponses sont : x ‘ = 24
; x’’ = 10 Ces
deux réponses sont acceptables , en ce sens donnent
les valeurs des deux côtés du rectangle. |
|
|
ARTIFICES DE CALCULS :
|
La somme de deux nombres étant
« 10 » et leur produit
« 24 », quels sont ces deux nombres ? Résolution n°1 On aura évidemment les deux équations : (1)
x + y = 10 (2)
x y = 24 En introduisant dans l’équation (1) la valeur de
« x » tirée dans l’équation (2) , on aura : et y² - 10 y + 24
= 0 ce qui donne : Commentaire
1 : résolution n°2 On voit
qu’il a fallu appliquer ici les règles de résolution de l’équation du second degré . On aurait pu éviter cette résolution par
l’artifice de calcul suivant : Nous élevons au carré l’équation (1) et
quadruplons l’équation (2) ; On aura : x² + y ² + 2 x y
= 100 4 x y
= 96 Soustrayons membre à membre ces deux équations , on a :
x² + y² - 2 x y =
4 [ soit ( x - y ) ² = 4
] Effectuons la racine carré de chaque
membre : x - y = 2 (3) Additionnons les équation ( 1)
et ( 3) x + y
+ x - y = 10 + 2
2x = 12 x = 6 alors de ( 1) x + y =
10 on obtient : 6 + y
= 10 donc « y = 4 » Commentaire 2 : résolution n°3 aussi possible : On aurait pu , en
s’appuyant , sur les relation entre les coefficients et les racines , trouver
tout de suite l’équation :
l’équation
sera : x² - 10 x +
24 = 0 ; cette équation est
absolument identique à la précédente : « y² - 10 y
+ 24 = 0 » |
|
Problème de
Géométrie : On
demande d’inscrire, dans un demi -
cercle de diamètre AOB
, un rectangle dont on connaît
la surface. Le rayon « R » est connu et la surface sera
représentée par « m ». |
|
|
Soit le demi - cercle ci - contre : |
|
|
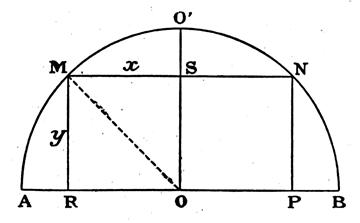
Solution : Supposons le problème résolu et le rectangle MNPR
inscrit dans le demi - cercle . Menons OO’ . On prendra comme inconnue : MS = x ;
et MR = y On pourra écrire l’équation :
« 2x » fois
« y » = m
soit 2 x y = m (1) D’autre part , en menant
MO , on a : y² + x²
= R² (2) On a à résoudre le système suivant : On additionne membre à membre :
y² + x² + 2 x y = R² + m soit
( y
+ x )² = R² + m On soustrait membre à membre :
y² + x² - 2 xy = R
² - m
soit ( y - x
)² = R² - m on tirera
x + y = et
x - y = On additionne : 2 x = On trouvera « y » en soustrayant les
équations (3) et (4)
Il y a donc les 2 réponses . Discussion : On voit que pour que le
problème soit possible
, il faut que R² - m
> 0 ou que R²
> m C’est à dire que le carré du rayon donné doit
être plus grand que l’aire de la surface donnée. 1°)
si R² > m , il y a donc deux solutions :
les précédentes . 2°) si R²
= m , les valeurs de « x » et
« y » sont les mêmes , c’est à dire :
Dans ce cas ,
« m » a pris la plus forte valeur qu’il pouvait prendre. Cette
valeur représente la plus grande surface que peut prendre le rectangle inscrit , et cette surface correspond à : x
= y c’est à dire que le rectangle aura pour
côtés : 2x et x et que dans la figure ,
on aura : M N = 2 MR Remarque : On dit alors que le rectangle
inscrit a pris le maximum de sa valeur , ses côtés variant , l’un ( MN) de 2R
à O et l’autre (MR) de O à R . 3°) Si R² < m ; le problème est impossible . |
|