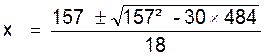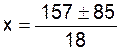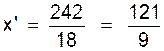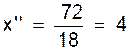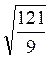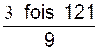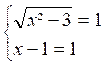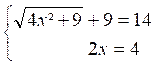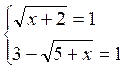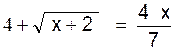Pré requis:
|
|
|
|
|
|
|
|
|
Environnement du
dossier :
DOSSIER Résolution d'une Equation IRRATIONNELLE :
|
► |
Cours n°1 Identification, Procédure à appliquer pour résoudre une équation
irrationnelle ;….. |
|
|
► |
Cours n°1 ( suite) : CAS : Définition ;
…..RESOUDRE UNE EQUATION POSSEDANT UN SEUL RADICAL. |
|
|
|
|
|
|
COURS |
Interdisciplinarité |
|
|
COURS 1 |
|||||
|
|
1°)
Définition : Une équation est dite
« irrationnelle » quand l’inconnue se trouve sous le radical. . Exemple :
3 x + 5 Supposons une équation A = B (1) Elevons au carré
les deux membres de cette équation , on a
: A² = B²
(2) Ces deux équations ne sont pas équivalentes .En effet , prenons la racine carrée des deux termes de
l’équation (2) , on aura :
± A = ±
B On a donc les solutions suivantes : + A = +
B (3) ; qui répond à l’équation (1) Puis on a aussi : + A = - B
(4) qui ne correspond plus à
l’équation (1) On aurait encore : - A = - B qui correspond à la solution (3) Et enfin
- A = + B qui
correspond à la solution (4) Pour s’assurer qu ‘ une des solutions trouvées
est la bonne , on remplace l’inconnue par les
valeurs trouvées, et on voit celle qui satisfait à l’équation proposée . Exemple : soit à résoudre : 3 x + 5 On s’arrange de manière à isoler l’expression
« 5 On a :
|
|
|||
|
|
|
5 |
( 2) |
|
|
|
|
|
25 x = 484 + 9 x² - 132 x |
|
|
|
|
|
|
9 x² - 157 x + 484 + 0 |
|
|
|
|
|
En appliquant la formule des résolutions des
équations du second degré , on obtient : |
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
||
|
|
Nous devons vérifier si ces valeurs
satisfont à l’équation (2) |
|
|||
|
|
Pour la
valeur « 4 » , on a : 5 10 = 10 |
|
|||
|
|
Pour la valeur « 5 ou Conclusion : Cette deuxième valeur n’est donc pas admissible. La seule valeur de « x » est
« 4 » . |
|
|||
|
|
Procédure à appliquer pour résoudre une équation
irrationnelle : Pour résoudre une équation irrationnelle : -
on isole d’abord le radical dans un membre . -
on élève ensuite les deux
membres de l’équation au carré. -
On résout ensuite . -
On vérifie si les
valeurs trouvées peuvent être admises. |
|
|||
|
|
|
|
|||
|
COURS 1 (suite) |
|
|
Définition : une équation irrationnelle est une équation
qui renferme un ou plusieurs radicaux
portant sur des expressions contenant l’inconnue. Dans le cas contraire, l’équation est dite
« rationnelle ». Nous allons voir que la résolution de certaines
équations irrationnelles se ramène à celle d’équations du premier degré. Exemple 1 : résoudre l’équation (1) S’il existe une valeur de « x » pour
laquelle les deux membres de cette équation sont égaux, pour cette valeur les carrés
des deux membres sont aussi égaux. Donc toute racine de l’équation (1) est racine de
l’équation : x² - 3 = ( x - 1)² Cette équation s’écrit : x
² - 3 = x² - 2x +1
2 x = 4
x
= 2 x = 2 est
donc la seule solution possible de l’équation (1) Pour voir si cette valeur est effectivement racine
de l’équation (1), il suffit de vérifier. Pour x = 2 , on a :
x = 2 est donc bien racine de l’équation (1) Exemple 2 : Résoudre l’équation (1)
S’il existe une valeur de « x » pour
laquelle les deux membres de cette équation sont égaux, cette valeur
satisfait aux équations suivantes : 4
x² +9 = (2x -9 )² 4
x² +9 = 4x² - 36 x + 81
36 x = 72
x
= 2 x = 2 est donc la seule solution possible de
l’équation(1) . Vérifions : Pour x = 2 , on a :
x = 2
n’est donc par racine de l’équation (1) et celle-ci n’admet aucune
solution. Exemple 3 : Résoudre
l’équation : (1) S’il existe une valeur de « x » pour
laquelle les deux membres de cette équation sont égaux, cette valeur
satisfait aux équations : x + 2 =
9 - 6 6 5 + x = 4
x = -1 Donc l’équation (1) a une seule racine
« possible » : x = -1 Pour voir si cette valeur est effectivement racine
de l’équation (1), vérifions. Pour « x » = -1 ,
on a
donc x = -1 est bien
racine de l’équation (1) CONCLUSION : Les exemples précédents nous montrent que les racines d’une équation sont racines
de l’équation obtenue en élevant ses deux membres au carré. D’une façon générale, soit l’équation (1)
A = B Et l’équation (2)
A² = B ² obtenue en élevant ses deux membres au
carré. Toute solution de l’équation (1) donne à A et à B
la même valeur ; elle donne donc la même valeur à A² et à B² , c’est à dire
que toute racine de l’équation (1) et racine de l’équation (2) . Mais réciproquement, nous ne savons pas si toute racine de
l’équation (2) est racine de l’équation (1). L’équation (2) est appelée
« résolvante » de l’équation (1). Si on sait la résoudre, ses
racines seront les seules solutions possibles de l’équation (1) .Il faudra
alors choisir celles de ces racines qui conviennent effectivement. Pour cela,
il suffira de vérifier. REMARQUE I : Dans l’exemple II , avant d’élever
au carré nous avons isoler le radical , c’est à dire mis ce radical
seul dans un membre. Si on avait en effet élevé au carré les deux
membres de l’équation donnée il serait resté un radical et le but cherché
n’aurait pas été atteint. REMARQUE II : Lorsqu’une équation irrationnelle
renferme plusieurs radicaux, pour obtenir une résolvante rationnelle, il est
en général nécessaire de faire plusieurs élévations au carré.(voir l’exemple III) REMARQUE III : L’équation obtenue en élevant les deux
membres d’une équation au carré est plus générale que « l’équation
primitive », c’est à dire qu’elle admet toutes les racines de cette
équation mais « elle peut en admettre d’autres ». Celles de ces racines qui ne conviennent pas à
l’équation primitive sont dites « étrangères » ou
« introduites par l’élévation au carré. CAS : RESOUDRE UNE
EQUATION POSSEDANT UN SEUL RADICAL. Si une équation irrationnelle ne renferme qu’un
seul radical, après avoir isolé celui-ci , l’équation
est mise sous la forme : (1) P et Q étant deux polynômes. Nous avons vu que toutes racine de l’équation (1)
est racine de l’équation (2) P = Q² obtenue en élevant les deux membres au carré. Mais
nous n’avons pas examiné si , réciproquement, toute
racine de l’équation (2) et racine de l’équation (1). C’est
pourquoi pour résoudre (1) nous avons dû « choisir » celles des racines
(2) qui conviennent à (1) en vérifiant. Nous allons voir s’il n’est pas possible de
trouver un « critérium » qui nous dispense de faire cette
vérification. Soit « x » = a (lire : alpha) une racine de
l’équation (2). Pour x = a , P et Q prennent des valeurs numériques P’ et
Q’ telles que P’ = Q’² Le nombre
P’, égal à un carré, est donc positif. Il a donc deux racines carrées,
l’une positive L’égalité précédente, nous prouve que Q’ est égal
à l’une de ces racines carrés, donc : Si Q’ "e 0
on a Et
si Q’ "d 0 on a
- Il revient au même de dire que : Si
Q’ "e 0
a est racine de l’équation Et
si Q’ "d 0 a est racine de l’équation - On voit donc que pour que « a » soit racine de l’équation (1) il faut et il
suffit que pour x = a , Q prenne une valeur positive
ou nulle. Remarquons qu’il est inutile de vérifier que
pour x = a la quantité sous le
radical P Prend une valeur positive ou nulle car cette
condition est toujours réalisée d’après ce qu’il a été dit précédemment ( P ‘ = Q’² ) Exemple : Résoudre
l’équation (1) Elevons les deux membres de l’équation au
carré ; on obtient la résolution : (2) 1
- 8 x = (x +1) ²
1 - 8 x = x²
+ 2x +1
x² + 10 x =
0 x ( x +10) = 0 Donc :
x = 0 et x = -10 Pour qu’une
racine convienne à l’équation proposée il faut et il suffit que pour cette
valeur on ait : x +
1 "e
0 c’est à dire x "e
- 1 Donc seule la racine x= 0 convient. Le raisonnement fait précédemment prouve que la
« racine étrangère » - 10 Convient à
l’équation - Obtenue en changeant le signe qui est devant le
radical. |
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|
|
- Donner la procédure à appliquer pour résoudre
une équation irrationnelle du premier degré . |
|
|
|
N° 1 résoudre : 3 x + 5 N° 2 : résoudre l’équation N°3
Résoudre l’équation N° 4
Résoudre l’équation : N°
5 Résoudre l’équation : (les corrigés sont dans le
cours) |
|
|
|
Série
2 : résoudre les équations irrationnelles
suivantes : |
|
|
1°) |
|
|
|
2°) |
|
|
|
3°) |
|
|
|
4°) |
|
|