Pré requis:
Arithmétique
|
|
|
|
|
Le
premier degré . ( exercices types et problèmes résolus)
|
|
|
|
|
Le
premier degré (suite) les mises en équations ( avec systèmes)
|
|
|
|
|
Calcul
numérique
|
|
|
|
|
Formation niveau V : le premier degré
|
ENVIRONNEMENT du
dossier:
|
Objectif suivant |
DOSSIER
: LES PROBLEMES DU PREMIER
DEGRE
Choisir
un domaine d’application ! ! !
|
|
|
|
Sport (
piste d'athlétisme) + ( un
problème d’arithmétique :dossier 145) |
||
Arithmétique et vie usuelle
|
||
|
Economie |
||
|
Les a% |
||
|
Géométrie |
||
|
Physique |
||
|
Chimie |
||
|
Série 2
Différentes applications . |
|
|
Problème de niveau I « des
tours de piste »: Calculs
numériques
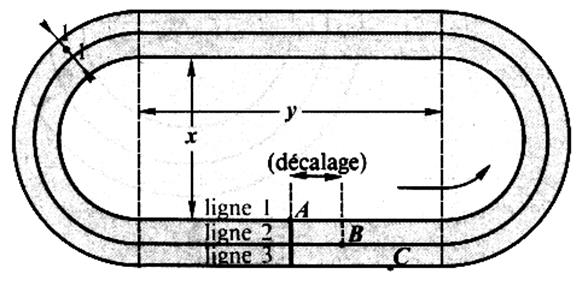
Une piste d'athlétisme possède 4 couloirs
, un couloir par coureur.
Dans le dessin ci- dessus les couloirs ne sont pas dessinés ,les lignes
représentent le milieu ( l'axe) de
chaque couloir.
"x" =
1°) Calculer la longueur du tour
de piste 1.
2°) Calculer la longueur du tour de piste 2.
3°) Calculer la longueur du tour de piste 3.
|
|
|
|
4°) Si l'on veut
que le coureur "B"
ligne 2 , parcourt la même distance que le coureur "A"
ligne 1 , il faut un "décalage" entre les coureurs "A" et
"B" (voir figure)
Calculer ce décalage .
5°) Montrer que le décalage entre les coureurs A et B et le même qu'entre les coureurs
"B" et "C" .
|
Sport : |
Algèbre . |
Problème de niveau II :
« Les tours de piste »
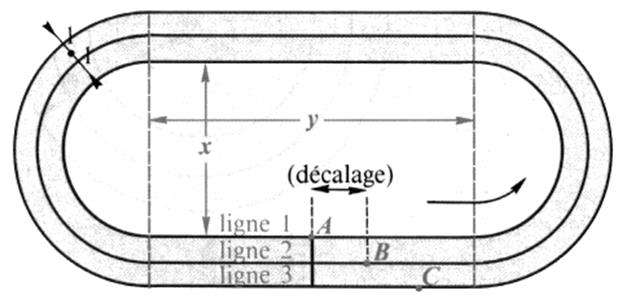
Une piste d'athlétisme possède 4
couloirs , un couloir par coureur.
Dans le dessin ci- dessus les couloirs ne sont pas dessinés ,les lignes
représentent le milieu ( l'axe) de
chaque couloir.
1°) Exprimer en fonction de "x" et "y" la longueur du tour de piste 1.
2°) Exprimer en fonction de "x" et "y" la longueur du tour de piste 2.
3°) Exprimer en fonction de "x" et "y" la longueur du tour de piste 3.
|
|
|
|
4°) Si l'on veut
que le coureur "B"
ligne 2 , parcourt la même distance que le coureur "A"
ligne 1 , il faut un "décalage" entre les coureurs "A" et
"B" (voir figure)
Calculer ce décalage . Dépend- il de "x" ? ; de
"y" ?
5°) Montrer que le décalage entre les coureurs A et B et le même qu'entre les coureurs
"B" et "C" .
Série 1 :
|
|
|
|
1°) Calculer deux nombres sachant que leur somme est 37 et
que leur différence est 13 .Généraliser. Résolution : 1°) choix de la ou des inconnues : « x »
le premier nombre et « y »
le deuxième nombre. 2°)mise en équation : a) x + y = 37 b) x – y = 13 première proposition de résolution : de « l’équation « b » x = 13 +y on remplace
dans « l’équation a » x + y = 37
d’où (13 + y) + y = 37 2y = 37 - 13 ; donc « y » = 12 on en déduit : x + 12 = 37 ; donc x =37
–12 ; x = 25 deuxième proposition de résolution : on additionne les deux égalités pour faire disparaître
« y » donc x + y + x – y =
37 + 13 2x = 50 x = 25 on remplace « x » dans une des équations : 25
+ y = 37 donc y = 37 – 25 ;
y = 12 le premier nombre vaut
« 25 » et le second nombre = 12 vérification : 25 + 12 = 37 et 25 – 12 = 13 |
|
|
2 °) La somme de deux nombres est 100 et en retranchant 1/6 du
plus grand pour l’ajouter au plus
petit , ils sont égaux. Quels sont ces deux nombres ? Résolution : 1°) choix de la ou des inconnues 2°)mise en équation 3°)résolution des équations 4°)discussion du problème |
|
|
3°)Quel est le nombre dont les 13 /20 surpassent de ¼ de 7 entiers
½ ? |
|
|
4°)Trouver deux nombres dont la
somme soit 19 et le produit 60 .(on
calculera l a différence de ces nombres en utilisant l’identité
remarquable : ( x + y )² – ( x - y )² = 4xy |
|
|
5°)Trouver deux nombres dont la différence soit 4 1/9 et le quotient
3/7 . |
|
|
6°)Un marchande d’œufs se
rendant au marché vend à un passant les 3/8 de ses œufs , à l’entrée de la
ville , elle vent encore les 2/5 des œufs qui lui restent , et elle
arrive au marché avec 360 œufs
.Combien en avait-elle en partant ? |
|
|
7°)Partagez une somme de 252 euros
entre trois personnes de telle
sorte que la seconde ait les ¾ de la
première et que la part de la troisième soit égale à la demi –somme des parts des deux autres . |
|
|
8°)Une pompe destinée à élever l’eau pour le service d’une usine met 10h 5/11 pour remplir le réservoir si elle
fonctionne bien .Par suite d’un accident , le rendement est diminué de 1/3
lorsque la bassin est plein au ¼. Combien mettra-elle ce jour là pour le remplir ? |
|
|
9°) Compagnies d’ouvriers sont
telles que la première aidée de la moitié de chacune des deux autres ,
exécuterait un certain travail en 27 jours ; la deuxième , plus la
moitié des deux autres , en 23
jours ; la troisième plus la moitié des eux autres en 19 jours. Combien ces trois compagnies
d’ouvriers travaillant ensemble mettraient-elles de jours pour faire
le travail ? |
|
|
10°) Un bassin est alimenté par 3 robinets , si l’on ouvre les deux
premiers , il se remplit en 3 heures , si l’on ouvre le premier et le
troisième ; il se remplit en 1heure 40minute , sachant que la capacité
du bassin est de |
|
|
11°) Il a été fabriqué en France , pendant l’année 1900 2 185 858
pièces d’or de 10 euros et de 20 euros
, pour une valeur totale de 28
012 830 euros
.Combien a-t-on fabriqué de pièces de 10 euros et de pièces de 20 euros. |
|
|
12°) Une montre avance de 10 mn en 24 heures , on l’ a mise à l’heure
à midi ; quelle heure est-il lorsqu’elle marque 6 heures. |
|
|
13°) Trois frères désirent acheter une maison valant 700 000 euros.
Aucun d’eux n’a assez d’argent ; si l’ aîné donnait au second 1/3 de ce qu’il possède ,
ou au troisième ¼ de ce qu’il possède ,chacun des deux aurait une somme suffisante
pour acheter la maison . Mais l’aîné emprunte au troisième la moitié de sa
fortune et achète la maison. Combien possédait chaque frère ? |
|
|
|
|
|
|
|
|
Une somme est déposée chez un banquier où elle porte
intérêt à 3 % l’an. On la retire au bout de 255 jours et l’on touche 2 859,50
euros pour le capital et les intérêts. Quelle somme avait-on placée ? |
|
|
Trouver le montant du capital tel que si on en place le 1/6 à 3% , la moitié à 5 % et
le reste à 6 % on obtienne au bout de 4 mois 1000 euros d’intérêt . |
|
|
|
|
|
|
|
|
1°) trouver les dimensions d’un rectangle sachant que si
l’on augmente la longueur de |
|
|
2°) Une roue de vélo a |
|
|
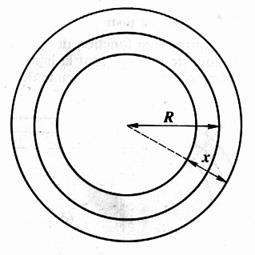
3°)On note "R" le rayon moyen de la couronne circulaire
ci contre . a) exprimer en fonction de "R" et "x" les
rayons extérieurs et intérieur de la couronne . b) En déduire que l'aire de la couronne est égale à 2 p R x |
|
|
|
|
|
|
|
|
|
|
|
On sait qu’en graduant un thermomètre centigrade on marque
0° dans la glace fondante et 100° dans la vapeur d’eau bouillante ; avec
le thermomètre Fahrenheit , on marque 32° et 212° à ces mêmes points fixes
.Deux thermomètres, un centigrade et un Fahrenheit peuvent-ils indiquer le
même degré de température dans un même bain ? Quelle est cette
température ? |
|
|
|
|
|
Un bateau fait en 10 heures 110 milles en suivant le courant et 70
milles en le remontant .Lors d’un autre voyage , il fait dans le même temps
88 milles en suivant le courant et 84 milles en le remontant . Combien de
milles ce bateau peut-il faire à l’heure dans une eau calme (vitesse propre
du bateau) et quelle est la vitesse du courant ? |
|
|
D’un train qui
marche à une vitesse de |
|
|
Une personne disposant de 4 heures pour faire une
promenade , part dans une voiture qui fait du |
|
|
Un coureur à pied par avec une vitesse de |
|
|
Deux véhicules vont dans la même direction il vont
parcourir le même trajet soit une distance de 15 km ; le premier
véhicule plus lent part avant .Au bout de 4 minutes le suivant décide de
rattraper son copain ; le premier véhicule roule
à une vitesse moyenne de Questions: Quel temps on mis les deux véhicules pour parcourir les 15
km ? au bout de combien de temps le second aura rattrapé le
premier véhicule ? quel temps s’est-il écoulé ? à quelle distance du but se rencontrerons
–t-ils ? |
|
|
|
|
|
|
|
|
On veut prépare Masse atomique du Cl 35,5 Masse atomique de l’O
16 Masse atomique du K
39 Masse du litre d’oxygène |
|
|
Quel volume d’hydrogène préparerait-on en attaquant |
|
|
|
|
N°1:
: Un rectangle a les
caractéristiques suivantes :
Son
périmètre mesure
Calculer sa longueur et sa
largeur .
N°2 :
Trouver 3 nombres entiers pairs consécutifs dont la somme est égale à 36 .
Donner la valeur du premier nombre.
N°3 :
Une ouvrier met 15 minutes pour usiner
une pièce , pour aménager et préparer le poste de travail il faut
prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?
Prendre
"x" le nombre de pièces.
N°4 : trouver trois nombres entiers consécutifs dont la somme est 1884
.( prendre pour inconnue , le plus petit nombre.
N°5 : Trouver 3 nombres
multiples de 3 consécutifs dont
la somme est 27
Prendre pour inconnue le plus petit nombre .
6 + 9
+ 12
N°6 : Trouver 5 nombres entiers impairs consécutifs dont la somme
est 75.
Info : prendre pour inconnue le
nombre médian ( celui qui se trouve au milieu )
Résultat : 11 ; 13 ;
15 ; 17
; 19
N°7 :Trouver 13 nombres
consécutifs dont la somme est 2457 .
Info : prendre pour inconnue le
nombre médian ( celui qui se trouve au milieu )
N°8 Quel nombre faut-il
multiplier 34 pour obtenir 25 ?
Interdisciplinarité
:
N°1 Le réservoir d'une voiture
est au deux cinquièmes rempli . Il faut ajouter
N°2 Le réservoir d'un voiture est vide aux deux tiers . On
ajoute 30 litres de carburant pour le remplir aux trois quarts . Quelle est la contenance
du réservoir ?
N°3 la largeur d'un rectangle est
le tiers de sa longueur et le périmètre mesure
N°4 La longueur d'un rectangle surpasse de
N°5 Le 1er janvier 1997 la population de la France
a été estimée à 58 494 000 habitants
se répartissent en 30 017 000
femmes et 28 477 000 hommes.
Quel pourcentage de la population les femmes et les hommes représentent
- ils ?
N°6 Augmenter un nombre de x % ,
c'est multiplier ce nombre par ( 1 + ![]() )
ou ( 1 + 0,01x )
)
ou ( 1 + 0,01x )
Pour calculer le pourcentage d'augmentation du prix d'un objet qui passe
de 34 à 39,5 € , on écrit : 39,5 = 34 (
1 + 0,01 x)
Ecrire cette équation sous la forme ax + b =
c , puis la résoudre ( arrondir à 0,01
près , ou à 2 décimales).
Enoncer le résultat sous forme
d'une phrase .
N°7 Calculer le pourcentage d'augmentation de la population d'un village
qui passe de 3764 habitants à 3978 .
N°8 un centre de formation
organise un voyage .Le transporteur propose un prix global correspondant à 160 €
par personne . Si le nombre de personnes augmente de 5 , on passe pour
le même prix global , à 120 € par
personne.
Combien de personnes participent au voyage ?
N° 9 La durée de fabrication
d'une pièce est de 6,50 mn.
Au cours d'une journée de 8 h , combien peut-on fabriquer de pièces sachant
qu'il faut compter 1 h 30 mn pour le réglage la machine et l'affûtage de
l'outil et l'approvisionnement .
N° 10
|
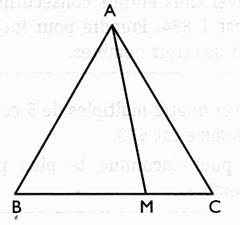
ABC est un triangle équilatéral de côté 1°) calculer la hauteur du triangle ABC , puis l'aire du triangle . 2) où doit -on placer le point M pour que l'aire du triangle AMC soit
égal à 10? |
|
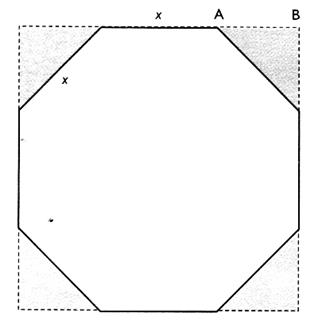
N°11 .
|
On veut découper dans une plaque carrée de a)
Sachant que chaque triangle hachuré est un
triangle rectangle isocèle , déterminé la mesure de chacun de leurs angles
aigus . b)
Calculer la longueur AB en fonction de "x" , puis la
longueur "x". |
|
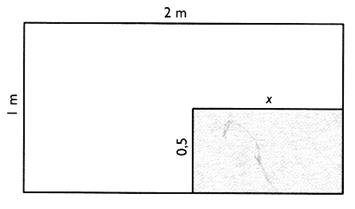
N°12
|
Dans une pièce rectangulaire de Donner l'expression de l'aire de la partie restante en fonction de
"x". Calculer "x" pour que l'aire de la partie restante soit |
|
|
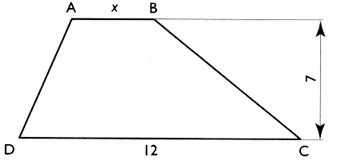
N°13
|
On considère un trapèze ABCD. Vérifier que l'aire du trapèze peut s'écrire :A = 8,5 x Calculer "x" pour que l'aire du trapèze soit égale à 172,2
cm² ( arrondie à deux décimales) |
|
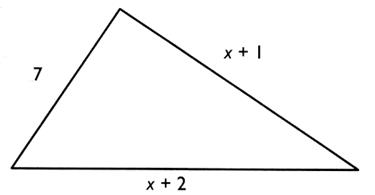
N° 14
|
Un triangle a les dimensions ( en m) indiquées sur la figure . Exprimer le périmètre du triangle en fonction de "x". Calculer "x" pour que le périmètre soit égal à |
|
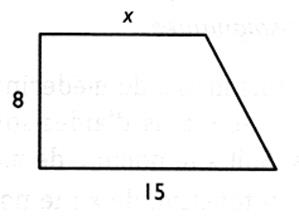
N°15
|
Montrer que l'expression de l'aire du trapèze rectangle en fonction de "x" est : A = 4 x + 60 Calculer "x" pour que l'aire du trapèze rectangle soit égale
à 200 cm² . Pour cela , résoudre l'équation : 4x + 60 = 200 |
|