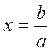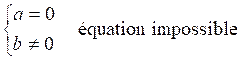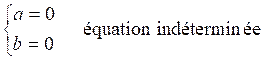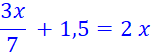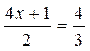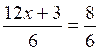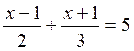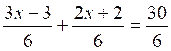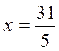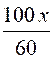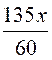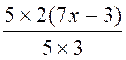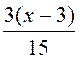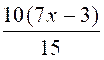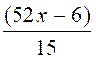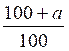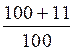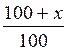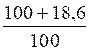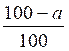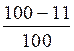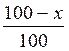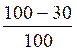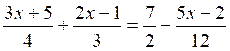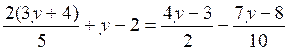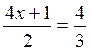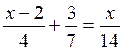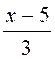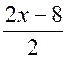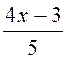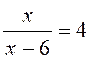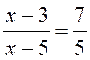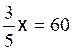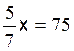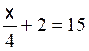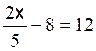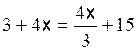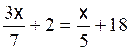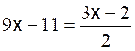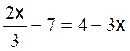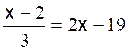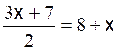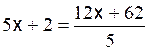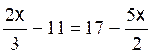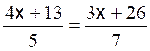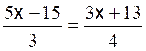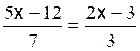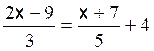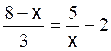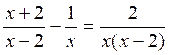|
CFA |
|
Pré requis:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Environnement du dossier :
|
1°)niveau V : le premier degré: exercices types et
problèmes (intro .) |
Objectif suivant: 2°) premier degré à deux
inconnues 3°) Inéquations du premier degré. |
DOSSIER : Résolution d'une Équation du premier degré à une
inconnue.
|
|
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
INFORMATIONS
|
|
|
|
|
I ) Définition : EQUATIONS DU PREMIER DEGRE A UNE INCONNUE.
EQUATION ENTIERE : En
faisant passer tous les termes dans un même membre , toute équation peut se
mettre sous la forme P = O
Si P est un polynôme , on dit que l’équation
est « entière » et le degré est le degré de l’équation.
Ainsi 3 x3
+ 5 x² - 4x + 3 = 3 x ( x² - 4x) +
5 est une équation du second degré
parce qu’elle est équivalente à :
17 x² - 4 x - 2 = 0
EQUATION DU PREMIER DEGRE.
D’après ce qui précède , une équation du premier
degré est une équation de la forme
P = 0
P étant un polynôme du
premier degré.
Si l’on fait passer tous les termes contenant
l’inconnue « x » dans le premier membre et tous les autres dans le
second, on obtient une équation de la forme :
(1) a x = b
« a » et « b » étant des données.
1°) si a
¹
0 , on peut
diviser les deux membres par « a ».On voit ainsi que l’équation (1)
admet une seule solution : 
2°)Si a = 0 l’équation (1) s ‘écrit : 0 × x = b
Or quel que soit « x », le premier membre
est nul . Donc si « b » est différent de zéro, l’équation n’admet
aucune solution. On dit qu’elle est impossible.
Si « b » est nul, quel que soit
« x », l’équation est toujours satisfaite. On dit qu’elle est indéterminée.
En résumé :
si a ¹ 0 solution
REMARQUE : Si l’équation
renferme des données littérales ( paramètres),on sera en général amené à
distinguer plusieurs cas car pour certaines valeurs des paramètres le
coefficient de l’inconnue pourra être nul et on n’aura pas le droit de diviser les deux membres de l’équation par ce
coefficient.
|
|
COURS
|
|
Les premières équations du
premier degré de base sont:
Commentaire : Toutes les transformations d’équations
doivent se ramener aux modèles « types »suivants ( il est donc nécessaire de savoir
reconnaître et résoudre les modèles proposés )
|
Exemples
d’équations |
Modèles types |
Solution(s) |
|
|
1 x
= 7 |
Evidemment x = 7 :1 |
a x =
b |
donc x =
b /a (x = 7) |
|
5 x =
45 |
a x =
b ou x a = b |
donc x =
b /a (x = 9) |
|
|
5 + x = 45 |
a + x = b ou x + a = b |
donc x = b -a (x = 40) |
|
|
5 - x = 45 |
a - x = b |
donc x = a -b (x = - 40) |
|
|
x - 5 = 45 |
x –a = b |
donc x = b +a (x = 50 ) |
|
|
|
|
donc x = (b a)
/c (x = 15) |
|
|
|
|
donc x =
a c / b (x = 5/3 ) |
|
|
|
|
donc
x = b a /c (x = 15 ) |
|
|
|
|
donc x = c a /b (x = 5 /3) |
|
|
|
|
donc x = b a (x = 40) |
|
|
|
|
donc x = a/b (x = 2,5 ) |
A savoir :Une équation du premier degré peut contenir dans chaque
membre 1 ou plusieurs termes :
Exemples : x +3 = 7 ; 2x +7
= 35 ; 3
x + 54 = -5x + 31 - 4
; 
+ (- 5) = 0 ; ….
ACTIVITES :
N°1 : Résoudre les équations d’inconnue « x ».
|
|
|
Corrigé : |
|
|
|
|
|
|
7x + 3 = 4x - 7
|
|
|
|
3 (4x - 2) = 5 (3 + x) |
|
Réponse : (x = 3) ;(x = - 10 / 3) ; (x = - 4)
N°2 : Trouver la solution
sans poser l’opération (mentalement)
|
Equations |
-4x - 12= 0 |
5x - 6 = 0 |
2x + 3 = 0 |
- 3 x + 4 = 0 |
|
Solution : |
|
|
|
|
Réponses : - 3 ; - 1,5 ; 4/3 ; 1,2
Fin de l’activité.
Pour résoudre une équation du premier degré à une
inconnue (possédant dans un membre plusieurs
termes ) ; on cherchera à ramener l’équation sous la
forme « a x = b »
Exemple 1 : Résoudre l’équation : 4 ( 2 x -3) + 7 - 6x =
5 - 3 ( 6 - 4x)
|
4 ( 2 x -3) + 7 - 6x - 5 + 3 ( 6 -
4x) = 0 |
|
|
8 x - 12 + 7 - 6 x - 5 + 18 - 12x = 0 |
|
|
- 10 x + 8 = 0 (forme
a x + b = 0 ; « a » = -10 et « b » = +8 ) |
|
|
Conclusion : Solution |
x = 0,8 |
Cas où il y a des dénominateurs :
Exemple 2 : Résoudre
l’équation
: 
+ 1,5
= 2 x
Procédure :
1° ) On effectue toutes
les simplifications visibles à priori :
Réduction de termes semblables @
|
|
|
|
|
|
|
|
|
|
|
|
|
2°) chasser les
dénominateurs, et les parenthèses s'il y en a , en effectuant les calculs
indiqués par ces parenthèses.
3° ) On fait ensuite passer dans un des membres de
l'équation tous les termes refermant l'inconnue et dans l'autre tous les termes
connus et l'on opère la réduction des termes semblables . si l'équation est
littérale on met l'inconnue en facteur commun.
(modèle obtenu après toutes ces transformations : ax = b )
4°) Enfin on
divise les deux membres de l'équation
par le coefficient de l'inconnue.
on dit aussi : on
divise le second membre par le coefficient
de "x" , le résultat est la solution cherchée (sous réserve de
la vérifier au cas où le dénominateur renfermait l'inconnue.
Procédure
permettant de chasser les dénominateurs:
|
On a à transformer
l'égalité
|
On veut une égalité équivalente:
|
On veut faire disparaître le dénominateur:
Il suffit de multiplier tous les termes par le nombre 7
|
|
Après calcul :on obtient l'égalité suivante: 3x + 10,5 = 14x |
+
Exemples de résolutions :
|
|
Résoudre : |
Résolution |
|
|
4,6 x = 18,4 |
x
= x = 4 Faire la
vérification : dans l’équation de départ il faut remplacer
« x » par la valeur proposée , et vérifier si l’égalité est
« vraie ». |
|
|
|
12 x + 3 = 8 x = Faire la
vérification : dans l’équation de départ il faut remplacer
« x » par la valeur proposée , et vérifier si l’égalité est
« vraie ». |
|
|
4 ( x -3) = 2 (
x-5)+3 |
4 x - 12
= 2x - 10 + 3 4 x -
2 x = 12 - 10 + 3 2 x = 5 x = Faire la
vérification : dans l’équation de départ il faut remplacer
« x » par la valeur proposée , et vérifier si l’égalité est
« vraie ». |
|
|
|
3x - 3 +2x +2 = 30 5x -1 = 30 5x = 31
Faire la
vérification : dans l’équation de départ il faut remplacer
« x » par la valeur proposée , et vérifier si l’égalité est
« vraie ». |
CAS GENERAL:
|
Exemple A
: |
|
|
|
Résoudre :
|
Il faut faire disparaître les dénominateurs ! |
|
|
1°) réduire au même dénominateur: calcul du PPDC de 2;3;5;4;20 = 60 |
Calcul du PPDC appelé aussi PPCM |
|
|
2°) Transformer tous les termes : l’égalité de départ devient l’égalité
équivalente :
|
Il faut Transformer l’égalité proposée par une égalité équivalente
dont tous les termes ont le même dénominateur !. |
|
|
3°) multiplier tous les termes par "60" ce qui revient à chasser le dénominateur
"60" : l’égalité : devient l’égalité équivalente : 90 x- 100x + 480 = 72x - 135 x +
639 |
||
|
4° )Réduire dans chaque membre: 1er
membre 90 x- 100x + 480 = x(90-100)+480
90 x- 100x + 480 = -10x +480 2ième
membre 72x - 135 x + 639 = x (72 -135 ) + 639 72x - 135 x + 639 = - 63x + 639 donc l’égalité : 90 x- 100x + 480 = 72x - 135 x
+ 639 devient l’égalité équivalente -10x +480 = - 63x + 639 |
||
|
On fait passer les "x" dans le premier membre et les
termes connus (nombres) dans le deuxième membre. *un terme change de membre change de signe : "voir égalité" -10x +480 = - 63x + 639 devient l'égalité : -10x +63x = 639 -480 |
||
|
On réduit : -10x +63x = 639 -480 devient :
53x = 159 |
|
|
|
Divisons les deux membres par "53": x= |
|
|
|
Conclusion x = 3 Vérification : On remplace dans le premier membre «
x » par la valeur « 3 » : Et l’on calcule : On remplace dans le deuxième membre «
x » par la valeur « 3 » : Et l’on calcule :
3,6 – 6,75 + 10,65 = 7,5 Si les deux nombres sont égaux alors « x =
3 » est la solution !.
ainsi : 7,5
=7,5 ; on peut confirmer que « x = 3 »est la solution ! |
||
|
Exemple B |
|
|
|
|
|
1°) réduire
au même dénominateur: calcul du PPDC de;3;5;15 ; = 15 |
|
|
2°) Transformer tous les termes
|
|
|
|
|
|
On multiplie tous les termes par "15": Ce qui revient à supprimer les dénominateurs. 3(x-3) + 120 =
10(7x-3 ) - (52 x -6) |
|
|
Suppression de parenthèses: 3x - 9 + 120 = 70x-30
- 52 x + 6 |
SOS développer |
|
Faisons passer tous les termes
en "x" dans le deuxième membre et les termes connus dans le premier
membre. -9 + 120 + 30 - 6 =
70x -52 x -3x 135 = 15 x |
SOS Factoriser 70x -52 x -3x x ( 70 -52 -3 ) = 15x |
|
Conclusion :
x = |
|
Activités : Exercices : (@ en relation avec les pourcentages)
|
Trouver x = ? ( on dit
« résoudre ») |
||
|
x = |
|
x = |
|
x = |
|
x = |
|
2,45 = |
|
x = |
|
Calcul nécessitant une
ou des transformations : |
||
|
245 = |
|
x = |
|
168 = |
|
x = |
3500
x
|
Soit l’égalité
de la forme : |
y = ( |
|
|
Calculez : |
|
|
|
x = ( |
|
x = |
|
694,4 = ( |
|
x = |
|
1126,7 = ( |
|
x = |
|
Soit l’égalité
de la forme : |
y = ( |
|
|
Calculez : |
|
|
|
x = ( |
|
x = |
|
486,75 = ( |
|
x = |
|
626,5= ( |
|
x = |
EN RESUME , on retiendra la procédure
suivante ; pour :
Résoudre une équation du premier degré il faut :
|
CAS général (sans
exemple) |
|
|
|
|
Il faut faire disparaître les
dénominateurs ! |
|
|
1°) réduire au même dénominateur: |
Calcul du PPDC appelé aussi PPCM |
|
|
2°) Transformer tous
les termes :de l’égalité de départ en égalité
équivalente dont tous les termes ont le m^me dénominateur : |
Il faut Transformer l’égalité proposée par une
égalité équivalente dont tous les termes ont le même dénominateur !. |
|
|
3°) multiplier tous
les termes par le PPDC ce qui revient à
chasser le dénominateur |
Voir : les égalités
« théorèmes » Multiplier tous les
termes par le PPDC,pour neutraliser les dénominateurs |
|
|
4° ) Réduire dans chaque membre: |
||
|
On fait passer
les "x" dans le premier
membre et les termes connus (nombres) dans le deuxième membre. *un terme change de
membre change de signe : "voir
égalité" |
||
|
On réduit : |
|
|
|
On résout la forme
« ax = b » |
|
|
|
Conclusion x = b /a |
Vérification : On remplace dans le premier membre « x » par la valeur
« b / a » : On remplace dans le deuxième membre « x » par la valeur
« b /a » : Et l’on calcule : si les deux nombres sont égaux alors « x = b /a » est la
solution |
|
ACTIVITES 2 :
1°) Résoudre l’équation
d’inconnue « x » : 
Solution :
- on calcule le plus petit dénominateur commun : résultat « 12 »
- on multiplie tous les termes de l’équation par « 12 »:
Après simplification, on obtient l’équation : 3 (3x +5) + 4 (2x -1)
= 6 × 7 - (5x - 2)
- On développe ; on met sous la forme « …..= 0 » :
9x + 15 + 8x - 4 = 42 -5 x+ 2
et on réduit : 22x
= 33
Solution : x = 1,5
2°) Résoudre l’équation : 
Solution :
- on calcule le plus petit dénominateur commun : résultat « 10 »
- on multiplie tous les termes de l’équation par « 10 »:
Après simplification, on obtient l’équation : 4 (3y +4) + 10 (y -2)
= 5(4y-3) - (7y - 8)
- On développe ; on met sous la forme « …..= 0 » :
12y + 16 + 10y - 20 - 20y+15 + 7y-
8 = 0
et on réduit : 9y
+3 = 0
Solution : x = - (1/3)
Pour chaque cas « cliquer sur «
»
|
Equation type: ax = b
; 9 x
= 45 |
Savoir résoudre |
Electricité
|
|
|
Physique : |
|
|
Mécanique (poids et masse) |
|
|
Mouvement uniforme |
|
|
Travail d'une force |
|
|
Mouvement uniformément varié |
|
|
Equation type ax -b = c
; 5x -14 =16 |
Savoir résoudre |
|
Surface d'un triangle |
|
|
Calcul d'intérêt simple |
|
|
Densité d'un corps |
|
|
Equation type
|
|
|
Equilibre d'un levier |
|
|
Roues et engrenages |
|
|
Equilibre d'un treuil |
|
|
Chimie : |
|
Chimie :
L’atome : On donne l’écriture suivante : 1123
Na (qui symbolise l’atome de Sodium (natrium)), combien compte t- on de
neutrons ?
Donner la procédure pour
résoudre une équation du premier degré , comportant des parenthèses et des
dénominateurs.
Devoir L le corrigé est dans le cours) Série 1 :
|
|
Résoudre : |
Résolution |
|
1-a |
4,6 x = 18,4 |
|
|
1-b |
|
|
|
1-c |
4 ( x -3) = 2 ( x-5)+3 |
|
|
1-d |
|
|
Série 2 :
|
|
Résoudre : |
Résolution |
|
1-a |
9x =
4,2 |
|
|
1-b |
7 x +
3,2 = 7,7 |
|
|
1-c |
3 ( 2x - 1) = 5 ( 6x + 4,2) |
|
|
1-d |
|
|
RESOUDRE LES
EQUATIONS SUIVANTES:
Série N° 1
|
5 x = 45 |
|
|
5+ x = 45 |
|
|
5 - x = 45 |
|
|
x -5 = 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Série N° 2
|
8x = 48 |
|
|
6x = 72 |
|
|
9x -7 = 20 |
|
|
4x +15 = 23 |
|
Série N° 3
|
5x - 60 = 0 |
|
|
40x - 25x = 75 |
|
|
16x -20 = 60 |
|
Série N° 4
|
|
|
|
5x = |
|
|
|
|
Série N° 5
Faire les calculs suivants : (en relation avec les pourcentages)
|
x = |
|
x = |
|
x = |
|
x = |
|
2,45 = |
|
x = |
|
Calcul nécessitant une
ou des transformations : |
||
|
245 = |
|
x = |
|
168 = |
|
x = |
|
Soit l’égalité
de la forme : |
y = ( |
|
|
Calculez : |
|
|
|
x = ( |
|
x = |
|
694,4 = ( |
|
x = |
|
1126,7 = ( |
|
x = |
|
Soit l’égalité
de la forme : |
y = ( |
|
|
Calculez : |
|
|
|
x = ( |
|
x = |
|
486,75 = ( |
|
x = |
|
626,5= ( |
|
x = |
Série N° 6
|
8x - 36 - ( 5x -4 ) = 20 - 10x |
|
|
6x - 2 ( x - 4 ) + (3x - 2 ) 15 = 468 |
|
Série N° 7
|
|
|
|
|
|
|
|
|
Série N°8 (corrigé dans le cours)
1°) Résoudre l’équation d’inconnue « x » :
2°) Résoudre
l’équation :
Série 9 : Résoudre les équations suivantes
|
|
|
Résultat |
|
|
|
Résultat |
|
5.
|
3x = 15 |
|
|
6.
|
90 - 13 x = 2x |
|
|
7.
|
8x = 120 |
|
|
8.
|
8x - 12 = 5x + 24 |
|
|
9.
|
2x = 17 |
|
|
10. |
3x + 15 = x + 35 |
|
|
11.
|
20x = 9 |
|
|
12. |
48 - 7x = 3x + 28 |
|
|
13.
|
3,2 x = 12 |
|
|
14. |
9x - 53 = 107 - x |
|
|
15.
|
|
|
|
16. |
54 x + 329 = 35x + 614 |
|
|
17.
|
|
|
|
18. |
12 x + 28 - 3x = 8x + 47 |
|
|
19.
|
5x = - 25 |
|
|
20.
|
2 ( 4x - 5) = 38 |
|
|
21.
|
- 3x = 42 |
|
|
22.
|
5x = 3 ( 4 - x) |
|
|
23.
|
- 7 x = - 35 |
|
|
24.
|
5 ( 39 - 3x ) = 3 ( 4x +2) |
|
|
25.
|
8x - 24 = 0 |
|
|
26.
|
7 ( 8x - 3) - 13 = 39 x |
|
|
27.
|
7 x- 63 = 0 |
|
|
28.
|
6x = 9 ( 18 - 4 x ) + 48 |
|
|
29.
|
- 4x - 44 = 0 |
|
|
30.
|
3x + 25 =4 ( 12 x - 5) |
|
|
31.
|
15 x + 75 = 0 |
|
|
32.
|
7x - 28 = 3 ( 24 - x) - 56 |
|
|
33.
|
12 x - 84 = 0 |
|
|
34.
|
120 - 7 ( 15 - 3x) = 4 ( 6x -2 ) - 10 |
|
|
35.
|
65 - 13 x = 0 |
|
|
36.
|
12x- 8 = 4x - ( 17 - x) |
|
|
37.
|
|
|
|
38.
|
|
|
Série 10 :
Résoudre.
|
|
|
Résultat |
|
|
|
Résultat |
||
|
39. |
|
|
|
40.
|
|
|
||
|
41.
|
|
|
|
42.
|
|
|
||
|
43. |
|
|
|
44.
|
|
|
||
|
45. |
|
|
|
46.
|
|
|
||
|
47. |
|
|
|
48.
|
|
|
||
|
49. |
|
|
|
50.
|
|
|
||
|
51.
|
|
|
|
52.
|
|
|
||
Niveau BEP - BAC PROF :
1°) Résoudre et discuter
suivant les valeurs du paramètre
« m » représentant un nombre connu, l’équation : 2 ( m - 1)x - m ( x-1) = 2m +3
(corrigé dans
le cours)
2°) Résoudre
a) Exercice
n°1 : Résoudre l’équation 
b) Exercice
n°2 : Résoudre l’équation 
ACTIVITE Niveau 3e : (discipline
« géométrie » : @ les inégalités triangulaires)
Données :
ABC est un triangle dont les côtés ont
pour mesure ( en cm).*
AB = 3x ; BC = 6 ; CA =
2x+1
Dans lequel « x » représente un nombre strictement positif.
1°) faire la figure dans le cas
où « x » = 1,5
Placer [ BC ] ; puis AB
= « ……… » ;
CA = « …….. ».
2°) Pouvez- vous dessiner le triangle quand «x = 8 » ?
Commencer par calculer les
côtés : AB = …….. ; CA = ……..
2°) Déterminer les valeurs de « x » pour lesquelles le
triangle existe ( sans être aplati). Le triangle existe à condition que la
longueur de chaque côté soit strictement inférieure à la somme des longueurs
des deux autres côtés.
- AB < BC + CA se
traduit par 3x < 6 + 2x +1 ; en
transposant on obtient
3 x - 2x < 6 + 1 ; c’est à
dire « x <
…….»
- BC <CA + AB se traduit
par 6 < …………….. ; en transposant on obtient
6 - 1< 2x + 3x
; c’est à dire « 5 <
………. »
et en divisant les deux membres par « 5 » on
obtient : ………
< x
- AC < AB + BC se traduit
par 2x +1 < …………….
; en transposant on obtient
1 - 6 < ……….. ;
c’est à dire « - 5 < x »
Ce qui est toujours vérifié puisque « x » est positif par
hypothèse.
-
En définitive le triangle existe quand 1 < x et x > 7 c’est à dire …..…..
< x
< ……
4°) Pour quelle valeur de « x »le périmètre du triangle est-il
égal à 32 cm ?
5°) Pour quelle valeur de « x », le triangle est -il
isocèle ?
- de base [ BC] ; AB = CA
- de base [ BC]
6°)
- Pour quelle valeur de « x » ; CA = 2 AB ?
- Pour quelle valeur de « x », CA = 2 BC ?
-
Pour quelle valeur de « x » ; CA = 
AB ?
7°) Se peut -il que le double de AB soit égal au triple de AC diminué de la
moitié de BC ?
CORRIGE Série 2 :
Série 2 :
|
|
Résoudre : |
Résolution
|
|
1-a |
9x = 4,2 |
X = 7/15 |
|
1-b |
7 x + 3,2 = 7,7 |
X= 9 / 14 |
|
1-c |
3 ( 2x -
1) = 5 ( 6x + 4,2) |
X = -1 |
|
1-d |
|
X = 0,4 |
Corrige :On donne l’écriture suivante : 1123
Na (qui symbolise l’atome de Sodium (natrium)), combien compte t- on de
neutrons ?
. « 23 » : représente la
somme de protons ( p ) et de
neutrons ( n ) ; ainsi 23 = p +
n ; puisque « p = 11 » ;
23 = p + n devient 23 = 11 + n ; on en déduit par calcul que n = 23
–11 soit n = 12 .
Conclusion,
l’atome de sodium a 11 électrons en périphérie ; son noyau possède 11 protons et 12 neutrons.