|
|
|
|
Les suites
géométriques |
|
|
Les puissances de
dix |
ENVIRONNEMENT du
dossier:
|
Objectif
précédent : |
1°) Les logarithmes (généralités ;
systèmes..) |
tableau |
DOSSIER : Le logarithme (découverte et notions : la septième opération)
1.
La septième
opération : La recherche de
l’exposant ;appelée : calcul du logarithme.
(exemple)
2. Découverte
et Définition : On dit que chaque terme de la
progression arithmétique est
« le logarithme » du
terme de même rang de la progression géométrique …….Ainsi :
|
TEST |
COURS
|
Interdisciplinarité |
|
COURS.
1
- La septième opération : La recherche de l’exposant ;appelée : calcul du logarithme.
a) Les
sept opérations en mathématique .
Nous savons que :
·
l’addition
(dit : la première opération) admet une opération inverse : la soustraction.(dit :
la deuxième opération)
·
La multiplication (dit : la troisième
opération) admet une opération
inverse : la division. (dit la
quatrième opération)
·
La cinquième opération mathématique est l’élévation à une puissance ; celle-ci admet deux opérations
inverses :
Si 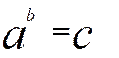
·
La recherche de « ![]() » est l’extraction de la racine :
dit : la
sixième opération.
» est l’extraction de la racine :
dit : la
sixième opération.
·
La recherche de
« b » est la septième opération. C’ est la recherche de la valeur de l’exposant : appelée : calcul du
logarithme.
Exemple :
Quelle
est la valeur de l’exposant qui a permit « ![]() « ; tel que :
« ; tel que : 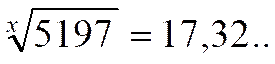 ;
; 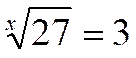
Découverte et
Définition : du système
de logarithmes.
ACTIVITE 1 :
A) Considérons deux progressions croissantes :
L’une « arithmétique » :
commençant par zéro .
on désigne par la lettre « r » la
raison de cette progression (arithmétique)
|
Termes classés par ordre croissant : |
0 |
r |
2r |
3r |
4r |
…………………………. |
nr |
|
|
1er terme |
2ème terme |
3ème terme |
4ème terme |
5ème terme |
|
nème terme |
L’autre : « géométrique » ;
commençant par 1 . on désigne
par la lettre « q »
|
Termes classés par ordre croissant : |
1 |
q |
q² |
q3 |
q4 |
…………………………. |
qn |
|
|
1er terme |
2ème terme |
3ème terme |
4ème terme |
5ème terme |
|
nème terme |
ACTIVITE 2 :
B) On
fait correspondre « terme à terme » les deux suites pour obtenir le tableau
suivant :
|
|
Rang 1 |
Rang 2 |
Rang 3 |
Rang 4 |
Rang 5 |
|
Rang « n » |
|
Termes classés par ordre croissant : |
0 |
r |
2r |
3r |
4r |
…………………………. |
nr |
|
|
1er terme |
2ème terme |
3ème terme |
4ème terme |
5ème terme |
|
nème terme |
|
Termes classés par ordre croissant : |
1 |
q |
q² |
q3 |
q4 |
…………………………. |
qn |
|
|
1er terme |
2ème terme |
3ème terme |
4ème terme |
5ème terme |
|
nème terme |
On lit ce tableau « verticalement) :
-au premier
terme 0 (de la suite arithmétique) on fait correspondre le premier terme 1 (de la
suite géométrique )
--au deuxième terme
« r » (de la suite arithmétique) on fait correspondre le deuxième terme
« q » (de la suite géométrique )
--au
troisième terme « 2r » (de la suite
arithmétique) on fait
correspondre le troisième terme
« q² » (de la suite géométrique ) ;
-…………………………………………………………………………..
--au n-nième terme « n » (de la suite
arithmétique) on fait
correspondre le nième terme « qn » (de la
suite géométrique )
ACTIVITE 3 : apparat ion du mot « logarithme »
« On
dit : »
|
Rang 1 |
Rang 2 |
Rang 3 |
Rang 4 |
Rang 5 |
|
Rang « n » |
|
0 |
r |
2r |
3r |
4r |
…………………………. |
nr |
|
|
|
|
|
|
|
|
|
1 |
q |
q² |
q3 |
q4 |
…………………………. |
qn |
On dit que chaque terme de la progression
arithmétique est « le
logarithme » du terme de même rang
de la progression géométrique ……
Ainsi :
«
0 » est le logarithme de
« 1 »
« r » est le
logarithme de « q »
« 2 r
» est le logarithme de
« q² »
« 3
r » est le logarithme de « q 3 »
« 4 r
» est le logarithme de « q 4 »
« n.r » est le
logarithme de « q n»
« Le système de logarithmes »
L’ensemble des deux progressions constitue un
système logarithmes.
La seule condition à réaliser pour constituer un
système de logarithmes est que la progression arithmétique commence par zéro et
que la progression géométrique commence par l’unité ; on en tire les
remarques suivantes :
ACTIVITE 4 : On
peut créer une infinité de systèmes logarithmes
on dit :
qu’il existe une
infinité de systèmes de logarithmes puisque la raison de chacune des
progressions est arbitraire :
Il suffit de fixer
une valeur pour « r »
et une valeur pour « q » pour obtenir un nouveau système de
logarithmes.( à vous d’en inventer un)
Exemple 1 : on pose : r = 1 ; q= 2
|
Rang 1 |
Rang 2 |
Rang 3 |
Rang 4 |
Rang 5 |
|
Rang « n » |
|
0 |
1 |
2r = 2x1 = 2 |
3r = 3x1 = 3 |
4 |
5 |
nr |
|
|
|
|
|
|
|
|
|
1 |
21 |
2 2 |
2 3 |
2 4 |
25 |
qn |
|
|
|
|
|
|
|
|
|
|
2 1 = 2 |
2 2 = 4 |
2 3 = 8 |
2 4=16 |
25 = 32 |
|
Dans le
système ce dessus : le
logarithme de 8
(23) est 3
; le logarithme de
32 (25 ) est
5 ; …………………… ;
Exemple 2 : on
pose « r » = 3 et
« q » = 3
|
Rang 1 |
Rang 2 |
Rang 3 |
Rang 4 |
Rang 5 |
|
Rang « n » |
|
0 |
3 |
2 x 3 = 6 |
9 |
12 |
15 |
3n |
|
|
|
|
|
|
|
|
|
1 |
31 |
3 2 |
3 3 |
3 4 |
35 |
3n |
|
|
|
|
|
|
|
|
|
|
3 |
9 |
27 |
81 |
243 |
|
Dans le
système ce dessus : le
logarithme de 27
(33) est 9
; le logarithme de
243 (3 5
) est 15 ;
…………………… ;
Exemple 3 :
on pose « r » = 1
et « q » = 10
|
Rang 1 |
Rang 2 |
Rang 3 |
Rang 4 |
Rang 5 |
|
Rang « n » |
|
0 |
1 |
2 |
3 |
4 |
5 |
1 x n |
|
|
|
|
|
|
|
|
|
1 |
101 |
10 2 |
10 3 |
10 4 |
10 5 |
10 n |
|
|
|
|
|
|
|
|
|
|
10 |
100 |
1 000 |
10 000 |
100 000 |
|
Dans le
système ce dessus : le
logarithme de 10
( 10 1 ) est
1 ; le logarithme de
100 (10 2 )
est 2 ; le logarithme de
1 000 ( 103 )
est 3 ;
le logarithme de 100
000 (10 5 )
est 5 ; …………………
…………………… ;
Est ainsi de suite …………voir Les
logarithmes (généralités ; systèmes..) ;
pour « base » d’un
système de logarithmes.
ACTIVITE : voir
Utilisation du logarithme pour extraire la racine d’un nombre .
TRAVAUX AUTO - FORMATIFS
EVALUATION
Exercice :
Effectuer la racine cubique de 5 197 ; noté : ![]()