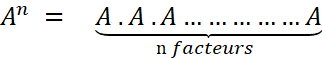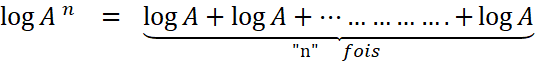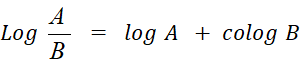Les suites de nombres et ensembles de nombres

2°) Les suites géométriques

1°) Les suites arithmétiques

Les puissances de dix

Index  warmaths

Objectif précédent :

 Notions sur le logarithme.

Objectif suivant :

1°)Les logarithmes de « x »

2°)la fonction log.

3°) la représentation graphique et l’échelle logarithmique.

4°) les logarithmes vulgaires

tableau     195

Liste des cours disponibles sur les logarithmes.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

I )   Etablissement d’un système logarithmique ……..

Considérons deux progressions croissantes , l’une géométrique ( G ) de raison « k » , l’autre arithmétique ( A) de raison   ( r ) et faisons correspondre les termes de  ( g ) et de  (A) de telle façon que l’unité dans la progression géométrique corresponde au zéro , dans la progression arithmétique.

( G )

…..

1

K

K²

K³

K⁴

……..

kⁿ

( A )

- nr

- 4 r

- 3 r

- 2 r

- r

0

r

2r

3r

4 r

…..

n r

On dit que les deux progressions forment un système de logarithmes et qu’un terme quelconque de la progression arithmétique  ( A ) est le logarithme du terme correspondant de la progression géométrique  ( G ) .

Ainsi :

           « - 4 r »  est le log de     :   soit    log  =  - 4 r

et 

            « 4 r »  est le log de K⁴     ; soit  log K⁴  = 4 r

Lorsque l’on examine  ce système de logarithmes . plusieurs remarques s’imposent immédiatement   :

1°) La progression  géométrique (G) ne peut avoir que des termes positifs , il en résulte que les nombres négatifs n’ont pas de logarithmes.

2°) Le logarithme de « 1 » est toujours « 0 »

3°) Les nombres supérieurs à « 1 »  ont un logarithme positif ; les nombres inférieurs à « 1 » ont un logarithme négatif.

4°) Le logarithme d’une puissance quelconque de « k » est égal au produit de « r » par l’exposant de cette puissance.

5°) Le logarithme de l’inverse d’un nombre et le logarithme de ce nombre ont des valeurs opposées :   log   =   - log k ⁿ

On conçoit qu’en choisissant  « k » suffisamment voisin de « 1 » et « r »    suffisamment voisin de « 0 » les progression arithmétique ( A)  et géométrique ( G ) seront telles que deux termes consécutifs différeront d’aussi peu qu’on le voudra .

Dans ces conditions il sera possible d’identifier exactement ou , avec une certaine approximation , n’importe quel nombre avec l’un des termes de la progression géométrique , son logarithme exact ou approché étant le terme correspondant de la progression arithmétique.,

Par définition : on appelle « base » d’un système de logarithme le nombre qui , dans un système a pour logarithme « 1 » .

II )  PROPRIETES  COMMUNES   à tous les systèmes de logarithmes ……

Les logarithmes jouissent des propriétés importantes grâce auxquelles ,  leur emploi est très utile dans le calcul numérique.

I ) Logarithme d’un produit.

1°) cas de deux facteurs :

Soit le produit :  A . B  

Identifions « A » et « B » avec des termes de même valeur de la progression géométrique ( G)

Soit  A = ( k^m ) ;  B  = ( k ⁿ )   

Nous avons :   Log A.B  =   Log ( k^m ) ( k ⁿ ) =   Log k ^m+n   =   ( m + n ) r    

=  ( m r ) + ( n r )

= Log ( k^m ) + Log  ( k ⁿ )

=  Log A + log B

2°)  Cas de trois facteurs.

Soit le produit : A . B . C

Nous avons :

Log A. B. C. 

= Log ( A . B ) C

= Log A.B + log C

= log A + log B + log C

Le même raisonnement étant valable pour un produit d’un nombre quelconque de facteurs , la propriété est générale et s’énonce .

Règle 1 : Le  logarithme d’un produit est égal à la somme des logarithmes des facteurs.

II ) le logarithme d’une puissance.

Soit 

Appliquons la règle (1)

Log A ⁿ   =  n log A

Règle 2 : Le logarithme d’une puissance  d’un nombre est égal au produit de ce nombre par l’exposant de la puissance.

III ) le logarithme d’une racine.

Soit    qui peut s’écrire     

Appliquons la règle   (  2 )

Log   =   log   =    log A

Règle 3 : le logarithme de la racine n^ième  d’un nombre est égal au quotient par « n » du logarithme de ce nombre.

IV ) le logarithme d’un  quotient.

Soit   qui peut s’écrire    A .

Appliquons la règle (1)

Log   =  Log A .    =    Log A  +   log    

Or le logarithme de l’inverse d’un nombre est appelé « cologarithme » de ce nombre d’où la règle .

Règle 4 :  Le logarithme d’un quotient est égal à la somme du logarithme du dividende et du cologarithme du diviseur.

Nota : Nous avons précédemment remarqué que le logarithme de l’inverse d’un nombre et le logarithme de ce nombre ont des valeurs opposées.

log   =   - log k ⁿ

soit    colog.  k ⁿ  =    - log k ⁿ

                                                                     les deux relations : 

Et                         

                                       Sont donc équivalentes , cependant, dans la pratique des calculs logarithmiques on remplace toujours la soustraction d’un logarithme par l’addition du cologarithme correspondant.