|
Pré requis: |
|
||||||||||
|
|
|||||||||||
|
Les Statistiques info |
|||||||||||
|
ENVIRONNEMENT du dossier: |
DOC 6 |
||||||||||
|
Objectif précédent : |
Objectif suivant : |
tableau : |
|||||||||
|
DOSSIER : Les représentations graphiques utilisées en statistique. I
) généralités. II)
les graphiques de base.( de distribution et de répartition). III
) Les graphiques à échelle
arithmétique. (cartésiens et polaires) IV)
les graphiques à échelle non arithmétique (logarithmique ;…) |
|||||||||||
|
TEST |
COURS |
Interdisciplinarité
|
|
||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
I ) GENERALITES : |
|
|||||||||||||||||||||||||||||||
|
1°) Rôle de la représentation graphique. Le graphique est
un mode d'expression qui permet
"visuellement" de
saisir et de mémoriser un certain
nombre d'informations . C'est pourquoi , lors de la présentation des
résultats statistiques et
complémentairement aux tableaux , on utilise souvent une représentation
graphique . Cette représentation graphique peut répondre à
deux types d'objectifs: a) Etre
un moyen de communication et permettre de véhiculer une information. C'est ainsi que certains graphiques figurent dans
des articles de magasines et journaux , dans des brochures de présentation de
résultats commerciaux ou (et)
comptables et même dans certaines
publicités . Ceci prouve qu'un bon
graphique est souvent plus explicite qu'un long discours. b) Etre un instrument de travail et permettre une vue d'ensemble synthétique du phénomène étudié , ce qui en
facilite l'analyse. (voir info plus !!!!) |
||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
2°) Typologie des graphiques. |
|
||||||||||||||||||||||||||||||
|
Selon J. Leurion : En matière statistique, tout graphique est caractérisé par : |
||||||||||||||||||||||||||||||||
|
|
a) La
nature de la série qu’il représente : |
|
||||||||||||||||||||||||||||||
|
|
- graphiques chronologiques. |
|
||||||||||||||||||||||||||||||
|
|
-
graphiques spatiaux,
quantitatifs ou qualitatifs |
|
||||||||||||||||||||||||||||||
|
|
b) Le système de coordonnées qu'il utilise : |
|
||||||||||||||||||||||||||||||
|
|
- coordonnées cartésiennes. |
|
||||||||||||||||||||||||||||||
|
|
- coordonnées polaires. |
|
||||||||||||||||||||||||||||||
|
|
-coordonnées pluri linéaires. |
|
||||||||||||||||||||||||||||||
|
|
c)
l'échelle retenue : |
|
||||||||||||||||||||||||||||||
|
|
-échelle arithmétique. |
|
||||||||||||||||||||||||||||||
|
|
-échelle logarithmique. |
|
||||||||||||||||||||||||||||||
|
|
-échelle fonctionnelle. |
|
||||||||||||||||||||||||||||||
|
|
(Voir INFO Plus !!!!) |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
3°) Construction des graphiques . D'une
façon générale, pour construire un graphique, certaines précautions
doivent être prises . a)
Déterminer les
intervalles de variation de la
variable pour en déduire l'échelle adéquate. b) Choisir l'intervalle- unité qui
permette de représenter correctement le phénomène et qui assure la meilleure utilisation de l'espace disponible. c)
Indiquer de façon
apparente le titre et la signification
des axes. En conclusion, il ne faut jamais oublier qu'un graphique, pour être utile,
doit se suffire à lui- même et dispenser le lecteur de toute référence à un autre document. |
|
|||||||||||||||||||||||||||||||
|
II )
GRAPHIQUES STATISTIQUES DE BASE : |
|
|||||||||||||||||||||||||||||||
|
Il existe deux sortes de graphique de base:
les graphiques de
distribution et les graphiques de répartition. |
|
|||||||||||||||||||||||||||||||
|
►A) Les graphique des
effectifs : (ces graphiques ont pour
fonction d’informer sur la distribution) Ce sont les
diagrammes à bâtons , les histogrammes et parfois des courbes , ils sont
utilisés pour représenter graphiquement
des effectifs simples ( valeurs données ou recueillies) simples et des fréquences simples ( valeurs
calculées) ►B) Les graphiques de fréquences
cumulées : (dont leur fonction est d’informer sur la répartition) Ce
sont les graphiques en escalier ou des
courbes « cumulatives » , ils informent graphiquement sur les
fréquences cumulées . ( valeurs calculées)
. |
|
|||||||||||||||||||||||||||||||
|
|
A) Graphiques des effectifs : ( on
distinguera deux cas : lorsque la variable statistique est discontinue
et lorsque la variable statistique est continue) |
|
||||||||||||||||||||||||||||||
|
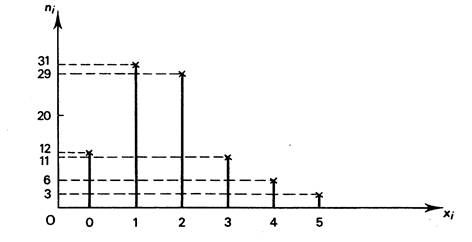
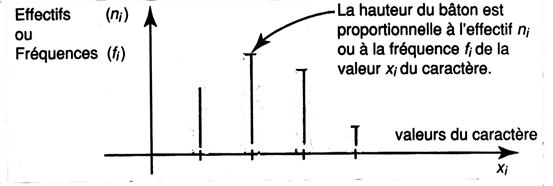
1°) Diagramme à bâtons pour le cas d’une variable
discontinue (ou discrète) : La représentation graphique des effectifs d’une
variable (ou caractère) discret s’effectuera sous la forme d’ un graphique en
bâtons. La valeur observée (recueillie ou donnée) du
caractère (ou « variable ») est portée sur l’axe des
« x » (abscisses) et
l’effectif (valeur recensée) correspondant sera portée sur l’axe des
« y » (axe perpendiculaire à l’axe Ox ) appelé « axe des
ordonnées » ou « axe des n » L’axe des abscisses sera l’axe des « xi » et l’axe des ordonnées sera l’axe des « fi ». Le « bâton » est le segment de droite
perpendiculaire à l’axe des Ox , dont la hauteur ( ou sa longueur ) est
proportionnelle à l’effectif correspondant. Exemple : la série statistique ci dessous
représenté par le diagramme en bâtons , informe sur la façon dont se
distribue le personnel (foyer) d’une
entreprise en fonction du nombre d’enfants. |
||||||||||||||||||||||||||||||||
|
|
Nombre d’enfants par foyer « xi » |
Nombre de foyer concernés fi |
||||||||||||||||||||||||||||||
|
0 |
12 |
|||||||||||||||||||||||||||||||
|
1 |
31 |
|||||||||||||||||||||||||||||||
|
2 |
29 |
|||||||||||||||||||||||||||||||
|
3 |
11 |
|||||||||||||||||||||||||||||||
|
4 |
6 |
|||||||||||||||||||||||||||||||
|
5 |
3 |
|||||||||||||||||||||||||||||||
|
Remarque importante : Dans le cas d’une variable (caractère) discrète , il ne faut
pas joindre les sommets de bâtons car , par définition, il n’existe pas de valeur
intermédiaire entre deux positions de la variable ( caractère) |
||||||||||||||||||||||||||||||||
|
2°) L’histogramme : Cas d’une variable (
caractère) continue. La représentation graphique des effectifs d’une variable
continue est appelé un histogramme. |
|
|||||||||||||||||||||||||||||||
|
|
On portera
en abscisses les valeurs des classes des caractères (variables) , et
l’on portera en ordonnées les effectifs correspondants , on dit que l’on
représente la « structure de la population étudiée ». |
|
||||||||||||||||||||||||||||||
|
|
Pré requis Lycée : au
collège il faut savoir calculer l’aire des rectangles , après avoir relevé
les dimensions de ces rectangles sur le dessin. Et savoir présenter tous ces
calculs en vue de leur exploitation. |
|
||||||||||||||||||||||||||||||
|
Principe de construction de l’histogramme. Pour chaque classe , on élève un rectangle ayant une
base proportionnelle à l’intervalle de classe et une hauteur proportionnelle
à l’ effectif simple. Dans ce cas, ce sont les « surfaces » , et
non les hauteurs , qui « sont proportionnelles à l’effectif ». Dans la pratique, cependant, deux cas peuvent se
présenter. Le cas où les classes sont d’égales
amplitudes et le cas ou les amplitudes sont inégales. |
|
|||||||||||||||||||||||||||||||
|
|
Cas 1 : Classes sont d’égales amplitudes. |
|
||||||||||||||||||||||||||||||
|
|
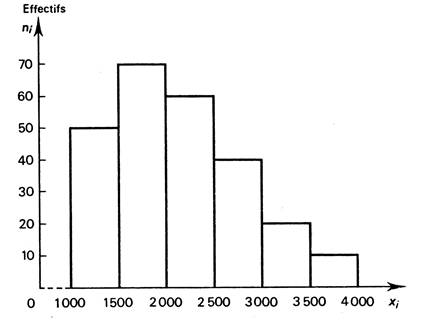
Exemples : distribution des salaires de
bases mensuels du personnel d’une société. |
|
||||||||||||||||||||||||||||||
|
Histogramme des
salaires mensuels en euros : |
|
|||||||||||||||||||||||||||||||
|
|
Salaire en € : x i |
Effectifs
ni |
||||||||||||||||||||||||||||||
|
1000 à 1500 |
50 |
|||||||||||||||||||||||||||||||
|
1501 à 2000 |
70 |
|||||||||||||||||||||||||||||||
|
2001 à 2500 |
60 |
|||||||||||||||||||||||||||||||
|
2501 à 3000 |
40 |
|||||||||||||||||||||||||||||||
|
3001 à 3500 |
20 |
|||||||||||||||||||||||||||||||
|
3501 à 4000 |
10 |
|||||||||||||||||||||||||||||||
|
|
250 |
|||||||||||||||||||||||||||||||
|
Remarque :
l’histogramme est constitué par l’ensemble des rectangles adjacents. Nous pouvons , par exemple, vérifier que le rectangle
représentatif de la classe [2501 ; 3000] ( effectif
« 40 ») a une surface une
fois et demi (1,5) plus grande
que celle du rectangle représentatif
de la classe 3001 à 3500 ( effectif « 10 ») Nous pouvons vérifier que le rapport des
effectifs pour 2 classes (pris au hasard ) et le
rapport des surfaces de ces rectangles correspondants sont égaux. Par exemple : Ainsi prenons deux classes : 2501 à 3000 et
3001 à 3500 : Rapport des effectifs : On remarque,si besoin était, que toutes les
surfaces sont proportionnelles entre elles en même temps que leur rapports
des effectifs correspondants sont égaux. (pour certifier la
validité de l’histogramme il faudrait comparer les classes entres
elles) . Ce qui n’est pas nécessaire si les classes ont la même amplitude . |
||||||||||||||||||||||||||||||||
|
|
Cas 2 : les classes d’une série sont d’amplitudes inégales. |
|
||||||||||||||||||||||||||||||
|
|
Pour respecter la proportionnalité des surfaces,
il va falloir, dans ce cas,
« rectifier » , en conséquence, les hauteurs. |
|
||||||||||||||||||||||||||||||
|
|
Supposons que l’on nous demande d’observer
la distribution précédente sur une
période de deux années. ( l’entreprise est en expansion……) |
|
||||||||||||||||||||||||||||||
|
|
On considère les classes suivantes : 1000 à
1500 ; 1501 à 2000 ; 2001 à 2500 ;2501 à 3500 ; 3501 à
4000 ; 4001 à 4500 . Les données sont ci contre : |
Salaire en € : x i |
Effectifs
ni |
|
||||||||||||||||||||||||||||
|
1000 à 1500 |
30 |
|||||||||||||||||||||||||||||||
|
1501 à 2000 |
90 |
|||||||||||||||||||||||||||||||
|
2001 à 2500 |
120 |
|||||||||||||||||||||||||||||||
|
2501 à 3500 |
180 |
|||||||||||||||||||||||||||||||
|
3501 à 4000 |
60 |
|||||||||||||||||||||||||||||||
|
4001 à 4500 |
30 |
|||||||||||||||||||||||||||||||
|
|
250 |
|||||||||||||||||||||||||||||||
|
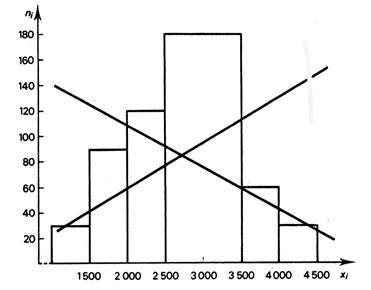
L’histogramme ci contre , tracer à partir des
données « telles quelles » est faux !! En effet, l’intervalle pour la classe 2501 à 3500
est double des autres , ce qui se traduit , si on ne modifie pas les
fréquences, par un manque de proportionnalité entre les surfaces. |
|
|
||||||||||||||||||||||||||||||
|
|
Pour le montrer : on va comparer le résultat
des deux rapports : effectifs et aires pour deux classes (prises
judicieusement).) A) on calcule
le rapport d’effectifs entre la classe 2501 à 3500 ( effectif 180) et la classe (par exemple) 3501 à 4000 (effectif 60 ) : le rapport est égal
à B) on calcule le rapport des surfaces pour ces deux
intervalles : 1°)calcul de
aire du rectangle de la classe [2501 ; 3500] 2°)Calcul de l’aire de la classe [3501 ;
4000]) 3°) division : 675 mm²
/ 112 , 5 mm² = 6 On compare
« 3 » et « 6 » et l’on constate que les rapports
ne sont pas égaux :On en conclut que l’histogramme est faux . Il ne
respecte pas les proportionnalité. Décision : l’histogramme est faux , il faut
modifier un paramètre pour
obtenir à un histogramme
« bon » |
|
||||||||||||||||||||||||||||||
|
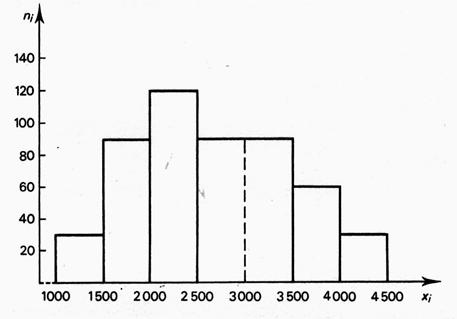
SOLUTION : On va rendre les classes égales. On remarque que
l’amplitude de la classe [2501 ; 3500] est le double des autres classes. Avant de refaire la représentation
graphique on va diviser par « 2 » le fréquence correspondant à
cette classe. On passera remplacera la classe [2501 ; 3500] par les
classes [2501 ; 3000] et [3001 ; 3500] . , et l’on limitera
l’effectif de ces classes au même nombre , en divisant l’effectif de la
classe [2501 ; 3500] par deux : : 180 / 2 = 90 . Remarque : si l’amplitude était plus que les
autres on rectifierait les effectifs par une multiplication. Ce qui nous donne l’histogramme
« correct » ci dessous : |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
Remarque : le segment en pointillé indique
la transformation effectuée et met en garde le lecteur sur le caractère
« relatif » des effectifs répartis entre les classes 2501 à 3000 et
3001 à 3500 . En effet , si l’on reprend la série statistique qui a servi de
base de départ du tableau , on pourrait trouver , par exemple un effectif
de 100
pour la classe 2502 à 3000 et de 80
pour la classe 3001 et 3500 .
Dans l’ignorance , ou le manque de précision , la répartition se fait
« égalitairement ». |
||||||||||||||||||||||||||||||||
|
|
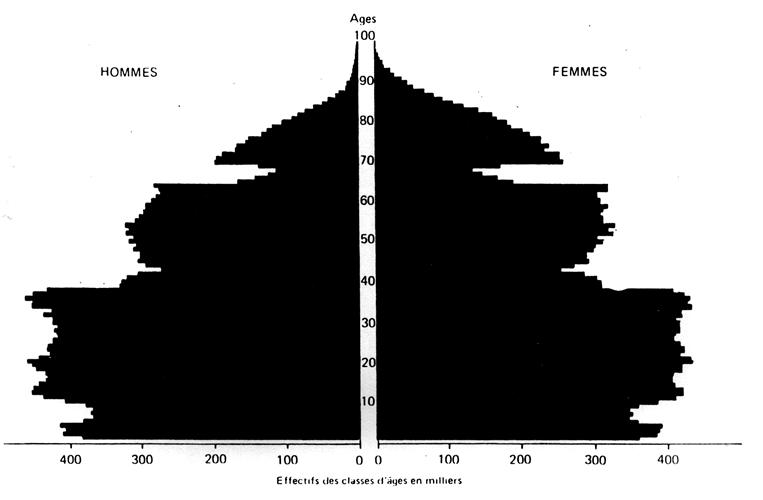
Cas particulier : La pyramide des
ages : |
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
Nous venons d’étudier l’histogramme , c’est en
partant des valeurs centrales des classes et de l’histogramme qu’il est
possible de tracer le polygone. trave. B) Le polygone des effectifs ou des
fréquences : |
|
||||||||||||||||||||||||||||||
|
|
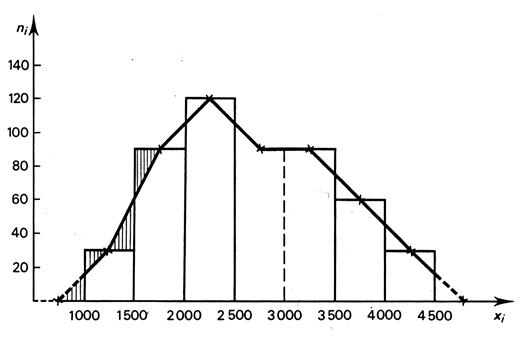
Le polygone des effectifs est obtenu en
joignant par des segments de droite
les milieux des bases supérieures des rectangles ,. Il permet de rendre
compte de la continuité du caractère (ou variable). Voir le
graphique ci dessous. |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Remarques : 1) l’aire de l’histogramme est égale à l’aire du
polygone Cette aire est égale , en prenant l’intervalle de
classe comme unité (sur l’axe des abscisses. Pour le polygone des effectifs : on prendra
la somme total des effectifs sur l’axe
des ordonnées. Pour le polygone des fréquences : on
prendra la somme des fréquences (
généralement = à 1) que l’on placera sur l’axe des ordonnées. |
|
||||||||||||||||||||||||||||||
|
|
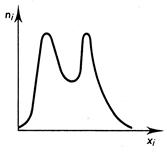
2) il arrive parfois qu’un histogramme présente
des « anomalies » sous forme de « puits » (faible
effectif dans une classe) ou de « cheminée ».(effectif important
dans une classe. ). On s’assurera qu’il ne s’agit pas d’erreurs et il faudra
rechercher l’explication de phénomène « a priori » singulier. Ces phénomène de « puit » ou de
« cheminée » sont souvent rencontrés sur des série statistiques
d’un magasin dont on analyse les prix affichés . On trouvera peut de prix
dans un intervalle de prix alors que l’on trouvera une grande quantité de
prix dans un autre intervalle. |
|
||||||||||||||||||||||||||||||
|
|
C) on vient de voir le polygone des effectifs ou
des fréquences. Mais on peut aussi rencontrer les « Courbes des
effectifs ou des fréquences ». |
|
||||||||||||||||||||||||||||||
|
|
Courbes des effectifs ou des fréquences : |
|
||||||||||||||||||||||||||||||
|
|
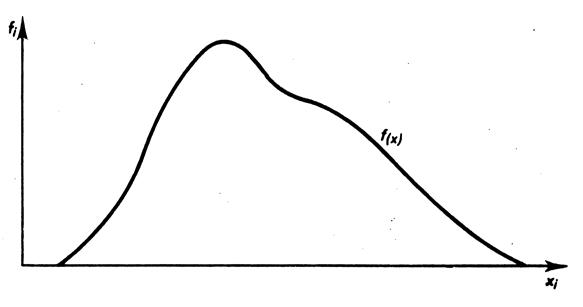
Lorsque l’intervalle des classes est très petit
et les données suffisamment nombreuses, la ligne brisée du polygone tend à devenir
une courbe appelée « courbes des fréquences » ou « courbes des
effectifs ». |
|
||||||||||||||||||||||||||||||
|
|
Remarque :lorsqu’il s’agit de fréquence , o, note cette
fonction : f ( x) . |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
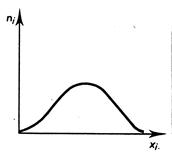
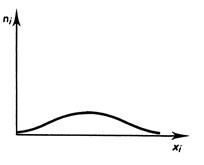
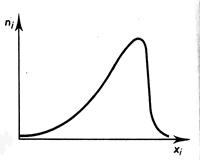
Etudes visuelles sur l’allure de la courbe
concernant la distribution : la plupart
des phénomènes rencontrés dans la réalité peuvent être illustrés par l’un des
6 cas de figure suivants. |
|
||||||||||||||||||||||||||||||
|
|
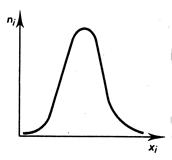
Distributions symétriques : on constate une |
|
||||||||||||||||||||||||||||||
|
Grande dispersion. |
Moyenne dispersion |
Petite dispersion |
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
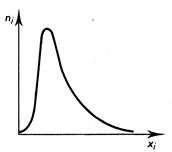
On
trouvera des distributions asymétriques |
|
|||||||||||||||||||||||||||||||
|
Courbe oblique à gauche. |
Courbe oblique à gauche. |
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
Dans les graphiques de base on rencontre aussi
les graphiques qui portent sur la répartition ce sont les : |
||||||||||||||||||||||||||||||||
|
|
Graphiques de fréquences cumulées |
|||||||||||||||||||||||||||||||
|
On trouvera deux cas : Le cas où la variable ( caractère) est
discontinue (représentée par un graphique « en escalier » croissant ou décroissant), et
le cas où la variable ( caractère) est
continue. (représentée par une courbe soit croissante ou soit
décroissante) |
||||||||||||||||||||||||||||||||
|
|
Cas A : Graphique représentant d’une série
statistique à caractère discontinu : |
|
||||||||||||||||||||||||||||||
|
|
La représentation graphique des Fréquences
Cumulées ( FC) d’une variable discrète
s’effectue sous la forme d’un graphique en escalier. Les « sauts » correspondent aux valeurs
possibles de la variable et sont égaux aux « Fréquences Cumulées
Croissantes ou Décroissantes. ( FCC ou FCD). On notera : « Effectifs Cumulés Croissants ou Décroissants. ( ECC
ou ECD). |
|
||||||||||||||||||||||||||||||
|
|
Exemple : 1997 : On a fait un sondage
auprès des 89 foyers d’une citée, on veut étudier la répartition des foyers en fonction du nombre d’écran (
téléviseur ou ordinateur) par foyer. |
|
||||||||||||||||||||||||||||||
|
xi |
Effectifs n i |
Fréquences f i |
||||||||||||||||||||||||||||||
|
|
simple |
ECC |
ECD |
simple |
FCC |
FCD |
||||||||||||||||||||||||||
|
0 |
12 |
12 |
89 |
0,135 |
0,135 |
1 |
||||||||||||||||||||||||||
|
1 |
31 |
43 |
77 |
0,348 |
0,483 |
0,865 |
||||||||||||||||||||||||||
|
2 |
29 |
72 |
46 |
0,326 |
0,809 |
0,517 |
||||||||||||||||||||||||||
|
3 |
11 |
83 |
17 |
0,124 |
0,936 |
0,191 |
||||||||||||||||||||||||||
|
4 |
4 |
87 |
6 |
0,045 |
0,977 |
0,067 |
||||||||||||||||||||||||||
|
5 |
2 |
89 |
2 |
0,022 |
1 |
0,022 |
||||||||||||||||||||||||||
|
total |
89 |
|
|
1 |
|
|
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
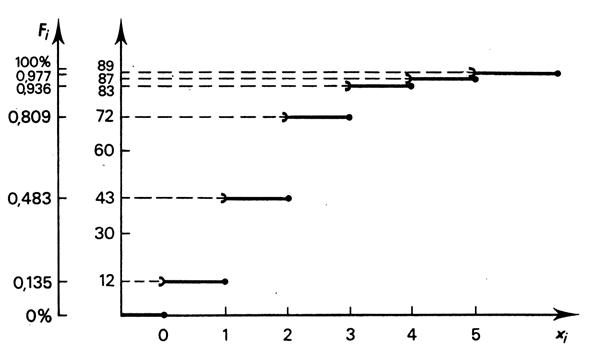
Le
graphique ci - dessous montre la répartition croissante. La lecture de
ce graphique permet d’identifier la répartition ( absolue ou relative) des
foyers ayant « x écrans ou moins » .exemple : 72 foyers
possèdent ( ou 80,9 %) au 2 écrans
ou moins. |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
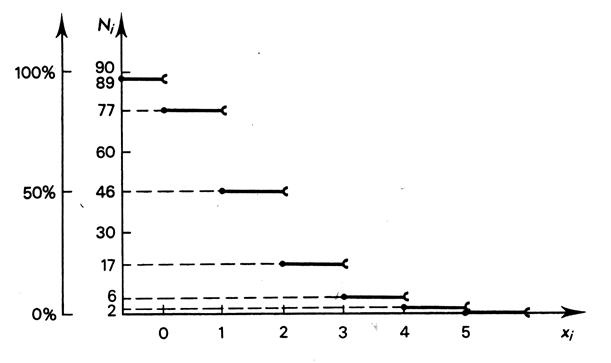
|
Répartition décroissante : (voir le tableau
ci dessous) :Ici les résultats sont inversés, à savoir « les foyers possèdent « x »
écrans ou plus . |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
On remarquera , par exemple , que 46 foyers (
soit 51,7%) possèdent 2 écrans ou plus. |
|
||||||||||||||||||||||||||||||
|
Remarque : Lorsqu’il s’agit de fréquences cumulées , on note
cette fonction : F (x). Cette dernière est nulle pour les valeurs de « x »
inférieures à la plus petite valeur « x1 » et égal a
« 1 » pour les valeurs de « x » supérieures à la plus
grande valeur possible « xk » (ceci pour les fréquences
cumulées croissantes. Les fréquences cumulées décroissantes donnent,
évidemment, des résultats inversés . |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Cas B : Graphique représentant d’une série
statistique à caractère continu : (c’est aussi
un graphique de répartition) |
|
||||||||||||||||||||||||||||||
|
|
Les fréquences cumulées ( FC) sont aussi soit
cumulées croissantes soit cumulées décroissantes. |
|
||||||||||||||||||||||||||||||
|
|
►Courbe des fréquences cumulées croissantes : elle se construit en
portant les points correspondant à chaque classe à la limite
« supérieure » de l’intervalle de classe. Nota : la présence de classes d’amplitudes
inégales n’entraîne aucune modification en ce qui concerne la construction de
cette courbe., ►Courbe des fréquences cumulées décroissantes : elle se construit
en portant les points correspondant à chaque classe à la limite
« inférieure » de l’intervalle de classe. |
|
||||||||||||||||||||||||||||||
|
|
Exemple :
soit le tableau suivant : |
|
||||||||||||||||||||||||||||||
|
|
xi |
Effectifs ni |
|
|||||||||||||||||||||||||||||
|
|
Simple |
ECC |
ECD |
|||||||||||||||||||||||||||||
|
] 10 ; 15 ] |
3 |
3 |
52 |
|||||||||||||||||||||||||||||
|
] 15 ; 20 ] |
9 |
12 |
49 |
|||||||||||||||||||||||||||||
|
] 20 ; 25 ] |
12 |
24 |
40 |
|||||||||||||||||||||||||||||
|
]
25 ; 35 ] |
18 |
42 |
28 |
|||||||||||||||||||||||||||||
|
] 35 ; 40 ] |
6 |
48 |
10 |
|||||||||||||||||||||||||||||
|
] 40 ; 45 ] |
3 |
51 |
4 |
|||||||||||||||||||||||||||||
|
] 45 ; 50 ] |
1 |
52 |
1 |
|||||||||||||||||||||||||||||
|
|
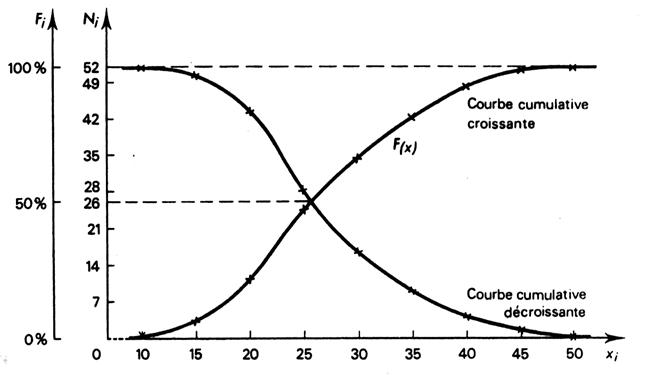
Il se traduit par les deux courbes
suivantes : |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
On contrôlera l’exactitude du graphique en
vérifiant que l’intersection des deux courbes a pour ordonnée la moitié de
l’effectif. La courbe cumulative croissante est aussi appelée
« fonction cumulative croissante F (x) et elle est toujours monotone croissante. De même : La courbe cumulative décroissante est aussi
appelée « fonction cumulative croissante F (x) et elle est toujours monotone décroissante. |
||||||||||||||||||||||||||||||||
|
|
III )
GRAPHIQUES A ECHELLE ARITHMETIQUE ( ils sont au nombre de trois : à
coordonnées cartésiennes , à coordonnées polaires , et le graphique à
secteurs circulaires). |
|
||||||||||||||||||||||||||||||
|
1°) Les graphiques à coordonnées cartésiennes |
|
|||||||||||||||||||||||||||||||
|
|
Les graphiques chronologiques. Comme leur nom l’indique, ces graphiques
renseignent sur l’évolution d’une série
chronologique . Les périodes de temps sont portées sur l’axe des
abscisses et les valeurs de la variable (caractère) sont portée en ordonnées.
Remarquer que nous n’avons donc pas ici de fréquence. |
|
||||||||||||||||||||||||||||||
|
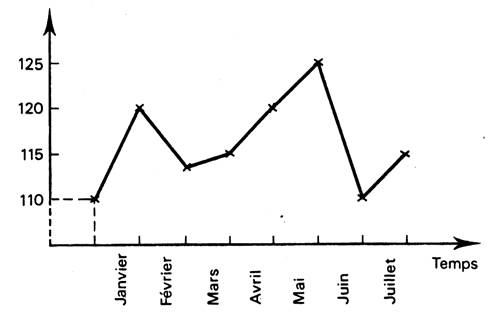
Exemple 1 : relevé du stock
des marchandises « A » le 1er de chaque mois. Dans le cas de série chronologiques
représentative d’un niveau de stock, chaque observation est noté
perpendiculairement à la date correspondante. En ordonnée :les unités représentant de la
grandeur . |
|
|||||||||||||||||||||||||||||||
|
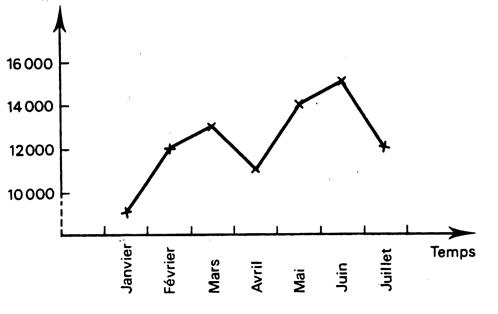
Exemple 2 : dans le cas
de séries chronologiques se rapportant à des flux, chaque observation est
portée sur la perpendiculaire du milieu de la période. Voir le tableau ci contre représentant un relevé d’un
chiffre d’affaires mensuel. En ordonnée, le chiffres d’affaire en milliers
d’euros. |
|
|||||||||||||||||||||||||||||||
|
Remarque : les graphiques chronologiques
permettent d’apprécier une observation récente ou de prévoir l’évolution à
court terme d’un phénomène. Des méthodes dites « d’ajustement »
mettent en évidence les tendances profondes d’un phénomène, en éliminant, par
exemple, les variations saisonnières des observations. |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
1°) Les graphiques à coordonnées
polaires : ( voir repérage d’un point) |
|
|||||||||||||||||||||||||||||||
|
|
( on trouvera deux modèles : graphique polaire
et graphique à secteurs) |
|
||||||||||||||||||||||||||||||
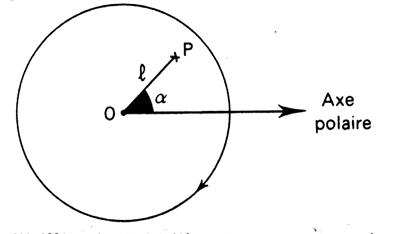
|
Dans ce type de graphique , un point est
répété au moyen de l’angle « a » et de la longueur « l » du segment OP. En application de ce principe, on utilise couramment
en statistiques les deux graphiques suivants. |
|
|||||||||||||||||||||||||||||||
|
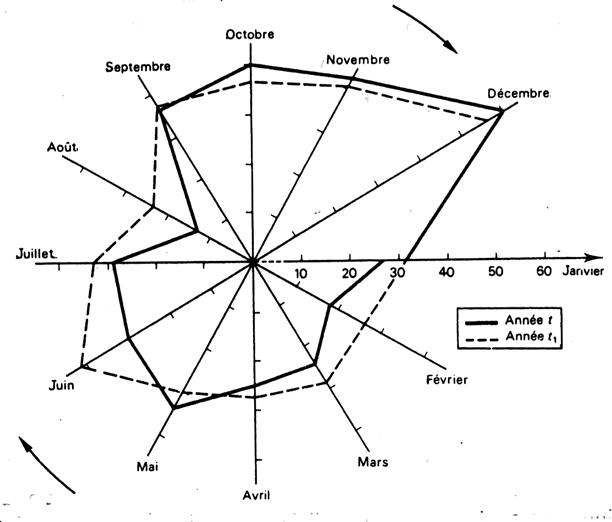
a) 1 : graphique polaire. Il est très utilisé
pour les séries chronologiques, ce graphique est une représentation dans laquelle
le temps s’écoule d’une manière circulaire et dans le sens des aiguilles
d’une montre. Un vecteur polaire
représente une unité de temps pré- déterminée ( un mois , un trimestre , un
semestre, etc….) |
||||||||||||||||||||||||||||||||
|
Exemple : évolution du
chiffre d’affaires d’un grand magasin ( en milliers d’euros) |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
Nous sommes partis du tableau suivant : |
|
||||||||||||||||||||||||||||||
|
|
j |
f |
m |
a |
m |
j |
j |
a |
s |
o |
n |
d |
||||||||||||||||||||
|
Année t |
27 |
18 |
24 |
25 |
33 |
30 |
28 |
12 |
36 |
41 |
43 |
60 |
||||||||||||||||||||
|
Année t1 |
31 |
21 |
29 |
27 |
31 |
41 |
32 |
22 |
37 |
36 |
41 |
56 |
||||||||||||||||||||
|
Le mois étant l’unité de temps, l’angle formé par deux segments
consécutifs est de ( 400 gr./ 12 = 33,33 gr) ou 360 ° / 12 = 30°) |
||||||||||||||||||||||||||||||||
|
Remarques :
Pour clarifier le dessin, il est souhaitable d’utiliser
des couleurs différentes pour chaque
année. |
||||||||||||||||||||||||||||||||
|
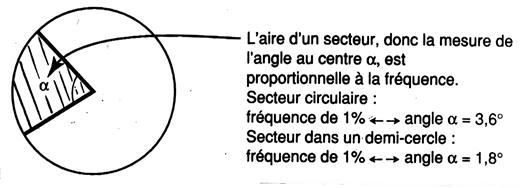
b) Le
graphique à secteurs.
( voir info +) |
|
|||||||||||||||||||||||||||||||
|
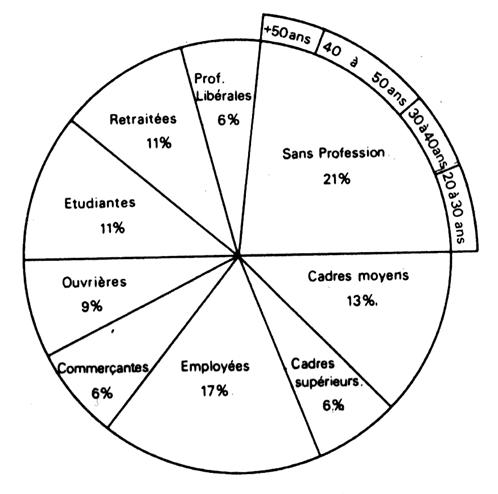
Le graphique est utilisé pour représenter les
séries statistiques non chronologiques . Ce graphique représente les
fréquences exprimées en valeurs relatives proportionnelles aux aires des
secteurs correspondants. Exemple : le graphique permet une étude de
la clientèle d’un magasin de décoration selon la catégorie socio-
professionnelle des clients. |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Remarques : Des combinaisons de cercles
concentriques permettent de représenter éventuellement des sous -
répartitions , comme vous pouvez le voir pour le secteur « sans
profession ». |
|
||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
Pour parler de l’échelle non arithmétique il faut
expliquer quelles sont les limites de l’échelle arithmétique. Sur une échelle arithmétique, des longueurs
égales représentent des accroissements égaux. Si pour un accroissement de 0 à
5 , la longueur choisie est Cette échelle dont la mise en œuvre est simple
présente cependant certains inconvénients : -
elle entraîne une
saturation rapide des graphiques dans la mesure où , par exemple, il est
difficile de représenter sur un même graphique un phénomène qui varie de 10 à
15 000 ; -
Elle induit un effet
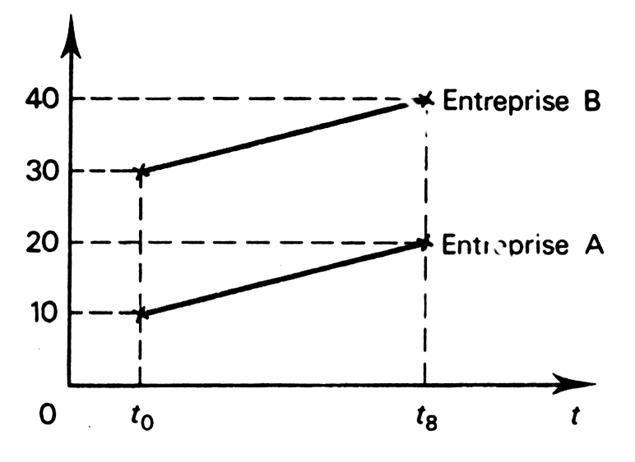
subjectif trompeur pour apprécier une croissante. Exemple : soit le
graphique, en échelle arithmétique, représentatif de l’évolution du chiffre
d’affaires de deux entreprises A et B . En ordonnée : on lit le chiffre d’affaires
en million d’euros. |
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Une lecture rapide du graphique semble indiquer
que la croissance de deux firmes a été identique : il n’en est
rien : -
la croissance de
l’entreprise A est de -
la croissance de
l’entreprise B est de Pour palier à ces inconvénients, l’utilisation
d’autres échelles est parfois préférable ou souhaitable. Ces
échelles sont soit
« logarithmique » ou « semi- logarithmique » |
|
||||||||||||||||||||||||||||||
|
|
Graphique à échelle logarithmique : a)
échelle
logarithmique. Une
échelle logarithmique est une échelle graduée proportionnellement aux logarithmes décimaux ( où
logarithmes de base 10) des nombres représentés. C’est à dire que dans cette échelle les
puissances nécessaires de 10 sont représentées par des segments
proportionnels aux exposants : Exemple : |
|
||||||||||||||||||||||||||||||
|
|
101 |
10² |
103 |
10n |
|
|||||||||||||||||||||||||||
|
1 |
2 |
3 |
n |
|||||||||||||||||||||||||||||
|
|
La distance comprise entre deux puissances
successives est appelée « module ». L’échelle logarithmique met en relief la
variation des rapports et peut - être
adoptée sur un axe du graphe. ( graphique semi logarithmique) ou sur les deux
(graphique logarithmique) |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
Nous présentons
dans ce document que le cas du graphique semi logarithmique. Ces graphiques utilisent , sur un axe , une
échelle arithmétique , et sur l’autre, une échelle logarithmique. En
général : -
l’ échelle
arithmétique est placée sur l’axe des abscisses. -
L’échelle
logarithmique est placée sur l’axe des ordonnées. Caractéristiques : 1)
ces graphiques sont
adaptés à la représentation de phénomènes qui subissent des « variations
importantes ». 2) Ils mettent en relief les phénomènes qui ont des variations relatives
constantes. La courbe représentative est alors une droite. 3) En utilisant les propriétés des logarithmes , on peut sur ces
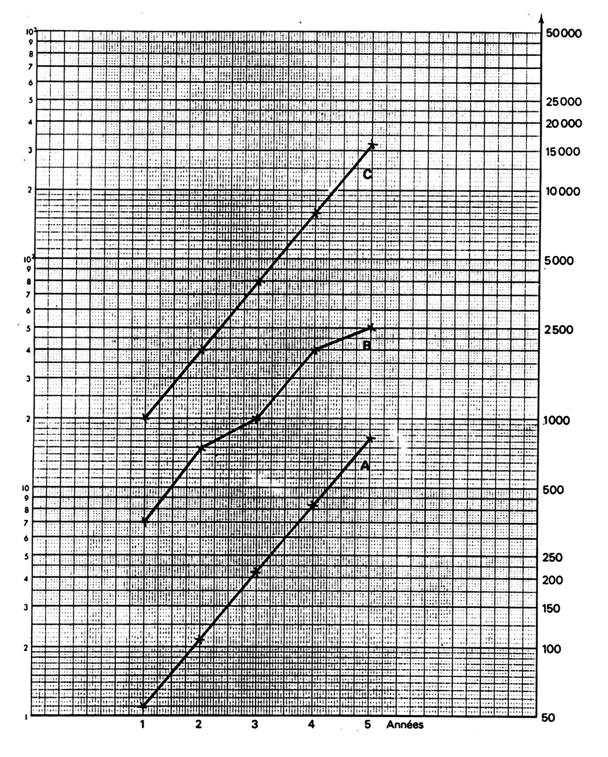
graphiques obtenir rapidement le taux de croissance du phénomène. Exemple de représentation : évolution du
chiffre d’affaires de trois sociétés A ; B ; C ( en milliers d’euros) |
|
||||||||||||||||||||||||||||||
|
|
Années |
A |
B |
C |
|
|||||||||||||||||||||||||||
|
1 |
55 |
350 |
1 000 |
|||||||||||||||||||||||||||||
|
2 |
110 |
750 |
2 000 |
|||||||||||||||||||||||||||||
|
3 |
220 |
1 000 |
4 000 |
|||||||||||||||||||||||||||||
|
4 |
440 |
2 000 |
8 000 |
|||||||||||||||||||||||||||||
|
|
880 |
2 500 |
16 000 |
|||||||||||||||||||||||||||||
|
Voir le graphique ci dessous. |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
RESUME niv V : Les Principales représentations graphiques étudiées jusqu’au niveau V .Info
++ |
|||
|
|
|
|
|
|
|
|||
|
Type de graphique |
Utiliser pour |
Description |
|
|
Diagramme « bâtons » |
Série statistique discrète |
|
|
|
Histogramme |
Série statistique dont les valeurs sont regroupées en
classes |
|
|
|
Diagramme à secteur circulaire. |
Caractère qualitatif. |
|
|
1° ) Combien y a-t-il de types de représentation
graphique de données statistiques ?
2° ) Citez deux noms de graphiques cartésiens.
3°) Citez les deux principaux groupes de
graphiques en surface :
4°) Deux types de représentations graphiques peuvent
se confondre , nommer les .
EVALUATION
corrigé CONTROLE :
1° )Combien y a-t-il de types de représentation
graphique de données statistiques ?
2° )Citez deux noms de graphiques cartésiens.
3°)Citez les deux principaux groupes de
graphiques en surface :
4°) Deux types de représentations graphiques
peuvent se confondre , nommer les .
corrigé
EVALUATION
corrigé
INTERDISCIPLINARITE