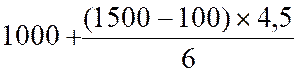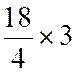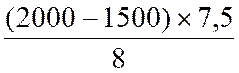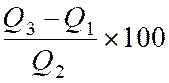Pré requis:

Les Statistiques info

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : Les indices de position.

Objectif suivant : 1°) Calculs : « étendue » ; « variance et écart type » .

tableau : l°)liste des objectifs 2°)Statistique présentation

DOSSIER : Les caractéristiques de dispersion

Les caractéristiques de dispersion sont :
	1°) L’ Etendue (rappel)  .
	2°) L’intervalle interquartile.
	3°) La variance et l’ écart type.
TEST	COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité	Corrigé Contrôle	Corrigé évaluation

	INFORMATIONS COURS
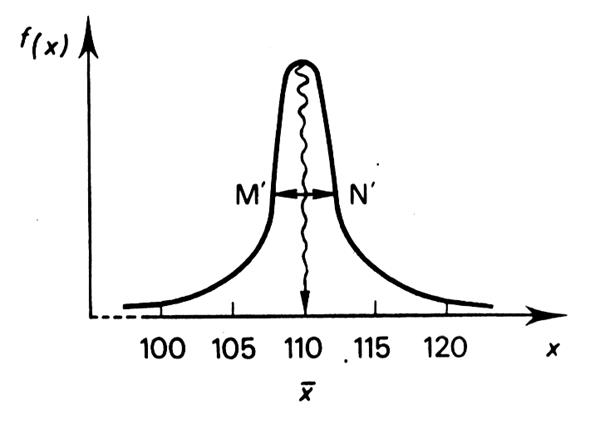
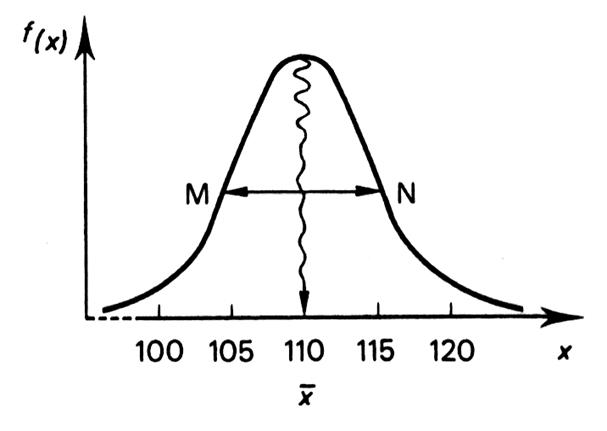
	Il arrive souvent que deux séries statistiques, bien qu’ayant des caractéristiques de position ( ou de tendance centrale) identiques , pouvaient être fort différentes.
	Exemples :
	Il faut donc , pour différencier statistiquement ces deux séries , de définir des caractéristiques de dispersion qui seront destinées à :
	- mettre en relief l’écart existant entre deux valeurs ( étendue ,intervalle interquartile) ou entre les valeurs du caractère et une valeur caractéristique centrale ( écart absolu moyen , écart type ) et - synthétiser la plus ou moins grande homogénéité des valeurs observées ( sur l’exemple MN différent de M’N’
	Important : alors que les caractéristiques de position sont des valeurs de la série statistique représentant des « points » sur l’axe des abscisses ( par exemple : = 110 ) les caractéristiques de dispersion sont des valeurs qui ne figurent pas dans la série statistique et qui représentent des segments sur l’axe des abscisses.
1°) L’ Etendue :
	La première caractéristique de dispersion est « l’étendue » Ce paramètre est également appelé « intervalle de variation ». Cette caractéristique est la plus simple mais aussi la moins significative .
	Par définition : l ‘ « étendue » ( e ) d’une série statistique est la différence entre la plus grand valeur et la plus petite valeur du caractère. Calcul : si x M est la plus grande valeur et x m la plus petite valeur alors on calculera :
			e = x M - x m
	Exemple :soit la série statistique suivante :
		x i		Fréquences ( f i )
		100		2
		105		15
		110		29
		115		16
		120		3
				65
	L’étendue est de 120 - 100 = 20
	Commentaires :Ce calcul est simple mais la simplicité de ce calcul ne doit pas nous faire oublier que « l’ étendue » est très sensible aux fluctuations des valeurs « extrêmes » qui sont souvent peu représentatives. Cette valeur caractéristique, qui correspond à un concept fort utilisé dans la pratique ( écart entre le premier et le dernier coureur , écart entre la meilleur et la plus faible note, etc.) est insuffisante pour une étude sérieuse de la dispersion.

2°) L’intervalle interquartile.						· cours sur « les quartiles ».
	1°) Définition.
	L’intervalle interquartile d’une série statistique est égal à la différence
					Q 3 - Q 1
	2°) Calcul.
	a) Arithmétique
		Exemple : xi		Effectifs.
				( n i )			Cumulés croissants
		1 000 – 1 500		6			6
		1 500 – 2 000		8			14
		2 000 – 2 500		3			17
		2 500- 3 000		1			18
				18
	Calcul préalable de Q 1 et Q 3
	1°) Calcul de la valeur de Q 1
	a) Rang de Q 1 = = 4 , 5 rang compris dans la classe 1 000 – 1 500
	b) Valeur de Q 1 =
	Q 1 = 1 000 + 375
	Q 1 = 1 375
	2°) Calcul de la valeur de Q 3
	a ) Rang de Q 3 = = 13,5 ^ème rang compris dans la classe de « 1 500-2 000 »
	b) Valeur de Q 3 = 1 500 +
	Q 3 =1 500 + 468 ,75
	Q 3 = 1 968,75
	3°) Valeur de l’intervalle interquartile.
			Q 3 - Q 1 = 1 968 , 75 – 1 375
			Q 3 - Q 1 = 593,75
	b) graphique
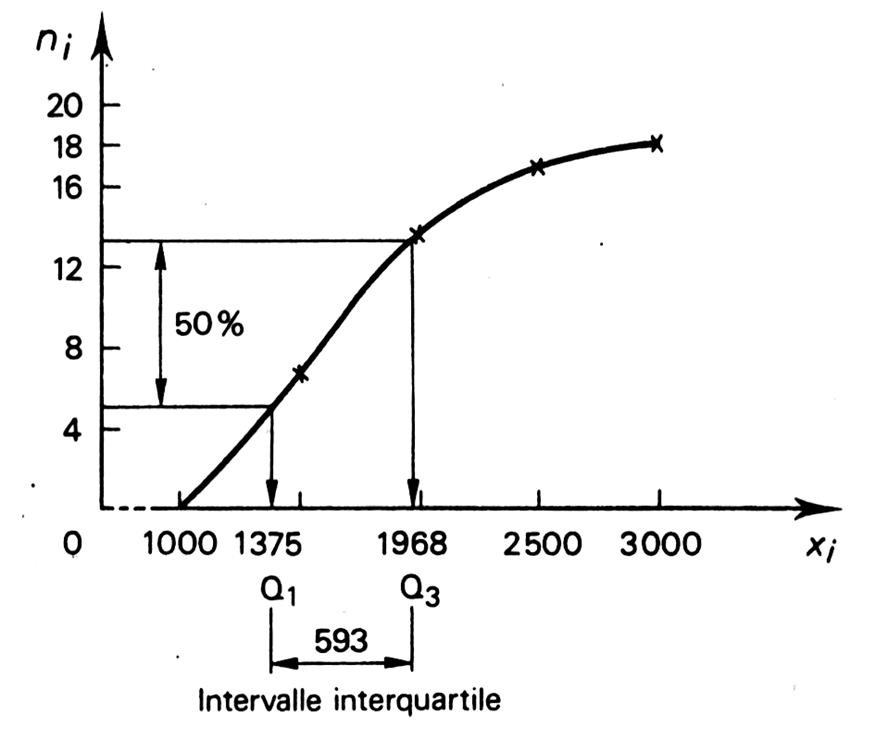
	Courbe des effectifs cumulés.
	3°) Remarques -analyses
	· Dans l’intervalle Q 3 - Q 1 = , on trouve 50 % des observations centrées autour de la médiane. Plus l’intervalle est réduit , plus la concentration autour des valeurs centrales est forte.
	· Pour la comparaison de séries statistiques mesurées en unités différentes, il est conseillé de comparer les différents « écarts interquartiles relatifs », selon la formule :

3°) La variance et l’ écart type.
	· Ici le : Cours ;…

Travaux auto-formatifs.

CONTROLE :

1° )Combien y a-t-il de types de représentation graphique de données statistiques ?

EVALUATION

INTERDISCIPLINARITE

corrigé CONTROLE :

1° )Combien y a-t-il de types de représentation graphique de données statistiques ?

2° )Citez deux noms de graphiques cartésiens.

3°)Citez les deux principaux groupes de graphiques en surface :

4°) Deux types de représentations graphiques peuvent se confondre , nommer les .

corrigé EVALUATION

corrigé INTERDISCIPLINARITE

Généralités :