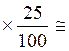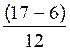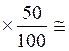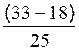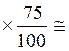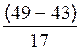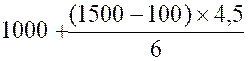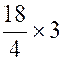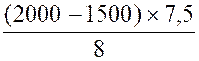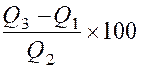Les quartiles et l'intervalle interquartile.

Pré requis :
Les Statistiques info
La fonction linéaire
Les pourcentages
Calcul numérique : le coefficient multiplicateur.
ENVIRONNEMENT du dossier:
Index : warmaths		Objectif précédent 1°) les enquêtes et observations. 2°) Voir cours niveau 5 : les « effectifs cumulés croissants »			Objectif suivant : 1°) Les moyennes. 2°) les caractéristiques de dispersion.		tableau 2°) liste des objectifs et 1°) les caractéristiques de tendance centrale et de position.

DOSSIER STATISTIQUES : les caractères de position .
les Quartiles : Mais aussi les « déciles » et les « centiles »
	1°) Définition.
	2°) détermination des « Q » : Calculs ou par le graphique.
	3°) Intérêts.
Le caractère de dispersion : L’intervalle interquartile :
	1°) Définition
	2°) Calcul
	3°) remarques et analyses.



TEST	COURS		Devoir Contrôle	Devoir évaluation		Interdisciplinarité		Corrigé Contrôle	Corrigé évaluation

CO URS

les Quartiles :

1°) définition :

on appelle « les quartiles » les 3 valeurs de la variable qui partagent l’effectif , rangé par ordre croissant , en quatre sous ensemble égaux.

Les 3 quartiles sont identifiés par les lettres abrégées : Q ₁ ; Q₂ ; Q ₃.

Par définition ,

Q₂ est l’expression de la médiane .

Q₁ est la valeur de la variable :

- Telle que l’effectif des valeurs qui lui sont inférieures représente au plus 25 % de l’effectif total ;

- Telle que l’effectif des valeurs qui lui sont supérieures représente au plus 75% de l’effectif total .

Q₃ est la valeur de la variable :

- Telle que l’effectif des valeurs qui lui sont inférieures représente au plus 75 % de l’effectif total ;

- Telle que l’effectif des valeurs qui lui sont supérieures représente au plus 25% de l’effectif total .

Exemple : les « Quartiles : Q ₁ ; Q₂ ; Q ₃ »

q1q2q3

2°) Calcul

a) Détermination arithmétique.

Calculs de Q₁; Q₂ et Q₃ ( détermination du rang et de sa valeur )

Pour le rang de « Q » on utilise le pourcentage ; pour la valeur « Q » on effectuera une interpolation linéaire.

Exemple :

x_i

Effectifs ( n_i )

simples

ECC

ECD

]1000 - 1500]

]1500 - 2000]

]2000 - 2500]

]2500 - 3000]

]3000 - 3500]

total

1°) Calculs concernant : Q₁ ( 25% des effectifs)

- Rang de Q₁ = 65 17^ème ;

- valeur de Q₁ = 1500 + (1500 - 1000) = 1500 + 458 = 1958

2°) Calculs concernant : Q₂ ( 50% des effectifs)

- Rang de Q₁ = 65 33^ème ;

- valeur de Q₁ = 2000 + (2000 - 1500) = 2000 + 300 = 2 300 (voir la correspondance avec le calcul de la valeur de la médiane)

3°) Calculs concernant : Q₁ ( 75% des effectifs)

- Rang de Q₁ = 65 49^ème ;

- valeur de Q₁ = 2500 + (3000 - 2500) = 2500 + 176 = 2676

b) détermination des « Q » par le graphique :

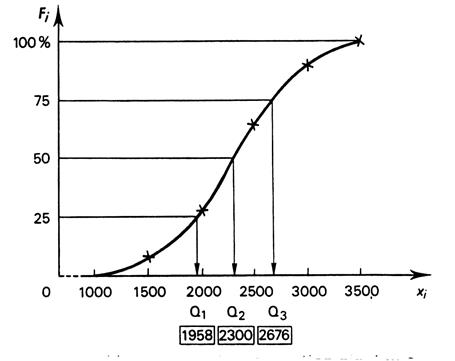
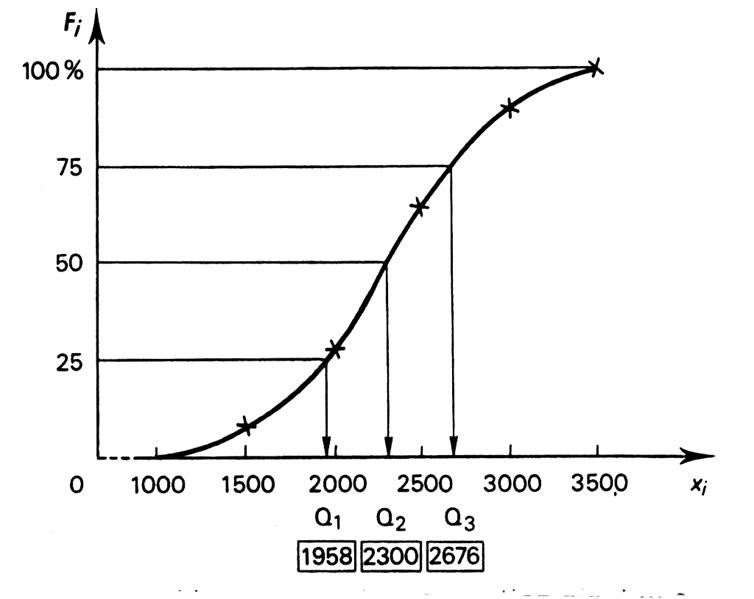
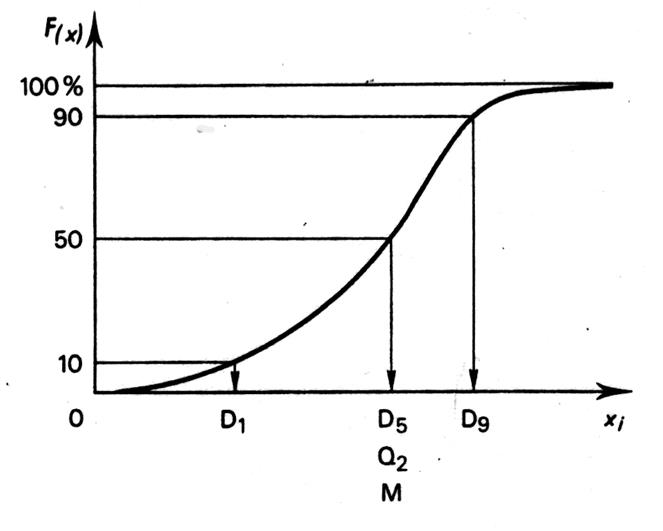
Les résultats se retrouvent graphiquement sur la fonction de répartition (vue lors de l’étude sur les ECC ; ECD , et les FCC et les FCD).

Pour déterminer les valeurs des quartiles , on repère sur l’axe des ordonnées les fréquences 0,25 , 0,5 et 0,75 , on trace des parallèles à l’axe des abscisses, puis des perpendiculaires issues des points d’intersections avec la courbe de répartition. Dans cet exemple , il apparaît que Q₁ et Q₂ sont symétriques à Q₃

Remarque : cela n’est pas toujours le cas : si la fonction de distribution n’est pas symétrique , les Q₁et Q ₂ ne seront pas symétriques par rapport à la médiane.

q1q2q3

3°) Les intérêts de connaître les quartiles .

La connaissance des Q ₁ et Q₃ est surtout intéressante pour calculer le paramètre de dispersion appelé « intervalle interquartile ».

Nous pouvons cependant déjà remarquer qu’entre les valeurs Q ₁ et Q₃ se trouve 50% de la population.

Remarque sur les « Déciles » et les « centiles » :

De la même façon ,les déciles ( D₁ à D₉ ) sont définies comme les valeurs de la variable qui partagent l’effectif rangé par ordre croissant en dix sous ensembles égaux.

Sur la courbe de répartition ci dessous , on fait figurer le premier et le dernier décile.

Enfin , les centiles ( C₁ à C₉₉ ) partagent l’effectif total en cent sous - ensembles équivalents.

Les remarques qui ont été faites sur la médiane et les quartiles s’appliquent aux déciles et aux centiles.

L’intervalle interquartile :

1°) Définition.

L’intervalle interquartile d’une série statistique est égal à la différence

Q ₃ - Q ₁

2°) Calcul.

a) Arithmétique

Exemple : x_i

Effectifs.

( n_i )

Cumulés croissants

1 000 – 1 500

1 500 – 2 000

2 000 – 2 500

2 500- 3 000

Calcul préalable de Q ₁ et Q ₃

1°) Calcul de la valeur de Q ₁

a) Rang de Q ₁ = = 4 , 5 rang compris dans la classe 1 000 – 1 500

b) Valeur de Q ₁ =

Q ₁ = 1 000 + 375

Q ₁ = 1 375

2°) Calcul de la valeur de Q ₃

a ) Rang de Q 3 = = 13,5 ^ème rang compris dans la classe de « 1 500-2 000 »

b) Valeur de Q ₃ = 1 500 +

Q ₃ =1 500 + 468 ,75

Q ₃ = 1 968,75

3°) Valeur de l’intervalle interquartile.

Q ₃ - Q ₁ = 1 968 , 75 – 1 375

Q ₃ - Q ₁ = 593,75

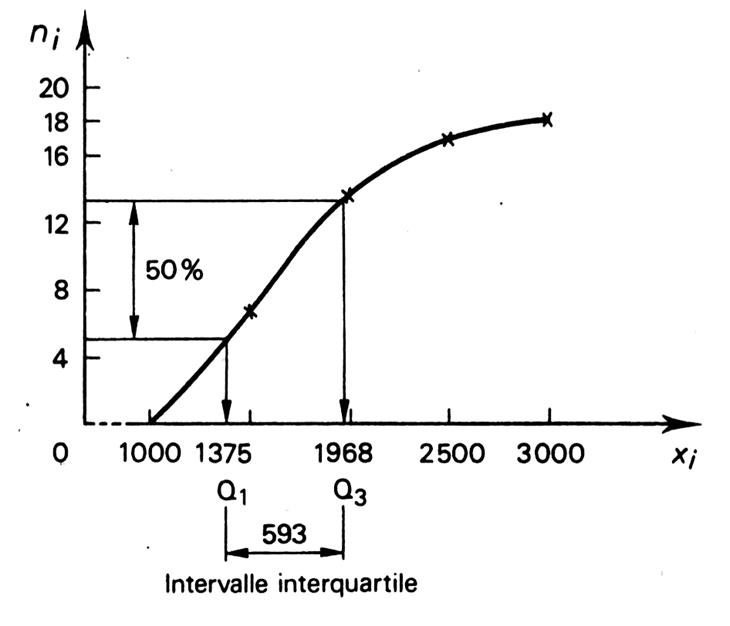
b) graphique

Courbe des effectifs cumulés.

interquartille

3°) Remarques -analyses

· Dans l’intervalle Q ₃ - Q ₁ = , on trouve 50 % des observations centrées autour de la médiane. Plus l’intervalle est réduit , plus la concentration autour des valeurs centrales est forte.

· Pour la comparaison de séries statistiques mesurées en unités différentes, il est conseillé de comparer les différents « écarts interquartiles relatifs », selon la formule :

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1°) Donner la définition des quartiles.

2°) Comment est calculer le rang et la valeur d’un quartile

3°) Comment détermine t -on la valeur du quartile dans un diagramme de répartition ?

EVALUATION

Soit le tableau ci dessous : calculer le rang et la valeur des quartiles .
x_i	Effectifs ( n_i )
x_i	simples	ECC	ECD
]1000 - 1500]	6	6	65
]1500 - 2000]	12	18	59
]2000 - 2500]	25	43	47
]2500 - 3000]	17	60	22
]3000 - 3500]	5	65	5
total	65

La correction est dans le cours.