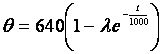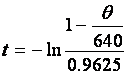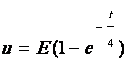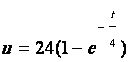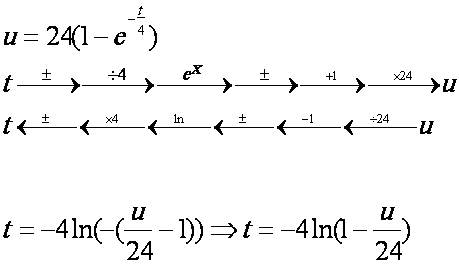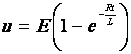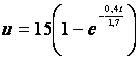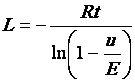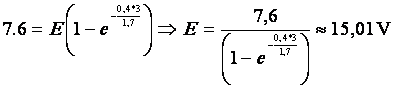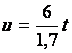Ce système a pour base le
nombre « e »b. Le logarithme népérien d’un nombre « x » s’indique par la notation log
e x ou Ln
x .
Ce système de logarithmes
népériens est particulièrement important car il intervient fréquemment en mathématiques et en physique du fait
que 
Il n’existe pas de table de
logarithmes népériens et l’on déduit le logarithme népérien d’un nombre donné
de son logarithme décimal en appliquant la règle suivante ( que l’on démontera
plus loin) .
Règle :
On obtient le logarithme népérien d’un nombre en multipliant son logarithme
décimal par « 2,30 »
Liste des cours
disponibles sur les logarithmes.
1. Exercices
préliminaires
11. Méthode
approximative pour déterminer une aire :
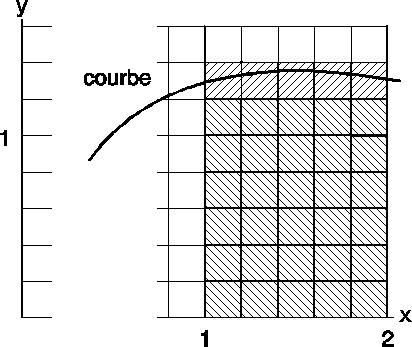
On
veut déterminer l’aire située sous la courbe délimitée par la courbe, l’axe des
x, les 2 verticales passant par x = 1 et x = 2 .
Méthode :
- on compte les carreaux entiers : 30
- on compte les carreaux coupés par la courbe : 5
- on additionne en comptant les carreaux incomplets pour moitié
total : 30 +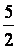 
= 32,5
- on
calcule l’aire d’un carreau :
0,2 * 0,2 = 0,04
- on calcule l’aire demandée
32,5 * 0,04 = 1,3
attention l’unité n’est bien sûr pas le
cm2 !
2. Courbe :
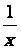
Déterminer
à partir de la courbe complète ci-dessous :
l’aire de 1 à
2 :
l’aire de 1 à 2,7 :
l’aire de 1 à 0,8 :
Le logarithme
népérien d’un nombre (noté : ln)
est donné par la mesure de l’aire située sous la courbe représentative
de la fonction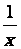 
et délimitée par les 2
droites verticales passant par le point (1 ; 0 ) et le point ( x ; 0)
Cette fonction se note : ln
si x > 1, le logarithme est positif ; si x < 1 le logarithme est négatif
Cette définition
n’est pas à savoir en bac pro.
D’après les calculs d’aires, on obtient ln(1,5) = 0,4
Compléter : ln(2) = ................... ln(2,7) = ...................
ln(0,8) = ...................
Peut-on calculer ln(x) si x < o ? ...................Peut-on
calculer ln(x) si x = o ? ...................
La fonction
ln n’existe que si x est
..............
Compléter (calculatrice) :
ln(5) = ................... ;
ln(0,08) = ................... ; ln(.............) = 0,45 ; ln(.............) = -2
4.
Base de la fonction ln
Graphiquement on a trouvé ln(2,7) » 1
Déterminer à la calculatrice le nombre qui a pour logarithme népérien 1 ln(.............) = 1
Cette valeur
est la base des logarithmes népériens et se note e
e » ......................
ln(e) = 1
Représenter graphiquement sur une feuille de papier millimétré la fonction ln
pour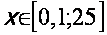 
(repère orthonormal d'unité graphique 1 cm)
6.
Propriétés de la fonction ln
61. Produit :
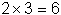
ln(2 ) = .............. ln(3) = .............. ln(6) = ..............(arrondir
tous les résultats à 10 -3)
Que remarquez vous ? ..............
Vérifier avec 5 x 2.
Compléter la formule suivante (on admettra):
62. Inverse.
remarque : a .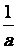 
= 1
En
utilisant la propriété du produit et la valeur de ln(1)
Compléter la formule suivante
ln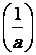 
=
63. Quotient
remarque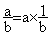 
En
utilisant les propriétés du logarithme du produit et de l’inverse
:
ln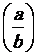 
=
64. Puissance et
racine nième:
remarque :
an = a.a.a. ………..a (n
fois)
en
utilisant la propriété du produit
Compléter la formule suivante :
ln(an)
= et on admettra : ln(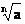 
) =
7. Exercices
71. Par tâtonnement,
trouver x tel que 2 x = 4096 réponse : ..............
On peut le trouver mathématiquement :
Si 2 nombres sont égaux, leurs logarithmes népériens sont égaux:
72. Exercices :
722. La
production d'une entreprise diminue de 6 % par an. En combien d'années
sera-t-elle divisée par 2 ?
723
Chaque année les surfaces désertiques augmentent de 1/9 de leur valeur. En
combien d’années, l’augmentation sera-t-elle de 53 % ?
LOGARITHME DECIMAL
1. Nouvelle fonction
Sur votre calculatrice, il existe une autre fonction log.
Compléter :
log(..........) = 1
La base n’est plus e mais ..........
Ce sont les logarithmes décimaux.
Cette fonction a les mêmes propriétés que la fonction ln.
2. Quel est
l’intérêt de cette fonction log ?
21. En utilisant les propriétés des
logarithmes, les puissances de 10, le fait que log(10) = 1 ; compléter en
expliquant :
sans calculatrice
log (100) = log (10 ....) = ................
log (1 000 000 ) = .........................
log (0,000 1) = ...............................
22. Toujours sans calculatrice, en
expliquant :
Sachant que log(2) » 0.3
log(20) =log(2*10) = log(2) + log(10) » 0.3 + 1 » 1.3
A vous :
log(2 000 ) »
..........
log(2 000 000 ) » ..........
log(8) » ..........
log(0.2 ) » ..........
Le
gain en puissance d’un amplificateur ou d’un filtre est donné par la
formule :
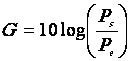
Le
gain G en décibel (dB) ; la puissance d’entrée Pe en W ;
la puissance de sortie Ps en W.
Calculer
le gain si Ps = 3 Pe G » ...................
Calculer le gain si Ps = Pe
/ 10 G » ...................
Pour un amplificateur, le gain est ..........................
Pour un filtre, le gain est ........................................
Exercices logarithmes
exponentielles
Calculs :
1. 
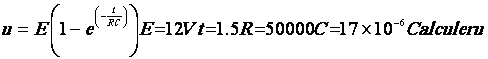
2. 
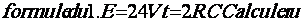
3. 
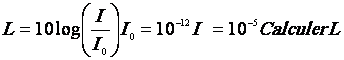
4. 
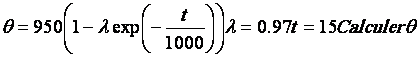
5. sans calculatrice et en
expliquant : 
Equations :
6. 
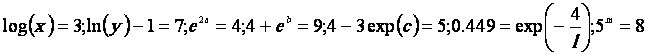
7. 
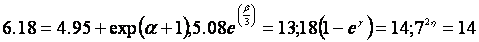
Transformation de formules
:
8. 
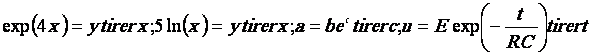
9. 
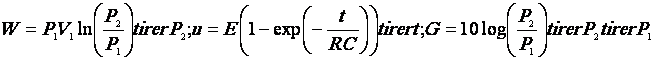
Tracés :
10. Tracer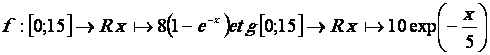 
sur la même
feuille déterminer les équations des
tangentes aux deux courbes aux points d’abscisse 0. Les tracer.
11. Tracer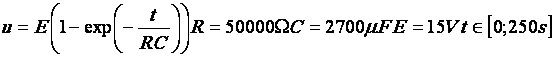 
; déterminer l’équation de la tangente au
temps t =0. La tracer.
Enoncé de bac pro msma
(extrait) :
La
température q
de la plaque à l’instant t est donnée par la relation :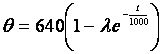 
t en secondes q en °C.
1. Déterminer l sachant qu’à l’instant t = 0 la température
de la plaque est de 24 °C.
2. On pose l
= 0.9625.
21. Montrer que t s’exprime en fonction de q par la relation :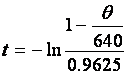 
22. Calculer le temps nécessaire pour porter la température de la plaque de 24
°C à 400°C.
3. T étant un nombre réel appartenant à l’intervalle [ -5 ; 0 ], on
considère la fonction q définie par :
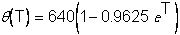
31.
Calculer la dérivée q’(T).
32. En déduire le sens de variation de la fonction q.
33. Représenter graphiquement la fonction q. Echelle : en
abscisse 2 cm pour l’unité ; en ordonnée 1 cm pour 50 unités.
Contrôle
Un condensateur est un dipôle permettant d’emmagasiner une quantité
d’électricité. Pour le charger, il suffit de le connecter à une source de
courant continu pendant un certain temps .
Soit u la tension (en volts) mesurée aux bornes du condensateur pendant la
charge. Cette tension est fonction du temps t (en secondes). Soit E la tension
(en volts) mesurée aux bornes de la source. Cette tension est constante.
u s’exprime en fonction de E et t par la relation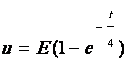 
1. Calculer E si pour t = 3 s, u = 12,7 V (arrondir le résultat à 0,1 V près)
2. Pour toute la suite du contrôle, prendre
.
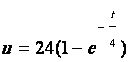Compléter le tableau de valeurs suivant (arrondir à 0,1 V près)
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
|
u
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
Tracer sur papier millimétré la représentation graphique de la fonction u(t)
pour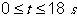 
4. Déterminer graphiquement le temps correspondant à u = 20 V.
5. Déterminer par le calcul le temps correspondant à u = 20 V
6.
Exprimer t en fonction de u.
Contrôle
Un condensateur est un dipôle permettant d’emmagasiner une quantité
d’électricité. Pour le charger, il suffit de le connecter à une source de courant
continu pendant un certain temps .
Soit u la tension (en volts) mesurée aux bornes du condensateur pendant la
charge. Cette tension est fonction du temps t (en secondes). Soit E la tension
(en volts) mesurée aux bornes de la source. Cette tension est constante.
u s’exprime en fonction de E et t par la relation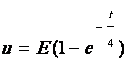
1. Calculer E si pour t = 3 s, u = 12,7 V (arrondir le résultat à 0,1 V près)
2. Pour toute la suite du contrôle, prendre
.
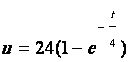Compléter le tableau de valeurs suivant (arrondir à 0,1 V près)
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
|
u
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
Tracer sur papier millimétré la représentation graphique de la fonction u(t)
pour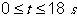
4. Déterminer graphiquement le temps correspondant à u = 20 V.
5. Déterminer par le calcul le temps correspondant à u = 20 V
6.
Exprimer t en fonction de u.
Corrigé du Contrôle
1. 
4. je lis 7,2 s
5. 
6. 
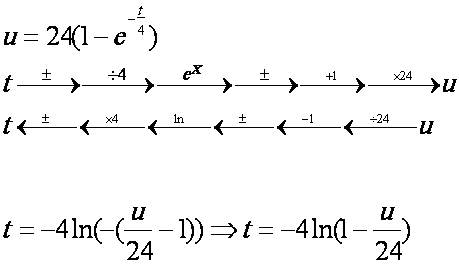
2.
|
t
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
10
|
12
|
14
|
16
|
18
|
|
u
|
0.0
|
5.3
|
9.4
|
12.7
|
15.2
|
17.1
|
18.6
|
20.8
|
22.0
|
22.8
|
23.3
|
23.6
|
23.7
|
Contrôle BPMSMA :
La tension
aux bornes d’une bobine est donnée par la formule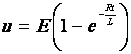 
.
E est la tension de la source, L est l’inductance de la bobine en Henry (H), R
est la résistance en W, t le temps en secondes.
1. Calculer E si u = 7.6 V quand R =
0.4 W,
L = 1.7 H, t = 3 s. (arrondir à 10-2 V)
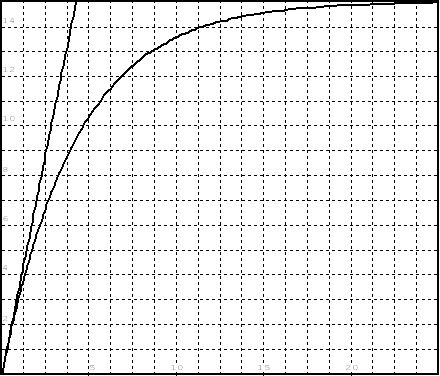
2. Tracer la représentation
graphique de la fonction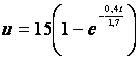 
pour t variant
de 0 à 25 s.
3. Déterminer graphiquement le temps
correspondant à u = 13 V.
4. Calculer le temps correspondant à
u = 13 V.
5. Déterminer l’équation de la
tangente à la courbe au temps t = 0. Tracer cette tangente.
6. Montrer que L s’exprime par la
formule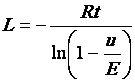 
Corrigé du contrôle :
1. 
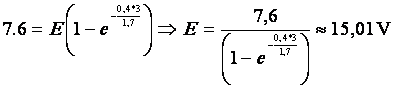
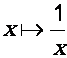
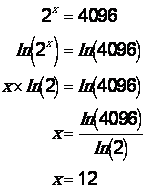
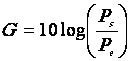
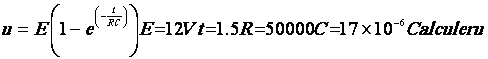
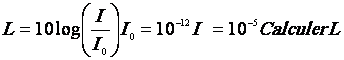
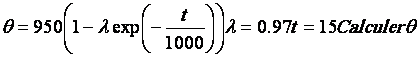
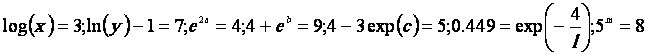
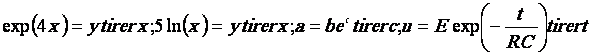
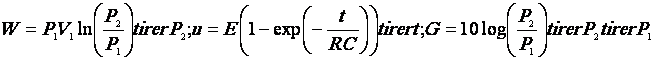
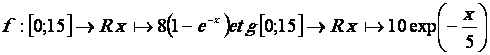
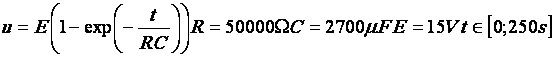