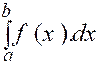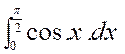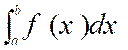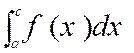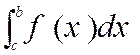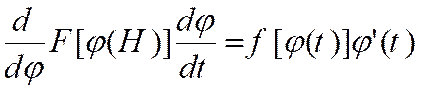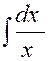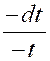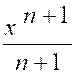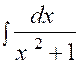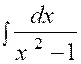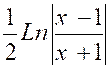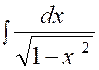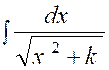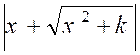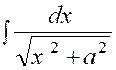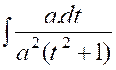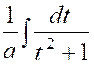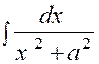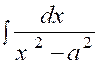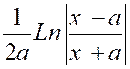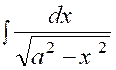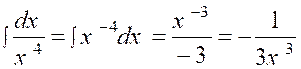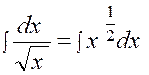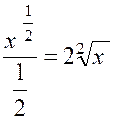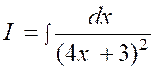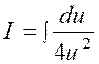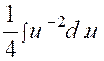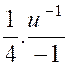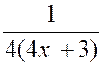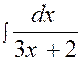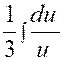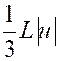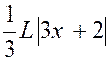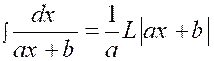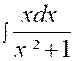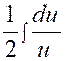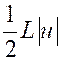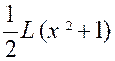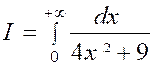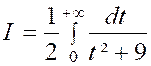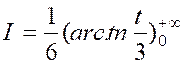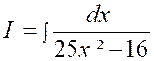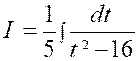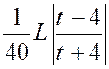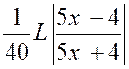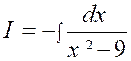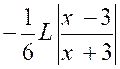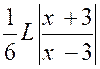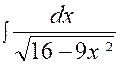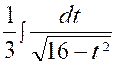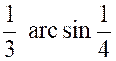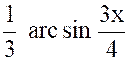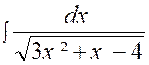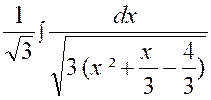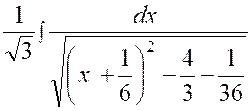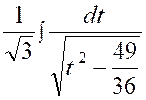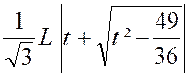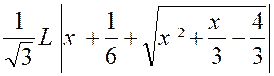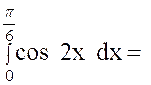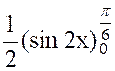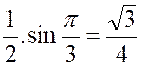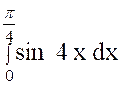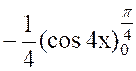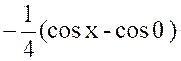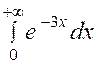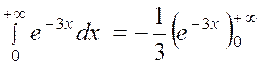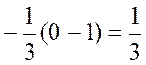1 - Primitive d’une fonction. Notation : « F (x) »

2 - Représentation graphique de la primitive par l’aire délimitée par une courbe.

3 - Intégrale définie.

4 - Explication de l’emploi du signe :

5 . Intégrale indéfinie.

6 - Changement de variable.

7- Intégrales usuelles

8- Quelques exemples simples :

COURS

1- Primitive d’une fonction. Notation : « F (x) »

On appelle « fonction primitive » ( notée : « F (x) » )ou plus simplement « primitive » d’une fonction donnée  «  f ( x) » , toute fonction « F (x) » admettant  «  f ( x) » pour dérivée.

Exemple : soit «  f ( x) = x ² » ; la fonction  « F ( x ) = »  est une primitive de  «  f ( x) ».

Plus généralement , si « C » est une constante quelconque ;  « F ( x ) =  + C » est aussi une primitive de «  f ( x) = x ² »

Il en est ainsi dans tous les cas : on obtient toujours une primitive d’une fonction donnée en ajoutant une constante «  C » arbitraire  à une primitive particulière.

2- Représentation graphique de la primitive par l’aire délimitée par une courbe.

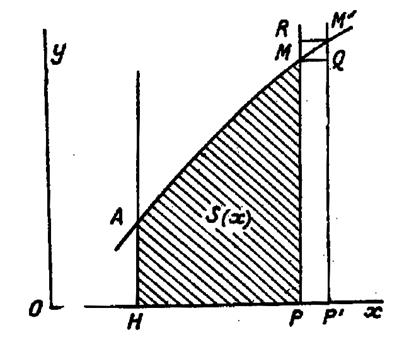
Traçons la courbe représentative des variations de la fonction «  f ( x) ».et pour fixer les idées, supposons la fonction positive et croissante ( voir ci contre).

Ensuite considérons la surface limitée par l » axe « Ox », une ordonnée (c'est-à-dire une parallèle à « Oy »)fixe « AH » et une ordonnée variable « MP ».

Cette surface « S » est fonction de l’abscisse « x » du point « M »

Nous allons voir que « S » est une primitive de «  f ( x) ».

En effet , donnons à « x » un accroissement « PP’ =  x  »

L’aire  « S »   prend un accroissement  « S  » , soit l’aire limitée par  « PP’  M M’ »

Par « M M’ » , menons des parallèles à « Ox ». Nous formons  ainsi deux rectangles  « PP ’ QM » et  «  P P ‘ M’R » entre lesquels est compris « S  ». On peut donc écrire :

«  y.  x   <   S  <   x ( y +   y ) »    

Quand «  x » tend vers zéro, il en est de même de «  y »

Par suite  «  » tend vers la dérivée  «  »  de « S »  par rapport à « x ».

Il est donc bien démontré que « S » admet « y » pour dérivée ; ou ce qui revient au même :

L’aire d’une courbe peut être considérée comme une primitive de la fonction «  f ( x) ».

Remarque :

Le raisonnement précédent fait comprendre pourquoi une fonction donnée admet une infinité de primitives différant entre elles par une constante arbitraire.

                       En effet , l’aire « S ( x )» peut être évaluée à partir d’une ordonnée origine « AH »quelconque. Modifier « AH » revient à ajouter ou retrancher une constante à l’aire « S ( x )»

3 - Intégrale définie.

            Cherchons à évaluer l’aire « a A B b » (voir ci contre)   limitée par la courbe « y = f ( x ) » , l’axe « O x » et les ordonnées des points « A » et « B ».

Nous pouvons la considérer comme la différence entre les aires «  H K B b »  et « H K A a ».

Soit d’autre part , « S ( x ) une primitive de « f ( x ) » elle peut être représentée par l’aire «  H K M P »évaluée à partir de l’ordonnée fixe «  H K »

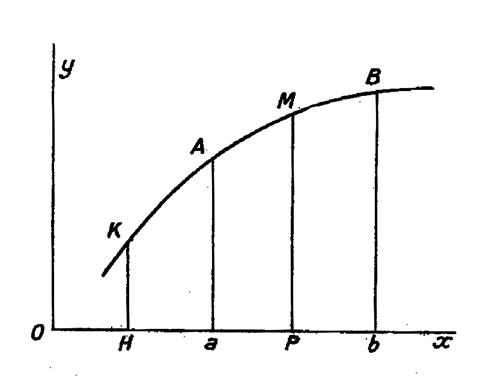
L’aire « a A B b » est donc  la différence entre les deux valeurs extrêmes de la primitive , soit : «  S (b)  - S (a) »

Cette aire s’appelle une intégrale définie. ON la représente par la notation :

qui  s’énonce : Somme de « a » à « b » , de « f ( x ) dx »

On peut donc écrire    =  S ( b ) – S ( a )

Exemple

Soit l’intégrale définie :;

La fonction «  f ( x ) = cos x »    admet pour primitive « F ( x ) = sin x » , puisque « cos x »est la dérivée de « sin x ».

On a donc :

  =    =    sin  - sin 0  = 1

Remarque :

Permuter les limites d’intégration revient à changer le signe de l’intégrale. En effet , on a :

=  S ( b ) – S ( a )      et          =  S ( a ) – S ( b )

et par suite :

=  -

Dans un même ordre d’idées , on a aussi :

  =       +    

En effet , cela revient à dire que :  S ( b ) – S ( a )   =   S ( c ) – S ( a ) + S ( b ) – S ( c )

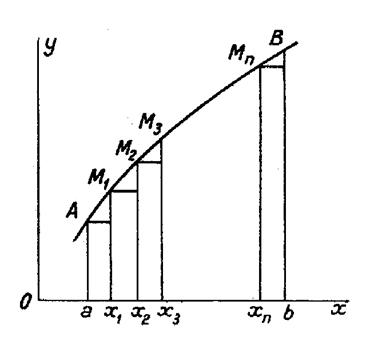
4 - Explication de l’emploi du signe :

Pour évaluer l’aire « a A B b » on peut procéder ainsi :

Partageons l’intervalle  « ( a , b ) » à l’aide de valeurs intermédiaires :  « x₁ » ; « x₂ » ; …… ; « x_n ».

Par les points « M₁ » , « M₂ », …………….« M_n » correspondants menons des parallèles  à l’axe « O y ».

Nous décomposons ainsi l’aire en trapèzes curvilignes dont  il s’agit de calculer la somme.

Chacun de ces trapèzes diffère peu du rectangle inscrit. Par suite , une valeur approchée de l’aire  « a A B b » est :

« ( x₁ – a )  f ( a ) +    ( x₁  -  x₂ ) f (x₁  ) +    ………..+   ( b - x_n ) f (x_n ) »

ou  encore :                  

Le signe  «  » signifiant qu’il faut faire la somme de tous les termes analogues lorsque « k » prend toutes les valeurs possibles de « 1 » à « n ».

Il est logique d’appeler «  x _k » l’accroissement «  x _k+1 -  x _k » pris par « x » quand on passe d’une valeur de « x » à la valeur suivante.

On peut dons écrire la somme des aires des rectangles sous la forme :

Supposons maintenant que le nombre des rectangles inscrits augmente indéfiniment , chacun d’eux tendant vers zéro.

La somme précédente a pour limite l’intégrale définie. Les accroissements  «  x » peuvent être assimilés à des différentielles «  dx » et :

  tend vers

le signe  «   » est la déformation de la « S » et aussi cette forme ancienne de cette lettre , rappelle qu’une intégrale est une somme d’un nombre infiniment grand d’infiniment petits.

5 . Intégrale indéfinie.

Une intégrale indéfinie est de la forme «  »

Elle ne contient pas de limites d’intégration et elle représente , par définition, une primitive quelconque de la fonction «  f ( x ) »

Autrement dit, une intégrale indéfinie n’est calculable qu’ à une constante prés.

Exemple :  =  C + sin x »

6 - Changement de variable.

Soit l’intégrale indéfinie : I  =

Substituons à « x » une autre variable « t », à l’aide d’une relation de la forme «  x = ( t ) » et  « d x » par «   ‘( t ) d t ». Autrement dit :  «  I =   »

En effet , soit « F ( x ) » une primitive de «  f ( x) ».

Il en résulte que : «  » =   « F ( x ) »

Avec :  «  F ( x ) =  f ( x) ».

Quand on remplace « x » par «  ( t ) » , « F ( x ) » devient une fonction de « t » par l’intermédiaire de « x ».

L’intégrale prend la forme : I  =  et tout revient à trouver «  H ( t ) »

Or , on a :   =  F [( t ) ]

Et :

Par définition d’une intégrale , cela entraîne que «  H ( t ) » est la dérivée du second membre par rapport à « t ».

C’est une dérivée de fonction de fonction. Par suite : «  H ( t ) =      »

Remarque :

Dans  le cas d’une intégrale définie , il faut chercher les nouvelles limites d’intégration pour la nouvelle variable.

Exemple : soit l’intégrale   « I = ( 3 x + 4 ) ⁵ dx . »

Posons :  « 3 x + 4 = t »  d’où «  3 dx = dt »

                                                                  D’autre part :

-        Pour « x = 0 » , «  t = 4 »  et  pour  «  x = 1 »  , «  t = 7 »

Par suite :

« I = ( t ) ⁵ d t . » =   ( t  ⁶)  = 

7- Intégrales usuelles

Puisque la relation  «   » = g ( x ) + C  équivaut , par définition :   «  [  g ( x ) ]  =  f ( x) ».

Il en résulte qu’en lisant à l’envers un tableau de dérivées, on peut ainsi former un premier tableau d’intégrales usuelles .

Exemple : la dérivée du (logarithme népérien)  est : «   Ln  ( x )   =  ».   Par suite : =  Ln x

Nous sous entendrons , chaque fois, la constante d’intégration pour simplifier l’écriture.

Remarquons que la fonction «  Ln x » (logarithme népérien)   n’est définie que si « x » est positif. Supposons maintenant « x » négatif .Et posons «  x = -t »  de sorte que « t » est positif. On a alors : «  d x = - d t » et par suite :

«  =  =   = Ln ( t )  =   L n ( -x) »

Or ( -x ) n’est autre que la valeur absolue de « x » soit  «  »  . Nous écrirons donc : « =  Ln  »  quel que soit le signe de «  x »  .

En appliquant le même raisonnement aux fonctions  les plus simples , nous obtenons un tableau d’intégrales nouvelles.

  dx   =      (   n -1)

Et  si « n = -1 »

=  Ln  

   =  arc tan x

   =

   =  arc  sin x

   =  Ln

 =  sin x

 = - cos  x

d x =  

Mais dans les applications , il est préférable de changer légèrement la forme de ces intégrales usuelles. Nous allons détailler la raisonnement pour l’une d’elles ; ce serait la même chose pour les autres ;

Soit , par exemple , à calculer l’intégrale :  I  =     « a » étant constant.

Pour nous ramener à la troisième des intégrales usuelles précédentes , faisons le changement de variable.

  «  x = a . t »   d’ où «  d x = a . d t »   et  

«  I  =   =    =   arc tan t »

ou finalement :  I  =   arc tan »    ;  nous pouvons maintenant former le tableau sous sa forme définitive.

Voir les exemples à la suite

1.      

  dx   =      (   n  - 1)

(1)

2.     et si « n=-1)

=  Ln  

(2)

3.      

  =    arc tan

(3)

4.      

   =

(4)

5.      

   =  arc  sin

(5)

6.      

   =  Ln

(6)

7.      

 =  sin mx

(7)

8.      

 = - cos m x

(8)

9.      

d x =   

(9)

8- Quelques exemples simples :

(1)

Calculer :

De la forme :

  dx   =      (   n  - 1)

(1)

 = 

Calculer : 

Nous posons  « 4x + 3 » = « u » ; d’où la dérivée  « d.u = 4 dx »  et   ;   =   = 

(2)

Calculer :

De la forme

=  Ln  

Nous posons : 3 x + 2 = u   ; d’où   d.u =  3 dx , et l’intégrale devient :

=   = 

Plus généralement :  , « a » et « b » étant des constantes , on a : 

Exemple :  calculer  ; nous posons «  x² + 1 = u » , d’où : « 2x dx = du »  et l’intégrale devient :  =   =   ou encore :

(3)

Calculer :

Posons « 2x = t » , d’où : « 2 dx =dt »   et   ; en effet , les limites d’intégration pour la nouvelle « t » sont « 0 » et  « +  » . Par suite :

  =  

(4)

Premier exemple :

Calculer :

De la forme :

   =

Nous posons « 5x=t » ; d’où : 5 dx = dt », et l’intégrale devient :

 =    =

Deuxième exemple :

 ;   =

(5)

Soit : 

Posons «  3x = t » , d’ où « 3dx = dt » et l’intégrale devient :

  =   =

( 6)

Calculer : 

De la forme :

   =  Ln

 On peut écrire :

=      =  

Posons «  x + =t »   d’où « dx = dt »  et l’intégrale devient :   ou 

Soit 

( 7 )

Calculer     = 

De la forme :

  =  sin mx

  = 

( 8 )

Calculer    :     =

De la forme :

 = - cos m x

  =   =

( 9 )

Calculer :

De la forme :

d x =   

  = 

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!voir les définitions en « orange » !!!!!

EVALUATION :

Calculer : l’intégrale   « I = ( 3 x + 4 ) ⁵ dx . »

Voir le cours !!!!!

Calculer :

(1)

Calculer :

De la forme :

Calculer : 

(2)

Calculer :

Calculer  ;

(3)

Calculer :

(4)

Calculer :

Calculer :

 ; 

(5)

Calculer : 

( 6)

Calculer : 

( 7 )

Calculer     = 

( 8 )

Calculer    :     =

( 9 )

Calculer :