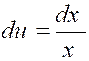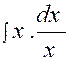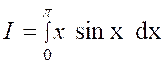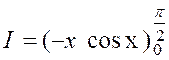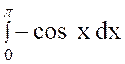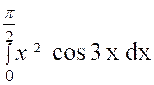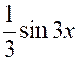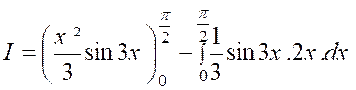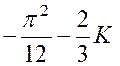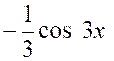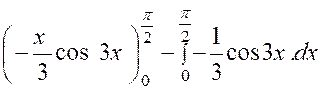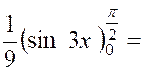COURS

Cette méthode  est assez générale, elle tire son nom du fait que l’on commence par intégrer seulement une partie de la fonction donnée :

La formule  d’intégration par parties s’écrit :

 =   u v - 

En effet , « u.v » un produit de deux fonctions de « x » .

On sait que sa dérivée  est    :

Donc , en intégrant , on a , à une constante prés :

Mais d’après la définition d’une différentielle , ( info) , on sait que :

D’ où :   

C’est précisément la formule à démontrer.

Exemple : soit à calculer

Posons «  L x = u »  et «  dx = dv »

On en déduit :    et  «  v =  = x   ( intégration d’une partie de l’intégrale)

Par suite :  = x  L x  -   =  x  L x  -   x L x – x

Remarque 1 : Pour appliquer la formule d’intégration par parties , il faut choisir convenablement « u » et « v » . On s’arrange , naturellement , pour simplifier au lieu de compliquer.

Soit l’intégrale :   

Il serait évidemment maladroit de poser «  sin x = u »  et «  x dx = dv » , car on aurait «  v =   =    e « x » figurerait au second degré , ce qui serait encore plus gênant qu’au premier.

Au contraire , en posant :

«  x = u »    et  « sin x dx = dv »,

on a   :   du = dx ;      « v = - cos x »

et :

 -   =    = 

L’intégration par partie a réussi, parce qu’elle a fait disparaître le facteur « x » en donnant une intégrale purement trigonométrique.

Remarque 2 :

Il peut se faire que  l’on ait à intégrer par parties plusieurs fois de suite.

Soit l’intégrale :

Intégrons  une première fois par parties en posant : «  x ² = u »   ; « cos 3 x dx = dv »

Nous obtenons :

«  d u = 2 x dx »    ; v =

et :   = 

Pour calculer l’intégrale « K » appliquons une seconde fois la méthode en posant : «  x = u₁ » ; « sin 3 x dx = d v₁ »

D’où : «  d x = d u₁ » ; v ₁  =

Par suite :

 «  K =    =  

D’où :   = - 0,748

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!!voir les définitions en « orange » !!!!!

EVALUATION :

Calculer :

1.     

2.     

Voir le cours !!!!!