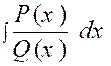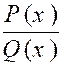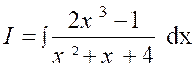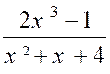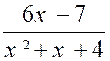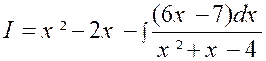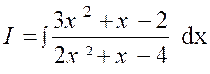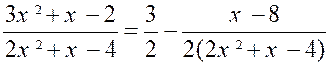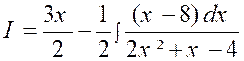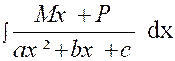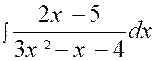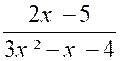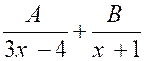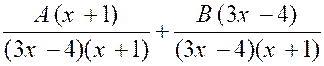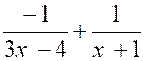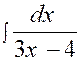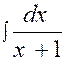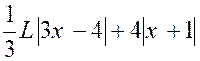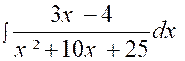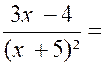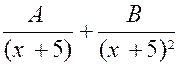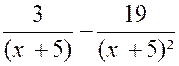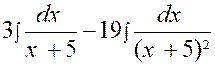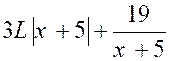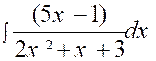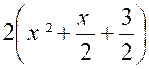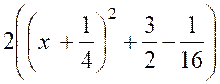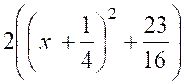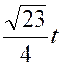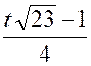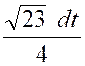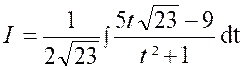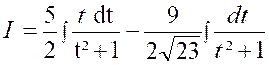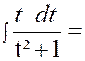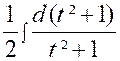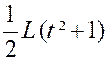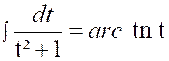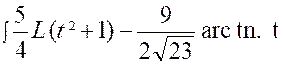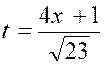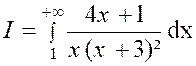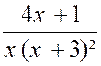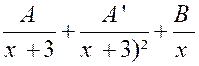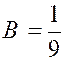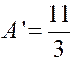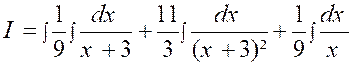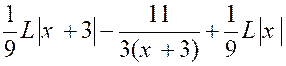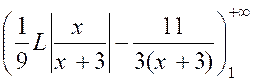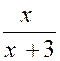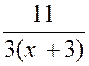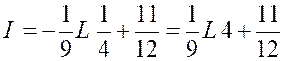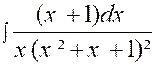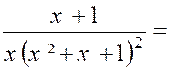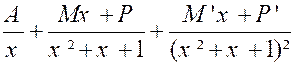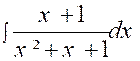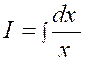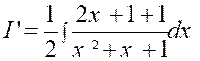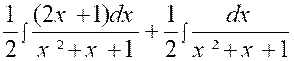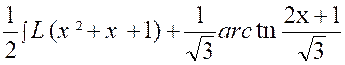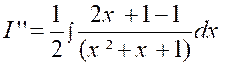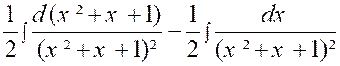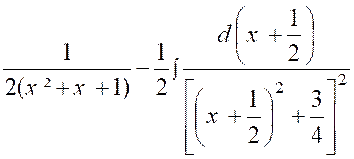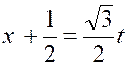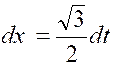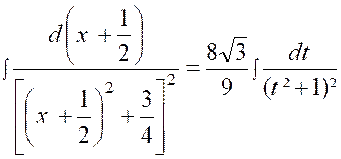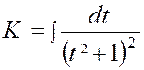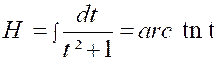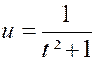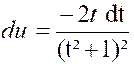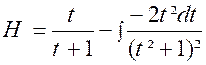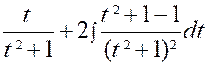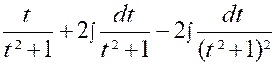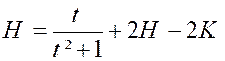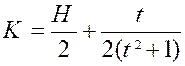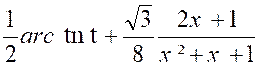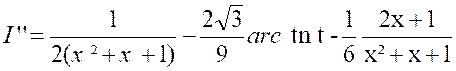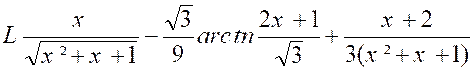COURS

On appelle  ainsi les intégrales de la forme :  ; P (x) et Q (x)  étant deux polynômes.

Nous pourrons toujours nous ramenez au cas où le degré  de «  P ( x ) » est inférieur au degré de «  Q ( x ) » ;
S’il en était autrement , on ferait la division de  «  P ( x ) » par «  Q ( x ) » par puissances décroissantes et on aurait d’abord à intégrer la partie entière de la fraction  ce qui ne présente aucune difficulté.

Exemple 1 :

Soit l’intégrale :

En divisant le numérateur par le dénominateur on obtient :

En divisant :  = 2 x – 2  - 

Et :   

Exemple 2 :

Soit l’intégrale :  

On a de même :

Et

Cela posé nous étudierons quelques cas visuels simples en exposant les méthodes sur des exemples numériques.

Soit d’abord l’intégrale :

Pré requis : savoir résoudre l’équation du second degré  : 3 x² - x – 4

1°) Si les racines du dénominateur sont réelles et distinctes , on décompose la fraction à intégrer en une somme de deux fractions plus simples.

Exemple :  ; les racines du dénominateur sont « -1 » et «  »

On peut donc écrire :  3 x² - x – 4  =  ( 3 x – 4 ) ( x + 1 )

Cherchons alors deux constantes « A » et « B » telles que : = 

 =  

Pour obtenir « A » et « B » nous chassons les dénominateurs :

On obtient :    2 x – 5 = A ( x + 1 ) + B ( 3 x – 4 )       et  nous remplaçons  successivement « x » par «  »  et par « -1 »

a)    2 x – 5 = A ( x + 1 ) + B ( 3 x – 4 ) ; on calcule :    2  – 5 = A ( + 1 ) + B ( 3  – 4 ) ;  2  – 5 = A ( + 1 ) + B ( 0 ) ; A = -1.

b)    2 x – 5 = A (x + 1 ) + B ( 3 x – 4 ) ; on calcule :    2 ( -1)  – 5 = A (( -1) + 1 ) + B ( 3 ( -1) – 4 ) ;  2 ( -1) – 5 = A (0 ) + B (+1 ) ; B = +1.

D’où :

= 

Par suite :    =  -    +   = 

2°) Si les racines du dénominateur sont égales, on décompose la fraction à intégrer de la façon suivante :

Exemple :  ;  on a  « x² +10 x + 25  =  ( x + 5 )² »

    en réduisant au même dénominateur , puis en chassant les dénominateurs  , nous obtenons :

3x – 4 = A ( x+5) + B

Ensuite on cherche les valeurs de « A » et « B » :

 A = 3  

Puis 5 A + B = -4  d’où  «  B = - 19 »

Et par suite    ;

Et    =   = 

3°)  Si les racines du dénominateur sont imaginaires, on décompose le trinôme en une somme de deux carrés et on simplifie par un changement de variable.

Exemple : soit l’intégrale :   on peut écrire :

2x² + x + 3  =  =  =

Posons «  x +  =   d’où «  x =  » et « dx   =  » de sorte que l’intégrale  devient :  

Elle se décompose en deux intégrales plus simples :

on a successivement :

 =    et   ;

D’où    avec

Cas  où le dénominateur  «  Q (x) » de la fraction à intégrer n’a que des racines réelles.

Le résultat peut contenir des logarithmes , mais certainement pas d’arcs tangentes ( arc. tn.)

Exemple : soit l’intégrale :

Décomposons d’abord la fraction à intégrer sous la forme.

 = 

Pour calculer les coefficients « A » ; « A’ » , »B », chassons les dénominateurs :

4x +1 = A ( x + 3) x + A ‘ x + B ( x + 3 ) ²

et identifions :

« 0 = A + B » ;  4 = 3 A + A’ + 6 B » ; 1 = 9B  on déduit de là :

A =    ;   ;

L’intégrale s’écrit :

  =   ; =

Pour « x =  » ,   tend vers l’unité , son logarithme tend vers zéro , et   tend aussi vers zéro.

Par suite :

Cas  où le dénominateur  «  Q (x) » de la fraction à des racines imaginaires .

Le résultat peut contenir à la fois des logarithmes et des arcs tangentes.

Exemple :

Soit l’intégrale :

Cherchons à mettre la fraction à intégrer sous la forme :

Pour calculer les cœfficients  «  A ; M ; P ;M’ ; P’ », réduisons au même dénominateur ; puis transformons l’égalité : chassons les dénominateurs.

«  x+1 = ( x² + x + 1)²  + ( M x + P ) x.  ( x² + x + 1) +  x ( M ’ x + P ‘ )  et identifions :

0 = A + M   ;  0 = 2A + M + P   ;   0 = 3A + M + P + M’   ;   1 = 2A + P + P ‘   ; 1 = A

Nous obtenons :  «  A = 1   ; M  = - 1  ; P  = - 1   ;M’  =  - 1  ; P’ = 0 »

Et l’intégrale se met sous la forme :

 =   -  - 

On a d’abord :

  = 

puis

  =   = 

Enfin :

  =   = 

Pour calculer cette dernière intégrale , posons :

«  »  d’où «   et cette intégrale devient :    

  et il ne reste plus qu’à calculer l’intégrale : 

Pour cela , nous partons de l’intégrale :  

 et nous intégrons « H » par parties en posant    et « dv = dt » ;On  a alors :     et « v = t »

De sorte que :

  =   =

ou                              On en déduit :

          =    K =  

par suite :      et la valeur de l’intégrale s’obtient en remplaçant «  »  par les expressions trouvées.

  = 

CE qui termine  ce cours…………..

TRAVAUX AUTO FORMATIFS.

CONTRÔLE

Voir le cours !!!!! voir les définitions en « orange » !!!!!

EVALUATION :

Calculer :

Voir le cours !!!!!