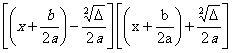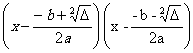résoudre et factoriser une équation du second degré (trinôme)

DOC. : Professeur ; Formateur

DOC : Formation Individualisée

DOC : Elève.

 

DOSSIER  N°      Matière : MATHEMATIQUE

Information « TRAVAUX » ;Cliquer sur  le mot !.

INFORMATIONS PEDAGOGIQUES :

Formation :       NIVEAU  IV :

OBJECTIFS :- Savoir résoudre  une équation du second degré ;       «  a x² + b x + c = 0 »  

I ) Pré requis:

1-

Cours de niveau V (repérage)   BEP - CAP

 

2-

Pré requis tracés géométriques

:i

3-

Cours niveau V sur la fonction (en BEP)

:i

4 -

TESTS : Calculs ( série E , et toute la partie 2)

:i

5-

TESTS : tracés (série 1 : n°6 et série 2 : n°5)

:i

6 -

INFO :   Représentation graphique d’une fonction

:i

II ) ENVIRONNEMENT du dossier :

Index  

Dossier précédent :

Résoudre

Dossier suivant :

  1. Résoudre une équation du second degré…….
  2. résoudre une inéquation du second degré

Info : Tableau synoptique  :i

III )  LECON  n° :    Factorisation d’un trinôme du  SECOND DEGRE

Chapitres :

 

 

 

 

 

:i

IV)   INFORMATIONS  «  formation leçon » :

 

Test

 

COURS  

Travaux  auto - formation.

 

Corrigé des travaux  auto - formation.

Contrôle

évaluation

INTERDISCIPLINARITE

Corrigé Contrôle

Corrigé

 évaluation

 

V )   DEVOIRS  ( écrits):

 Devoir diagnostique L tests.

Ÿ

 Devoir  Auto  - formatif  (intégré au cours)

Ÿ

  Devoir Formatif  « Contrôle : savoir » ;   (remédiation)

Ÿ

 Devoir  Formatif  «  Evaluation   savoir faire »  (remédiation)

Ÿ

Devoir sommatif.

Ÿ

Devoir certificatif : (remédiation)

Ÿ

* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .

 

Leçon

Titre

N°

FACTORISATION DU TRINOME du SECOND DEGRE

CHAPITRES

 

Définition

 

 

Résoudre

 

i9   

Calcul du discriminant

:i

 

COURS

 

i9  

 Définition

:i

 Une équation du second degré d’inconnue « x » est une équation de la forme :

                                                           a x² + b x + c = 0

 

« a », « b », « c » sont les coefficients ( ce sont des nombres réels) ; et   « a » "` 0

 

info :  a x² + b x + c = 0  est  un trinôme de degré deux , appelé « polynôme du second degré ».

Activité :   x² + 2 x = -1       se ramène à la forme      x²  + x   - 1 = 0

                3 x² =  + 2x - 5   se ramène à la forme    3x²   - 2 x + 5 = 0

                  x²  =  9 x  - 6  se ramène à la forme x²  - 9 x + 6 = 0

 

i9   

Résoudre  l’équation de la forme a x² + b c + c = 0

:i

 

 

a x² + b c + c = 0

 

 

 

 

 

 

 

Calcul du discriminant :

  ∆  = b² - 4 ac

 

 

 

 

 

 

si

 

si

 

si

∆  > 0

 

∆   = 0

 

∆   <  0

alors

 

Alors

 

Alors

Deux solutions :

x’ =

x’’ =

 

Une solution :

 

x’ = x’’ =

 

 

Aucune solution

Remarques :

 la première solution  se note  , invariablement ,   :     x’ (lire :  ixe prime)  ou   x1  ( lire : ixe indice 1)

la deuxième  solution  se note  , invariablement ,   :    x’’ (lire ixe seconde) ou   x2   ( lire :ixe indice 2)

 

EXEMPLES DE RESOLUTION : (parfois Il faut transformer l’égalité et ramener l’équation à la forme d’un polynôme du second degré  ( vu précédemment) )

 

 

Cas  1 :      résoudre    x²  - 9 x + 6 = 0

 

Procédure :

   x²  - 9 x + 6 = 0   ;  x’ = ?  et   x’’ = ?

Identifions  les coefficients

  a =  1  ; b = -9 ; c = 6

Calcul du discriminant ” = b² - 4 ac

(-9) ²  - 4 × 1 × 6 ;  =  81 - 24 ;  =  57

Analyse du signe et du résultat de ”

1ère conclusion :

Le discriminant est  >0 ;  positif

Le discriminant étant positif l’équation a …2…solution (s)

Calcul de la racine de ”  ( )

  #  7,55

Calcul de la ou des solutions :

 

x1  = = 8,275

 x2  =   =0,725

 

2ème conclusion :

  x²  - 9 x + 6 = 0

admet deux solutions ;

  à pour solutions (racines)       8,275 et 0,725

Activité : résoudre    7 x² + 5 x - 38 = 0            ( x’ = 2 ; x’’ = )

Cas 2 :      résoudre   25 x²  - 30 x + 9 = 0

 

Identifions  les coefficients

  a = 25   ; b = - 30 ; c = 9

Calcul du discriminant ” = b² - 4 ac

( - 30)² -  4 × 25 × 9 ;  900  -  900  =  0

Analyse du signe et du résultat de ”

1ère conclusion :

Le discriminant est  nul  (= 0)

L’équation a 2  solution (s)  égales.

 

Calcul de la racine « double »

    

 

Calcul de la ou des solutions :

x ‘ =  x ‘’  =  =   = 0,6

 

2ème conclusion :

25 x²  - 30 x + 9 = 0

a  pour solution unique    x ‘ =  x ‘’  =  0,6

 

 

 

Cas 3 :      résoudre   2 x²  - 4 x + 5 = 0

 

Identifions  les coefficients

  a = 2   ; b = - 4 ; c = 5

Calcul du discriminant ” = b² - 4 ac

( - 4)² -  4 × 2 × 5  =  16 - 40 = -30

Analyse du signe et du résultat de ”

1ère conclusion :

Le discriminant est  négatif

L’équation n’admet pas de solution

 

 

 

i9  

FACTORISATION : Démonstration  sur la factorisation du polynôme           a x² + b x + c

1°) Forme canonique :i  2°) Factoriser :

Pour factoriser il faut connaître les racines de l’équation !donc avant de factoriser il faut « résoudre ».

Application numérique

Cas général

 

Résoudre l’équation x² - 4 x + 3 = 0 

 

 

Résolution de l’équation a x² + b x + c =0 

Le coefficient  « a » ¹ 0

 

Factorisons le polynôme :

 

·        - 4 x  = - 2 × 2 × x

·        x² - 4 x  sont les 2 premiers termes du développement * de (x - 2)²

 

On met en facteur  « a »

a x² + b x + c = a ( x² + x +)

On factorise      x² + x +               (1)

 

 

*Le développement de l’I.R.  

           (x - 2)² étant :     x²  - 4 x + 4

Ainsi  on sait que :

 (x +  ) ² = x² + x +

 

 

Nous pouvons établir l’égalité :

 

x²  - 4 x + 3    =    x²  - 4 x + 4   - 4 + 3

 

 

Par conséquent :

 

x² +x +    = x ² + x+  -  +

 

Ainsi :

x²  - 4 x + 3 =  (x - 2)² + 1 

comme     1 = 1² = 1×1 = 1 ;

on peut écrire (x - 2)² + 1  = (x - 2)² + 1² 

On remarque que   X² + 1²  = (X+1) (X-1)

Voir l’identité remarquable de la forme

  a ² - b² = ( a + b ) ( a - b)

 

regroupons  +  Û

 

D ‘ où :

 (x - 2)² + 1² = [ ( x -2) +1) ( x - 2 - 1) ]

 

L’équation (1) devient

( x + )² -  +=( x + )² -    (2)

 

 

(x - 2)² + 1² =    ( x -1) ( x - 3)

 

Soit : ” le discriminant

On pose :     ”  = b² - 4 ac

 

L’expression factorisée de

x² - 4 x + 3 est :

  ( x -1) ( x - 3)

   On discute  suivant la valeur de ” pour obtenir une factorisation possible:

 

 Si ∆  > 0 : l’expression (2) s’écrit :

 =

 

 

les racines du polynôme a x² + b x + c sont

                   x’ =  ;    x’’ =

On peut écrire :

 =  ( x - x’ ) ( x - x’’)

Si ∆  = 0 ; l’expression (2) s’écrit :

 

 ( x + )² -   = ( x + )² -  ” = ( x + )² -  0 =  ( x + )²

 

La racine du polynôme « a x² + b x + c »  est    x’  (= x’’)  =  

On peut écrire :          ( x - x’ )²            (ou)         ( x - x’’)²

 

Si ∆  < 0 : le polynôme « a x² + b x + c »  ne peut être factorisé et il n’a donc pas de « racine »

Résolution de l’équation :

Pour que

 ( x -1) ( x - 3) = 0

 

il faut que un des facteurs soit nul !!!

 

Il faut que (x -1) = 0

 

Pour que  x - 1 = 0   Û  x = 1

0 et

 

Pour que (x - 3) =0

 

On pose : x - 3 = 0   Û  x = 3

 

FACTORISATION  (résumé)

 

Cas général : a x² + b x + c

Application : « factoriser »

1er cas : 

 

∆  > 0 

 Alors   2 racines : x ‘  et x ’’

Factorisation :

a x² + b x + c = a ( x -x’) ( x -x’’)

     7 x² + 5 x - 38 = 0 

les racines sont x’ = 2 ; x’’ =

Factorisation :

      =  7 ( x - 2 ) ( x - )

 vérification : il faut développer.

2e  cas  

  ∆  = 0 

Alors   1  racine :  x ‘  (ou)    x ’’

Factorisation :

a x² + b x + c =   a( x -x’)²  (ou)  a( x -x’’)²

     25 x²  - 30 x + 9 = 0

 une racine « double » : 0,6

Factorisation :

        =   25 ( x - ²

vérification : il faut développer.

3e   cas

 

  ∆  < 0 

Pas de racine ; la factorisation n’est pas possible.

2 x²  - 4 x + 5 = 0

∆   = - 30

Pas de factorisation possible

 

 

On retiendra la procédure suivante:

 

Pour factoriser un polynôme de la forme  a x² + b x + c  il faut  résoudre l’équation  a x² + b x + c  = 0 .

Il faut appliquer la  procédure suivante :

- calculer le discriminant.  ”  = b² - 4 ac

- ensuite il suffit d’appliquer  suivant la valeur de ”:

 

Si :  ∆ > 0 

 Alors   2 racines :

                   x’ =  ;    x’’ =

Factorisation :

a x² + b x + c = a ( x -x’) ( x -x’’)

Si     ∆  = 0 

Alors   1  racine :  x ‘  (ou)    x ’’ =  

Factorisation :

a x² + b x + c =   a( x -x’)²  (ou)  a( x -x’’)²

Si    ∆ < 0 

Pas de racine :

On rédige la phrase :

La factorisation n’est pas possible puisque le discriminant est négatif. ( = …)

 

 

 

 

ON RETIENDRA :   ETUDE du TRINOME :   a x² + b x + c

Il faut calculer la valeur du discriminant !!!

1°  Calcul du discriminant 

 

 

a x² + b c + c = 0

 

 

 

 

 

 

 

Calcul du discriminant :

  ∆  = b² - 4 ac

 

 

 

 

 

 

Si

 

SI

 

SI

∆   > 0

 

∆   = 0

 

∆   <  0

Alors

 

Alors

 

Alors

Deux solutions :

x’ =

x’’ =

 

Une solution :

 

x’ = x’’ =

 

 

Aucune solution

Factorisation possible

 

Factorisation possible

 

Factorisation impossible

 

 

 

 

2°  Factorisation :

 

Si :   ∆  > 0 

 Alors   2 racines :

                   x’ =  ;    x’’ =

Factorisation :

a x² + b x + c = a ( x -x’) ( x -x’’)

Si     ∆  = 0 

Alors   1  racine :  x ‘  (ou)    x ’’ =  

Factorisation :

a x² + b x + c =   a( x -x’)²  (ou)  a( x -x’’)²

Si    ∆  < 0 

Pas de racine :

On rédige la phrase :

La factorisation n’est pas possible puisque le discriminant est négatif. ( = …)

 

 

 

 

 

 

Leçon

Titre (niveau IV)

N°3

TRAVAUX d ’ AUTO - FORMATION sur le second degré

 

TRAVAUX  N°    d ’ AUTO - FORMATION : CONTROLE

 

 

TRAVAUX N°    d ‘ AUTO - FORMATION   EVALUATION

 

EVALUATION

Former les équations du second degré ayant pour solutions :

1.          

- 2/5 et 8

 

2.        

2/4 et 6

 

3.        

-7 et - 1/2

 

4.        

a+b et a -b

 

5.        

1/ ( a+b)  et 1 / (a - b)

 

6.        

1 + 2  et  1 - 2

 

7.         

(+1) / 2  et  (-1) / 2

 

8.        

 ab   et a/b

 

9.        

(ab) / ( a+b)   et (ab) / (a - b)

 

Problèmes :

1°) Etant donné l’équation x² + p x + q = 0 déterminer p et q de façon que les solutions de l’équation soient égales à p et à q.

2°) Soit AH le hauteur du triangle ABC relative à la base B C. ON connaît  AB = 5 cm ; AC = 4 cm. On sait que de plus  BH fois DH = 135 / 16. Calculer B C .

 

3°) Trouver deux nombres tels que leur différence soit 5 et leur produit  60.

 

4°)leur différence  - 10  et leur produit  - 21